Анализ формы: новый метод исследования сигналов

ПРЫГУНОВ А. И. проф., докт. техн. наук, зав. кафедрой технической механики Мурманского государственного технического университета Alexander.Prygunov@mstu.edu.ru

Работа посвящена обоснованию и изложению нового метода исследования нестационарных сигналов. Метод основан на получении безразмерной меры сходства локальной формы исследуемого сигнала с формой-эталоном в виде синусоиды определённой частоты путём использования алгоритмов время-частотного анализа высокого разрешения и методов частичной реконструкции сигнала в фазовом пространстве. Приведены примеры использования метода в различных областях техники и технологии. Метод может быть использован также для анализа образов на наличие периодических структур волнового типа.

Введение   

                Традиционные методы анализа физически реализованных сигналов, образов и временных рядов, порождаемых сложными (полимодальными) динамическими системами, в основном базируются на статистических методах, чаще всего на спектрально-корреляционных методах в различных их вариантах [1,2,3,4]. При этом, вследствие статистического подхода к анализу сигналов динамическая сущность процессов их порождающих, как правило, уходит на второй план. И только динамический подход к анализу сложных систем характерный для современной нелинейной динамики позволяет рассматривать анализ сигналов как процесс идентификации динамических систем по результатам анализа экспериментальных данных [5,6].

                Если рассмотреть динамическую систему в виде системы дифференциальных уравнений вида L y(t) = f(t) , где L – линейный дифференциальный оператор, становится очевидным, что физически реализуемыми решениями этой системы могут быть либо периодические моды, либо апериодические экспоненты, так как только эти функции порождают себе подобные производные. В том и другом случае могут порождаться как устойчивые, так и неустойчивые решения. В случае характерных динамических решений типа периодических мод речь следует вести преимущественно о структурной устойчивости, проявляющейся в локальной устойчивости к малым возмущениям топологической структуры фазовой траектории, соответствующей решению. В случае характерных для кинетики апериодических решений преимущественно  следует говорить об устойчивости по Ляпунову. При этом, в глобальном плане неустойчивости соответствует режим инфинитного разбегания фазовой траектории решения, физически соответствующий разрушению системы (например, кинетика взрыва), а устойчивости постепенное затухание движений. Известно, что основным параметром, определяющим вариант решения, является вязкость (сопротивление) в системе. Обычно, апериодические решения кинетического типа характерны для систем с высоким демпфированием и характеризуют процессы относительно медленного развития.

                Важной особенностью поведения сложных динамических систем является существенная нестационарность вплоть до хаотичности порождаемых ими сигналов. Традиционный спектральный анализ на базе быстрого преобразования Фурье (БПФ) не эффективен для нестационарных сигналов с временным масштабом нестационарности много меньшим продолжительности подлежащей анализу реализации. Это связано с усреднением мощности флуктуаций при спектральном анализе (спектр мощности) по всему времени наблюдения сигнала. Наиболее очевидным путём применения БПФ к анализу нестационарных сигналов является разбиение реализации на отдельные короткие равно длинные участки с последующим применением алгоритма БПФ к каждому из них. Этот приём широко известен в практике анализа сигналов как БПФ на коротких реализациях (Short Time Fast Fourier Transform или STFFT).

                Математическим основанием для подобного подхода к анализу сигналов является широко известный метод решения линейных уравнений динамики, известный как метод функций Грина, заключающийся в решении уравнений для физически реализуемых динамических систем в виде свёртки

,

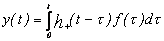где h₊ (t - t) есть частный случай функции Грина и представляет собой нормальную реакцию системы на единичный импульс: L h₊(t - t)=d₊ (t - t). Метод функций Грина представляет собой наиболее адекватный эксперименту метод решения дифференциальных уравнений, так как сводит процедуру их решения к свёртке произвольного внешнего воздействия на систему на импульсный отклик. Довольно часто в экспериментальных исследованиях идентификация динамических систем бывает связана с необходимостью тестового, например, импульсного воздействия на систему. Ясно, что алгоритм STFFT в обобщённом понимании может рассматриваться как отражение метода функций Грина применительно к анализу сигналов, так как он, по сути, основан на расчёте локальной свёртки сигнала на гармонику определённой частоты, которая при небольшом демпфировании в системе может рассматриваться как  вариант отклика периодического типа на импульсное воздействие.

                Отличительной особенностью анализа на коротких реализациях является необходимость применения сглаживающих окон. Как известно, без них усиливается влияние эффекта растекания дискретных составляющих в боковые лепестки. Кроме того, увеличение числа участков разбиения исходной реализации ограничивает разрешающую способность анализа во временной области, поэтому в настоящее время предложен ряд алгоритмов анализа со скользящими сглаживающими и взвешивающими (усредняющими) окнами. Нами предложен вариант время-частотного анализа со сглаживающим окном, частично выполняющим функцию взвешивающего окна.

1. Время - частотный анализ: декомпозиция по всплескам

                Наиболее известными вариантами время-частотного анализа высокого разрешения являются наиболее ранний анализ со скользящим гауссовским окном (окно Габора) [7] и наиболее развитый и эффективный вариант анализа этого типа известный как распределение Вигнера-Вилли (WVD). [8]. Применение алгоритмов анализа со скользящими окнами позволяет существенно увеличить разрешающую способность анализа во временной области при сохранении достаточно высокого разрешения в частотной области, однако сопряжено со значительным увеличением объёма вычислений. Рассмотренные методы анализа широко применяются при углублённом анализе сигналов во время-частотной области, например при распознавании речи. В настоящее время показано [9,10], что декомпозиция сигнала под скользящими окнами является частным случаем декомпозиции сигнала (образа) в новом типе ортогонального базиса известного как базис всплесков (wavelet basis).  Мы так же пошли по пути разработки скользящего окна с требуемыми свойствами на основе теории всплесков.

                По своей сути базис всплесков представляет собой ортогональный базис разложения функций в функциональном гильбертовом пространстве, элементы которого определяются параметрами  a, b и задаются выражением

                                        Y_a,b = p ^-1/4| a | ^-1/2 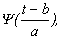                               (1)

где Y(t)-производящая или материнская функция.

В качестве производящей функции можно использовать её основной вариант, известный как функция Морле, которую можно записать в виде:

                                                Y = e ^{i 2pf0  êt ê} e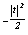,                                         (2)

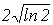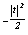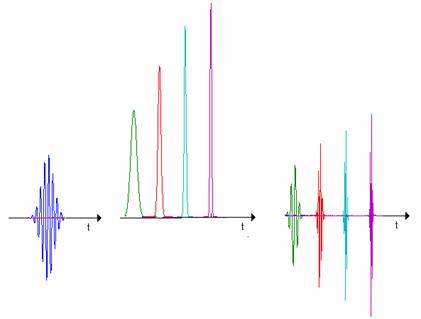
где f₀ =1/ Гц » 0,6 Гц , t - время в с.  Анализ функции (2) показывает, что она представляет собой гармонику с частотой f₀ под окном e ^. Форма этого окна близка к форме окна Габора (гауссовский колокольчик). На рис. 1а приведён качественный вид реальной части функции (2), который и называют всплеском. Следует отметить, что выбор значения f₀ задаёт соотношение между эффективной шириной окна и периодом анализируемой гармоники. В нашем случае эффективная ширина окна во временной области принята равной периоду анализируемой гармоники, что соответствует максимальной разрешающей способности анализа по времени.

 

                                            

                Если принять значение параметра шкалы a = 2 ^{- j/B} и параметра временной локализации b = 2 ^{- j/B} k, где j, k - натуральные числа; B-число полос анализа приходящихся на октаву, то выражение для коэффи­циентов декомпозиции сигнала x(t) в базисе Y_a,b (Y _jk ) примет вид:

                                           w_jk = ò dt x(t)Y^*_jk(t),                                           

где

Y _jk (t)= p ^{-1 / 4} 2 ^{j / 2B}exp{- h²(2 ^{j / B} n - k) ²/ 2}exp(i 2pf0 h ê2 ^{j / B} n - k ê),  или

                                            w_jb = ò dt x(t)Y^*_jb(t),                                           (3)

где

Y_j,b = p ^{-1 / 4} 2 ^{j / 2B} exp{-2 ^{2j / B} h²(n - b) ²/ 2} exp(i 2pf0 2 ^{j / B} hê n - b ê),         (4)

где B-число полос, прихо­дящихся на одну октаву; n и b- целые числа, соответствующие текущему номеру отсчёта на реализации и номеру отсчёта, соответствующему максимуму окна короткой волны на реализации, соответственно; звездочка означает процедуру комплексного сопряжения. Анализ выражений (3), (4) показывает, что декомпозиция по всплескам при соответствующем выборе

                                                  j =B log₂(f / f₀)                                               (5)

становится аналогичной преобразованию Фурье на коротких реализациях со специфическим нелинейным в смысле зависимости от частоты усредняющим окном

                                g_j,b= p ^{-1 / 4} 2 ^{j / 2B} exp{-2 ^{2 j / B} h²(n - b) ²/ 2}.                     (6)

В этом и заключается суть отличия предложенной декомпозиции от традиционного преобразования Фурье на коротких реализациях. Изменение геометрии окна при фиксированной позиции во времени (b=const) позволяет как бы всматриваться в сигнал по частоте в темпе октавы или её кратностей.

                Отличительной особенностью анализа в базисе всплесков является его высокая чувствительность к кратковременным высокочастотным флуктуациям сигнала, так как окно всплеска обеспечивает адекватную оценку таких флуктуаций за счёт одновременного увеличения амплитуды окна при уменьшении его ширины. В этой связи следует отметить, что в связи с анализом в базисе всплесков часто упоминают принцип неопределённости Гейзенберга. 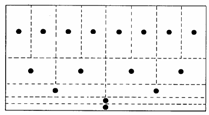Разрешающая способность анализа во временной области возрастает с ростом частоты. В этом заключается принципиальное отличие  анализа в базисе всплесков (рис. 2а) от преобразования Фурье на коротких реализациях (рис. 2б), при котором разрешающая способность анализа по времени не зависит от частоты  и связана только с разрешающей способностью анализа в частотной области, абсолютное значение которой не зависит от частоты.

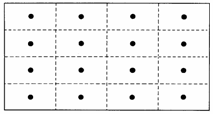
Решётки (frames) дискретных состояний (j,b) в зависимости от типа преобразования ( j – по вертикали, b – по горизонтали)

Рассмотрим вариант октавного анализа (B=1) в диапазоне частот до 10кГц. Пусть длина реализации t_н= 5 с, интервал между отсчётами в соответствии с теоремой Найквиста h = 50 мкс, тогда мощность реализации Q=10⁵  отсчётов,  j_min = 1,  j_max = j = log₂(10000 / 0,6)»14. Записанное в конечных разностях соотношение (3) с учётом (4) при B=1 приводит к выражению для коэффициентов разложения

                           w_jb = 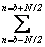h x(n)g_j,b exp(i 2pf0 2 ^{j / B} hê n - b ê),                          (7)

где N-часть реализации Q , находящаяся под окном (4).

Разрешающая способность анализа во времени зависит от частоты (от параметра j, так же называемого “шкалой”) в соответствии с выражением      Db_j= 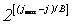. Так, для j=14 Db=1  или 50 мкс, при j=1 Db=2¹³=8192 или 410 мс, поэтому для максимальной частоты (10 кГц) мы должны рассчитать 10⁵ коэффициентов на реализацию, а для минимальной частоты (0,6 кГц) —  лишь 11 коэффициентов на реализацию (рис. 2а).

                Из рассмотренного примера ясно, почему анализ в базисе всплесков называют “частотным микроскопом”. Даже в октавном варианте он обеспечивает высокую чувствительность к высокочастотным флуктуациям сигнала при одновременно высоком разрешении их во времени.

                В то же время, анализ имеет малую разрешающую способность по частоте. Так, j=14 соответствует частота f » 10 кГц, а j=13 уже соответствует частота f » 5 кГц. Если высокочастотная флуктуация имеет определённую частоту (узкополосная флуктуация) с частотой, не совпадающей с частотами указанными выше, мы получим заниженную оценку амплитуды флуктуации.  К счастью, для сложных динамических систем в основном характерны широкополосные высокочастотные флуктуации, что делает это замечание по отношению к ним несущественным.

Опыт работы с преобразованием (3), (4) привёл к выводу о том, что в большинстве случаев для оценки эволюции мод  во времени достаточно проведения анализа для основной и трёх высших гармоник  анализируемой моды. Это достигается при уже при 1/3-октавном анализе в базисе всплесков. В дальнейшем мы покажем, что ограничение числа высших гармоник анализа имеет более глубокие основания и связано с процедурой реконструкции фазового пространства сигнала по методу вложения (embedding procedure). Номер треть-октавной полосы, соответствующей основной гармонике колебания найдём из соотношения

                                               j =int[B log₂(f / f₀)],                                             (8)

которое отличается от соотношения (5) тем, что здесь подчёркнута необходимость выделения целой части из соотношения (5). В свою очередь, выделение целой части (округление в меньшую сторону) приводит к тому, что частоты под второй экспонентой выражения (4) могут существенно отклоняются от истинных частот гармоник.  Поэтому для анализа сигналов мы предлагаем использовать преобразование

                                 w_jl,b = 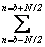h x(n)g_jl,b exp(i 2plf hê n - b ê),                     (9)

где f- частота основной гармоники; l - номер гармоники;  N-часть реализации Q, находящаяся под окном (6), определяется, исходя из принятого значимого отклонения от нуля функции окна, асимптотически стремящейся к нулю на бесконечности. В частности, мы принимаем N из условия

                                             g_j1,b |_n=N/2 < 0,01 g_j1,b |_n=b .                                       (10)

При этом, для обеспечения адекватной сравнительной оценки мощности основной и высших гармоник на временном интервале, сравнимом с основным периодом число элементов N, находящихся под окном остаётся неизменным и для более узких окон, соответствующих высшим гармоникам.

Анализ выражения (9) показывает, что в таком виде анализ может рассматриваться как разновидность время - частотного анализа со скользящим окном (6), обладающим нелинейными свойствами всплеска. При этом настройка окна полосовая (треть-октавная), а настройка частоты анализа точная. Для фиксированного значения b коэффициенты разложения для основной гармоники w_j1,b  и трёх высших гармоник w_j2,b , w_j3,b , w_j4,b могут быть найдены из выражения (9) при j₁ = int{B[log₂ (f/f₀)]}» int[3(log₂ f)+2,2]; j₂= j₁+3; j₃= j₁+5; j₄= j₁+6, где f-  частота основной гармоники. Время на выполнение такого расчёта на несколько порядков меньше, чем время на расчёт (7). На рис. 1б приведены функции окна для четырёх гармоник (основной и трёх высших), на рис. 1в приведены соответствующие всплески, мерой корреляции сигнала, с которыми в текущий момент времени являются коэффициенты w_jl,b. В этом принципиальное отличие анализа по всплескам  от Фурье анализа.                                                                                              

а	б
Рис.3

 

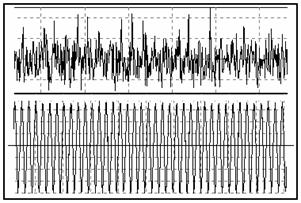
Если в случае цифрового Фурье анализа коэффициенты Фурье должны рассматриваться как мера корреляции сигнала с соответствующей не локализованной во времени гармоникой (рис. 3а), то в случае анализа в базисе всплесков, речь идёт о мере корреляции с соответствующими локализованными во времени всплесками (рис. 3б). Рассмотрим примеры применения анализа в базисе всплесков к исследованиям динамики машин.  

                1.1. Центробежный насос с признаками кавитации.

                Пример иллюстрирует высокую эффективность анализа в области предельных (преднайквистовых) частот.

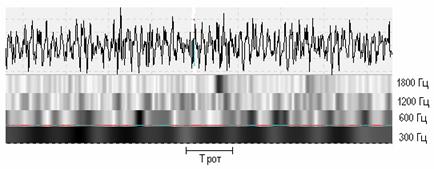
Рис. 4

                На рис. 4 приведены результаты анализа виброускорения центробежного насоса с признаками кавитации. В качестве частоты анализа принята лопастная частота 300 Гц и её высшие гармоники. Частота Найквиста для рассматриваемой реализации 2000 Гц. Очевидна достаточная стабильность лопастной частоты (заметны небольшие изменения уровня с частотой вращения).  Однако, вибрация на частоте 1800 Гц, характеризующая кавитацию, носит явно нестационарный характер. Отмечено два кавитационных хлопка на фазе работы одной-двух лопастей. Интервал времени между хлопками примерно равен двум периодам вращения ротора насоса. Высокая разрешающая способность анализа во времени позволяет подробно проанализировать динамику развития кавитационных хлопков. Очевидно, что анализ в полосе 1800 Гц может быть эффективным методом диагностики отрывной кавитации в насосе уже на ранних стадиях её зарождения. Никакой другой метод не обеспечивает такой эффективности время-частотного анализа на предельных частотах. 

               

1.2. Судовой двигатель внутреннего сгорания

                Поршневые машины характеризуются фазово детермированной динамикой, поэтому анализ их вибрации наиболее целесообразно проводить во время-частотной области с фазовым селектированием. На рис. 5 приведены результаты анализа в базисе всплесков виброускорения цилиндровой втулки крупного судового дизеля (6ЧРН 52,5/72). Собственная частота колебаний втулки 360 Гц, поэтому анализ проведён именно для этой частоты. Собственная частота возбуждена на достаточно коротких фазовых интервалах, что является хорошей иллюстрацией необходимости повышения разрешающей способности анализа во времени в ряде практических приложений. В моменты вспышки уровни высших гармоник так же высоки, что свидетельствует о существенном отклонении формы колебаний в этот фазовый момент от синусоиды собственной частоты. Однако, в области низких цилиндровых давлений имеется ряд импульсов малой амплитуды близких к чистому тону на частоте 360 Гц, что привело к выводу о возможности разработки на базе время-частотного анализа с предложенным окном принципиально нового метода анализа, основанного не на амплитудно-частотном анализе, а на поиске в сигнале моментов возбуждения чистых мод совершенной тональной формы, с целью оценки с высоким разрешением эволюции во времени не только амплитуды, но и формы сигнала.

 

Рис. 5

 

2. Анализ формы: метод и его обоснование

 

          Как отмечалось выше, большинство сигналов, генерируемых сложными динамическими системами, являются полимодальными сигналами, поэтому их динамический анализ базируется на разработке процедур позволяющих снижать модальность сложного сигнала путём выделения наиболее существенных мод, число которых определяет динамическую размерность процесса. Основанием для такого подхода является теорема Такенса [5], которая утверждает, что путём правильного подбора размерности m и параметра задержки t можно получить (m+1)–мерный фазовый образ достаточно полно отражающий свойства истиной траектории динамической системы в фазовом пространстве. Уравнение этой синтетической траектории может быть записано в виде

                                                              z_i+1 = x (t - it),                                       (11)

где индекс (i +1) суть номер координаты реконструированного фазового пространства Z={z₁,...,z_i+1}, а параметр i принимает целочисленные значения от 0 до m. В экспериментальных исследованиях динамики данная процедура называется вложением кратности m, а получаемый фазовый образ (11) - картой задержки. Утверждается, что размерность сложных процессов обычно находится в пределах от m= 3 до m= 6. Таким образом, размерность соответствующих фазовых образов от 4 до 7.

                При проведении процедуры вложения важным параметром является задержка t , которая не обязательно должна быть равна интервалу отсчёта. Чаще всего её выбирают, исходя из ожидаемого или оценённого, например, по методу авторегрессии, периода одной из главных мод процесса. При этом наилучшее раскрытие траектории в проекции {z₁,z₂}, наблюдается при значениях задержки близких к четверти этого периода. В тоже время, при таком выборе задержки в проекции {z₁,z₃} фазовый образ выродится в максимально компактную линию. Поэтому сам выбор параметра задержки с последующим анализом проекций получаемого результата вложения может рассматриваться как разновидность частотного анализа исходного сигнала. Ограничению гармонического анализа четвёртой гармоникой основной анализируемой частоты соответствует пятимерный фазовый образ {z₁,...,z₅}, который в свою очередь соответствует размерности исходного процесса m =4. Таким образом, предложенное нами ограничение время-частотного анализа четвёртой гармоникой позволяет, тем не менее, анализировать достаточно сложные динамические процессы. Следует отметить, что относительные количественные меры анализа сигналов, основанные на исследовании плоских проекций фазовой траектории весьма чувствительны к малым изменениям частотного состава спектра сигнала. В свою очередь, частотный состав спектра сигнала характеризует совершенство формы волны процесса, соответствие её форме идеальной синусоиды.  Достаточно вспомнить широко используемое в практической электротехнике понятие о коэффициенте нелинейных искажений в сети. Поэтому на основе анализа плоских проекций фазовых траекторий возможно получение высокочувствительных относительных количественных мер, характеризующих фазово-локальную форму сигнала.

                Для перехода от результатов время-частотного анализа во время-фазовую область нами предложено синтезировать текущую фазовую траекторию так же с помощью процедуры вложения, но с известными априори параметрами t и m. Первым шагом на основе четырёх известных текущих коэффициентов разложения сигнала в базисе всплесков генерируется текущая четырёхмодальная модель сигнала

             x_b(t)= w_j1,b  cos(W t)+ w_j2,b cos(2W t)+ w_j3,b cos(3W t)+ w_j4,b cos(4W t),    (12)

для которой при каждом фиксированном b строится соответствующая фазовая траектория в соответствии с (11) при t = 0,5(p /W ). Дальнейшему анализу подвергается проекция {z₁,z₂}, исходя из того, что в случае совершенной локальной формы сигнала (синусоида с основной частотой время-частотного анализа) эта проекция должна быть окружностью на периоде T=2p /W . Мерой сходства формы сигнала с совершенной формой предложено считать отношение площади A, заметаемой радиусом вектором точки на фазовой траектории в проекции {z₁,z₂} за период Т, к площади круга с диаметром D

                 k_f =4A/pD²,  где 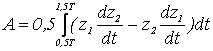; D = x_bMAX - x_bMIN .       (13)

Эту безразмерную относительную меру k_f предложено называть коэффициентом формы сигнала. Следует отметить, что текущее значение коэффициента формы может быть рассчитано для каждого b. Таким образом, мы получаем отображение исходного сигнала в область, которую можно назвать областью “форма-время” и обозначить как {k_f (b)} или k_f (t). Соответствующие кривые можно условно назвать формограммами. Рассмотрим применение анализа на ряде простейших примеров.

2.1. Анализ синусоид и их гармоник

                На рис. 6 представлены результаты анализа формы для модельного сигнала, состоящего из четырёх последовательных участков, соответствующих основной частоте и трём высшим гармоникам. Как и следовало ожидать, коэффициент формы для колебаний с основной частотой равен (1,0), для колебаний

Рис. 6

с частотой второй и четвёртой высших гармоник он равен (0,0) и для колебаний с частотой третьей гармоники равен (–3,0).  Последний результат связан с тем, что при анализе частоты в три раза меньшей основной частоты фазовая траектория синтезированного сигнала (12) успевает совершить три полных оборота в противоположном относительно основной частоты направлении за период Т. Таким образом, возбуждение третьей гармоники в сигнале может сопровождаться существенным уменьшением коэффициента формы вплоть до отрицательных значений.

                Обращает на себя внимание факт уменьшения интенсивности спектральной составляющей время-частотного анализа с ростом частоты сигнала, несмотря на увеличение с ростом частоты амплитуды окна (9) (см. рис.1б). Это связано с тем, что рост амплитуды окна лишь частично компенсирует его сужение, сопровождающееся ростом разрешающей способности по времени. Поэтому, энергетические оценки вклада в форму сигнала его высокочастотных компонент в соответствии с решёткой, изображённой на рис. 2а, не будут слишком завышенными.

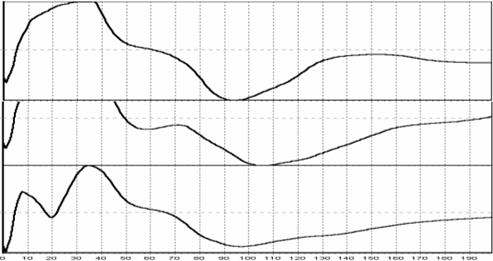
Рис. 7

                Для того, чтобы более подробно исследовать влияние на результаты анализа формы изменений характера анализируемого сигнала нами было предложено проводить расчёт коэффициента формы для широкого диапазона значений установленной частоты (периода) анализа. При достаточном разрешении по периоду можно получить образ, который соответствует зависимости коэффициента формы от частоты анализа при неизменной позиции окна во времени. Этот образ условно может быть назван текущим спектром формы сигнала в заданный момент времени. На рис. 7 результаты анализа спектра формы для сигнала в виде чистой синусоиды и при наличии её высших гармоник.

                На рисунке сверху вниз представлены три спектра формы: для сигнала в виде чистой синусоиды, для сигнала в виде комбинации синусоиды и её второй гармоники и для сигнала в виде комбинации синусоиды и её третьей гармоники. Видно, что при анализе чистой синусоиды положительный максимум коэффициента формы достигается при значении периода 34, соответствующему периоду синусоиды. В тоже время, отмечается отрицательный минимум спектра при периоде примерно в три раза превышающем основной. Наличие отрицательных минимумов спектра формы является важным признаком наличия в сигнале формы синусоид с периодом в три раза меньшим периода минимума. Наличие в сигнале второй гармоники приводит к незначительному росту коэффициента формы на периоде второй гармоники равному 17 и к появлению дополнительного локального минимума на периоде в полтора раза превышающему основной (область периода 50). Наличие в сигнале третьей гармоники приводит к формированию локального максимума на её периоде равном  9, но не сопровождается появлением дополнительного локального минимума, так как он должен приходиться на область основного периода и поэтому проявляется лишь в виде снижения значения коэффициента формы на основном периоде.

                2.2. Анализ ударно-импульсного сигнала

                На рис. 8 представлены результаты анализа ударно-импульсного сигнала с выраженным откликом периодического типа. В данном случае рассматривается сигнал, генерируемый стальным шариком, падавшим с некоторой высоты на обрезиненную подложку. Всего зарегистрирован один импульс от удара и четыре импульса от подскока шарика. Из рисунка видно, что значение коэффициента формы не зависит от амплитуды сигнала, так как, несмотря на уменьшение амплитуды колебаний подложки, форма колебаний остаётся в высокой степени гармонической. В тоже время импульсы от удара и подскоков генерируют характерный для импульсных сигналов полигармонический спектр, что приводит к локальному уменьшению коэффициента формы в основном за счёт возбуждения третьей гармоники собственной частоты.

Рис. 8

                На данном примере видно, почему отрицательное значение приобретаемое коэффициентом формы при наличии в сигнале третьей гармоники может быть выгодно при анализе. Все четыре импульса от отскоков в ходе анализа уверенно зафиксированы. Поэтому локальное снижение значения коэффициента формы вплоть до отрицательных значений чаще всего свидетельствует о наличии локального импульса в сигнале. Коэффициент формы в рассматриваемом примере сохраняет своё максимальное значение при уменьшении амплитуды сигнала в процессе затухания вплоть до уровня шума. Уровень шума в эксперименте был примерно на 40 дБ ниже максимального уровня сигнала. Из примера видно существенное отличие предлагаемого метода анализа от традиционных амплитудно-частотных методов, заключающееся в том, что амплитуда (энергия) становится несущественной по сравнению с формой. Даже малому сигналу совершенной формы по результатам анализа соответствует максимальное значение коэффициента формы.

3. Исследование вибрации машин, вибродиагностика

                При исследованиях вибрации машин мы имеем дело с анализом физически реализованных решений для относительно простых динамических систем направленным на идентификацию изменений их параметров по результатам эксперимента. Исходя из логики получения решений, основанных на методе функций Грина, изменение параметров системы должно в полной мере отражаться в изменении отклика её на внешнее импульсное воздействие. Поэтому, несмотря на сложность анализа нестационарных сигналов, периодические ударные воздействия, характерные для машин с ударно-импульсной динамикой, способны исполнить роль высокочувствительного тестового воздействия, содержащего большой объём информации об эволюции параметров системы. Для успеха при этом необходимо иметь два условия: возможность высокого разрешение анализа во времени и возможность реализации относительных оценок отклика. На самом деле эти два условия взаимосвязаны, так как с увеличением разрешения во времени неизбежно возникает проблема адекватности абсолютных амплитудных оценок (проблема взвешивания). Анализ формы лишён этого недостатка, так как коэффициент формы является высокочувствительной относительной оценкой изменения частоты и формы отклика и не требует оценки его абсолютной величины.  Последнее обстоятельство значительно облегчает использование метода в автоматизированных системах контроля, так как  приводит к исключению процедур метрологической аттестации и поверки измерительной аппаратуры. Дополнительным основанием к использованию метода для целей вибродиагностики является прогнозируемая чувствительность результатов анализа к зарождающимся дефектам, так как изменение формы сигнала не требует в отличие от изменения амплитуды существенных энергетических затрат. По сути, данный подход в вибродиагностике зарождающихся дефектов не является оригинальным. Так, в работах ИМАШ РАН неоднократно использовалось понятие о векторе в условном n – мерном пространстве [11,12]. При этом координатами пространства являлись абсолютные значения вибрации на характерной вынужденной или собственной частоте и на её гармониках. Очевидно, что изменению соотношения между амплитудами гармоник соответствует изменение формы сигнала в нашем понимании. Одним из важнейших типов машин с ударно-импульсной динамикой являются двигатели внутреннего сгорания, поэтому применение метода рассмотрим на примере этих машин.

                3.1. Исследование процессов с низким давлением в цилиндрах ДВС

                На рис. 9 представлены результаты анализа формы для колебаний цилиндровых втулок среднеоборотного судового дизеля 6 ЧРН 52,5/72 на частоте, соответствующей собственной частоте колебаний втулки 320 Гц на фазовом интервале, соответствующем двум циклам цилиндров. При этом, представлены втулки выполненные из разных материалов. Верхняя формограмма соответствует чугунной цилиндровой втулке, нижняя – цилиндровой втулке выполненной из биметалла «сталь-чугун» по технологии МГТУ [13]. В нижней части рисунка представлены также фазы открытия выпускных и впускных клапанов дизеля.

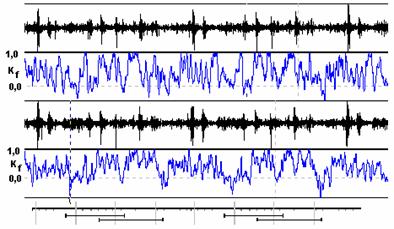
Рис. 9

наибольших значений не только на фазах, соответствующих рабочему ходу поршня (от вспышки до открытия выпускных клапанов), но и на фазах продувки цилиндра (от открытия выпускных до закрытия впускных клапанов). При этом фазовым моментам открытия и закрытия клапанов, сопровождающихся импульсным изменением давления в цилиндре, соответствуют локальные уменьшения коэффициента формы вплоть до отрицательных его значений.

                Из рисунка очевиден периодический характер формограмм и качественное соответствие между их характером в аналогичные фазовые моменты для разных цилиндров. Так, на формограммах отчётливо проявляется фазовый момент перекладки поршня в верхней мёртвой точке на стадии продувки с выраженным тональным откликом втулки на него. Обращает на себя внимание периодический по фазе характер формограмм после вспышки, особенно для чугунной втулки. При этом период  процесса изменения коэффициента формы на фазе рабочего хода соответствует относительно низкой частоте порядка десятков герц. В этой связи следует отметить, что до настоящего времени в теории динамических процессов, протекающих в ДВС, дискутируется вопрос о возможности наличия низкочастотных волн давления газов в цилиндрах на фазе рабочего хода дизеля. Возможно, рассматриваемая особенность является проявлением этих гипотетических волн. В тоже время, на формограммах виден и ряд отличий. Так, отклик на импульсное воздействие слоистой втулки, для которой характерно внутреннее трение между слоями, имеет явно демпфированный характер, что проявляется в незначительном снижении значений коэффициента формы на отклике, к отклонению его формы от чистого тона. Следует отметить, что до применения анализа формы методами абсолютной виброметрии и спектрального и обычного время-частотного анализа существенных отличий в вибрации этих втулок отмечено не было.

                Таким образом, показано, что анализ формы может быть высокочувствительным методом анализа вибрационных процессов в ДВС. На основе его путём последовательного фазового усреднения формограмм можно по аналогии с индикаторной диаграммой получить диаграмму чувствительную не только к процессам высокого давления, протекающим в цилиндре, но и к процессам низкого давления, таким, например, как работа клапанов, перекладки в цилиндропоршневой группе. Исследуя формограммы для частот, характерных для других узлов ДВС, таких как форсунки, рамовые и мотылёвые подшипники, штоки клапанов, можно получать информацию об их состоянии возможно даже только на основе расчёта среднего эффективного значения коэффициента формы на цикле работы машины. Следует вновь подчеркнуть, что изменение формы сигнала не связано однозначно с изменением его энергии, что является основанием для прогнозируемой высокой чувствительности метода к зарождающимся дефектам не способным существенно повлиять на энергию процесса.

                3.2. Исследование резонансных режимов в механизмах

                Одной из причин усталостного разрушения зубчатых передач и подшипников, входящих в состав приводов механизмов газораспределения дизелей является нелинейный субгармонический резонанс, возникающий в зацеплении под влиянием импульсного характера нагрузки топливных насосов высокого давления (ТНВД). В работе [14] показано, что для резонанса характерна выраженная анизотропия вибрации по направлениям и частота в два раза меньшая частоты зацепления. На рисунке 10 показаны результаты анализа формы колебаний на частоте  резонанса, полученные на цапфе промежуточной шестерни привода ТНВД судового дизеля 6ЧРН 52.5/72 в радиальном и продольном направлениях.

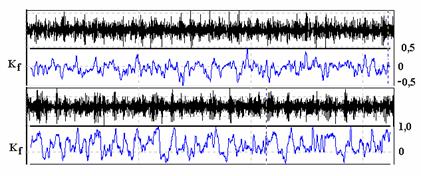
Рис. 10

                Из рисунка видно, что среднее значение коэффициента формы для вертикального направления (верхняя формограмма) близко к нулю, в то время как среднее значение коэффициента формы для продольного направления (нижняя формограмма) составляет 0,53. Таким образом, из примера видно, что возникновение и развитие резонанса в области привода ТНВД может контролироваться и нормироваться, исходя только из расчёта среднего значения коэффициента формы, что удобно использовать при разработке автоматизированной системы диагностики данного вида дефектов. Детальное рассмотрение формограмм с учётом возможности фазовой привязки позволяет определить топливные насосы, на фазе работы которых наблюдается наибольшее развитие резонанса, что позволяет дать конкретные технологические рекомендации по устранению дефекта путём регулировки зазоров и биений в зацеплении на фазе работы соответствующих плунжеров.

                В качестве ещё одного примера исследования резонанса в машинах рассмотрим пример влияния крутильного резонанса на продольную вибрацию валогенератора рыбопромыслового судна. На рисунке 11 представлена виброграмма и результаты её анализа во время - частотной области с использованием

Рис. 11

обычного алгоритма быстрого преобразования Фурье на коротких реализациях. Как видно из рисунка сигнал носит нестационарный характер. При этом можно выделить два типа текущих спектров. Тип А с преимущественным возбуждением основной частоты вынуждающего воздействия (около 50 Гц), и тип Б с дополнительным возбуждением более низкочастотных неустойчивых колебаний в частотном диапазоне от 25Гц до 50 Гц (низкая разрешающая способность анализа по частоте не позволяет сделать более точной оценки).

Результаты анализа спектра формы для виброграмм этих двух типов приведены на рисунке 12.

Рис. 12

                Для участков виброграммы типа А (верхняя часть рисунка) характерен спектр гармонического типа с основным периодом  22 мс (частота  46 Гц), для участков виброграммы типа Б (нижняя часть рисунка) также характерен спектр гармонического типа с периодом 31 мс, что соответствует частоте 33 Гц, совпадающей с собственной частотой крутильных колебаний вала.

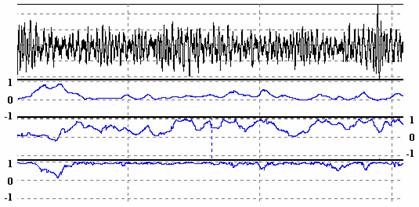
Рис. 13

                На рисунке 13 приведены формограммы для выявленных частот и дополнительно для субгармоники 1/2 основной частоты вынуждающего воздействия (23 Гц). Из рисунка видно, что основной формой колебательного процесса является синусоида с частотой вынуждающей силы (нижняя формограмма). При этом форма, соответствующая форме вынуждающего воздействия, наблюдается почти без изменений на всём протяжении сигнала. Исключение составляют лишь кратковременные моменты преимущественного развития субгармонических колебаний (верхняя формограмма), являющихся следствием нелинейной упругости соединительной муфты при скачках нагрузки. Наряду с формой вынуждающего воздействия на участках виброграммы типа Б наблюдается также форма, соответствующая собственным крутильным колебаниям (средняя формограмма). Таким образом, исходная виброграмма может рассматриваться как результат взаимодействия нелинейных вынужденных и близких к ним по частоте собственных крутильных колебаний в системе. При этом степень проявления формы собственных колебаний в сигнале определяется соотношением между мгновенной энергией вынуждающего воздействия и энергией крутильных колебаний. При недостаточной энергии основного вынуждающего воздействия интенсивные крутильные колебания вблизи резонанса могут рассматриваться как дополнительное вынуждающее воздействие при исследовании продольной и поперечной вибрации агрегатов.

                3.3. Оценка перспектив использования метода в диагностике машин

                Метод открывает новые возможности акустической диагностики машин и конструкций, базирующихся на его основных достоинствах, к которым относятся:

-          высокая чувствительность к проявлению в сигнале синусоподобных волн малой амплитуды и длительности;

-          высокая чувствительность к малым отклонениям формы колебаний от совершенной формы вне зависимости от изменения их амплитуды (энергии);

-          относительный характер контролируемого параметра (коэффициента формы).

                Эти достоинства приводят к тому, что появляется возможность, используя измерительные тракты для вибрации и воздушного шума, не требующие калибровки и метрологического освидетельствования, разрабатывать методики и приборы, позволяющие диагностировать зарождающиеся дефекты машин и конструкций, элементы которых подвергаются ударно-импульсному воздействию. При этом ударно-импульсный характер динамики машин может быть как естественным, например, для машин с возвратно-поступательными кинематическими парами, так и связанным с проявлением различного рода аномалий, как в машинах роторного типа. Селективность диагностики обеспечивается наличием характерного набора частот импульсного отклика для конкретных деталей и узлов конкретных машин. Перспективно использование метода для контроля характерных для нелинейной динамики нестационарных резонансных режимов, включая полимодальные резонансные режимы.

                Впервые открывается возможность построения эффективных алгоритмов аналитической формализации опыта диагностики практических механиков, основанного на субъективных определениях нестационарных акустических процессов типа: узел «стучит», «звенит», «скрипит», «скрежещет». Можно рекомендовать проводить процедуру такой формализации в следующей последовательности:

-          нестационарные акустические сигналы от дефектного и бездефектного, по мнению эксперта, узла исследуется на наличие ударных импульсов и квазигармонических всплесков;

-          в области всплесков и импульсов анализируется спектр формы сигналов с учётом рекомендаций раздела 2.1.;

-          проводится анализ сигналов в области «форма-время» для частот, выявленных по результатам анализа спектра формы;

-          на основе анализа формограмм вырабатываются диагностические признаки, в качестве которых могут использоваться максимальные, средние, средние квадратичные, усреднённые по фазе и другие статистические значения коэффициента формы, для дефектного и бездефектного состояний.

Следует отметить, что в ряде случаев значение частоты анализа может быть получено, исходя из теоретических расчётов ожидаемых собственных частот и частот резонансов.  

4. Исследование медленных технологических процессов

          При исследованиях динамики технических систем довольно часто кроме анализа быстропеременных сигналов возникает необходимость анализа нестационарного поведения медленно меняющихся параметров технологических процессов таких, как температура, давление, мощность, ток, напряжение и т.д. Характерные масштабы нестационарности этих параметров во времени составляют минуты, и даже часы. Рассмотрим пример применения анализа формы к исследованию нестационарного поведения одного из основных параметров технологического процесса бурения нефтяных скважин – давления бурового раствора, измеренного на манифолде скважины.

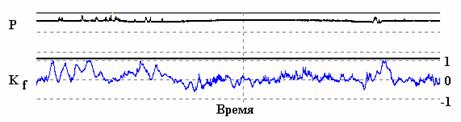
Рис. 14

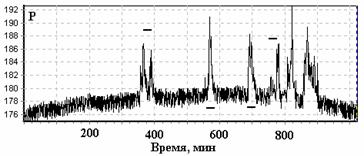
                На рисунке 14 представлен характер изменения давления в устьевой части скважины за время около 60 часов с интервалом 1 мин. Обращает на себя внимание наличие кратковременных бросков давления, в пределах 10% его среднего значения, в начале и в конце реализации.

                Существует предположение, что эти броски давления в буровом растворе могут быть связаны с выбросом в скважину пластового флюида. Если это предположение верно, то анализируя динамику давления в области бросков, возможно получить признак входа бурового инструмента в производительные пласты, что является основной целью контроля состояния забоя, так как определяет необходимые изменения технологии бурения, связанные с обеспечением безопасности ведения буровых работ.

Рис. 15

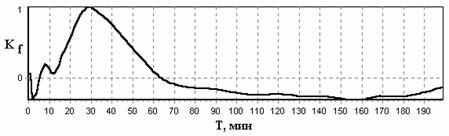
                На рисунке 15 представлен спектр формы, полученный в области одного из бросков давления, из которого следует, что основной частотой квазигармонических флуктуаций давления в области броска является частота 0,62 мГц, соответствующая периоду 27 мин, поэтому нами была получена формограмма для этой частоты, представленная в нижней части рис. 14. Из формограммы следует, что в проявлению бросков давления соответствуют области увеличения значения коэффициента формы на частоте 0,62 мГц вплоть до максимальных его значений. Рассмотрим возможные причины такого характера изменений формограммы.

Рис. 16

                На рисунке 16 более подробно представлена зависимость давления от времени за первые 15 часов наблюдений. Видно, что минимальная длительность выбросов и интервала их чередования соответствует периоду 27 минут (горизонтальные отрезки на рисунке). Поэтому факт увеличения коэффициента формы сигнала для этого периода в области наблюдения выбросов является признаком примерного равенства временного масштаба выбросов и кратности периодов их чередования. Такая картина может быть следствием промежуточного накопления пластового флюида в коллекторах ограниченной ёмкости, какими являются полости скважины, с последующим его высвобождением по типу медленного барботажа бурового раствора пластовым флюидом. Следует отметить, что для такой модели с увеличением интенсивности поступления флюида из пласта, продолжительность выбросов давления при неизменном объёме внутрискважинных коллекторов должна уменьшаться, при этом число выбросов должно возрастать. Таким образом, текущий анализ формы сигнала давления на манифолде, может быть достаточно эффективным методом контроля над процессом выброса пластового флюида в скважину.

Заключение

           Предложен новый метод анализа нестационарных сигналов, отличающийся высокой разрешающей способностью во времени при сохранении достаточного частотного разрешения. Отличительной особенностью анализа является его независимость от изменений амплитудных характеристик сигналов, что позволяет использовать метод для контроля над первоначальными изменениями на стадии их зарождения. Метод оказывается одинаково эффективным при использовании для сигналов различной природы и сложности. Эта универсальность обусловлена тем, что в основе метода лежат наиболее общие принципы исследования динамики сложных, как правило, нелинейных процессов. Рассмотренные в работе примеры демонстрируют высокую эффективность применения метода к решению конкретных прикладных задач, что позволяет надеяться на создание нового класса методов акустической диагностики машин по нестационарным сигналам. Автор открыт для сотрудничества со специалистами, располагающими данными по направленным диагностическим экспериментам с поршневыми машинами возможно через Internet.

Литература

1. Бендат Дж., Пирсол А. Применение корреляционного и спектрального анализа. - М.: Мир, 1983, 312с.

2. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. - М.: Мир, 1989. - 448 с.

3. Артоболевский И.И., Бобровницкий Ю.И., Генкин М.Д. Введение в акустическую динамику машин. - М.: Наука, 1979. -296с.

4. Измерение, обработка и анализ быстропеременных процессов в машинах / В. П. Максимов, И. В. Егоров, В. А. Карасёв. — М.: Машиностроение, 1987. — 208с.

5. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. – М.: Эдиториал УРСС, 2000. – 336с.

6. Doyle J. F. A wavelet deconvolution method for impact force identification // Experimental Mechanics. - 1997. -V.37. -№4. - P. 403-408.

7. Gabor D. Theory of communication // J. Inst. Elect. Eng. (London). - 1946. - V.93. - №3. - P. 429-457.

8. Claassen T. A. C. M., Mecklenbrauker W. F. G. The Wigner distribution - a tool for time-frequency signal analysis // Philips J. Res. - 1980. - V.35, - P. 217-250, 276-300, 372-389.

9. Daubechies I. The wavelet transform, time-frequency localisation and signal analysis // IEEE Trans. Inform. Theory. -1990. - V.36. - №5. - P. 961-1004.

10. Mallat S. G. A theory for multiresolution signal decomposition: the wavelet representation // IEEE Trans. on Pattern Analysis and Machine Intelligence. - 1989. - V.

11. Генкин М. Д., Соколова А. Г. Виброакустическая диагностика машин и механизмов. - М.: Машиностроение, 1987. - 288с.

12. Виброакустическая диагностика зарождающихся дефектов /Ф.Я.Балицкий, М.А.Иванова, А.Г.Соколова, Е.И.Хомяков. - М.: Наука, 1984. - 119с.

13. Папуша А.Н., Прыгунов А. И. Собственные колебания одно- и многослойных цилиндровых втулок ДВС // Двигателестроение. - 1990. -№9. - С. 9-12.

14. Прыгунов А. И., Папуша А. Н. Нелинейные резонансы механических систем как диагностические признаки // Cб. материалов 9-ой Межвузовской школы-семинара “Методы и средства технической диагностики”, книга 2. - Ивано-Франковск, Облполиграфиздат, 1990. - С. 43-49.