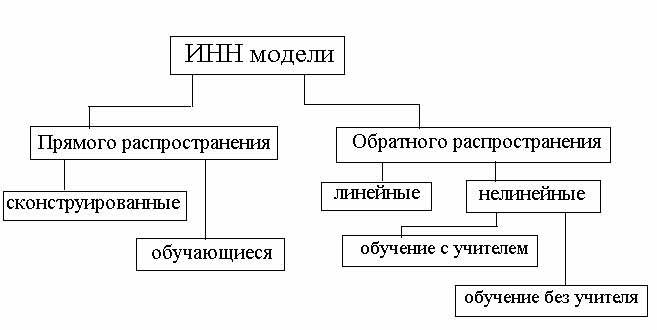
Рисунок 1. Общая классификация моделей ИНС
Краткий обзор. Искусственная Нейронная Сеть (ИНС) - функциональная имитация упрощенной модели биологических нейронов и ее цель – сконструировать пользовательские ‘компьютеры’ для реально-мировых проблем и воспроизведите интеллектуальные методы оценок данных подобно распознаванию образов, классификация и обобщение, используя простые, распространенные и ясные единицы обработки, названные искусственными нейронами. ИНС – мелко-уровневая параллель выполнения нелинейной, статико-динамической системы. Сведения ИНС и их способность разрешить тяжелые проблемы появились в значительной степени из-за связности, которою предоставляет нейроны, а это большие вычислительные способности, обусловленные их параллельно распространяемой структурой. Поток распространения интереса к ИНС, во многом обусловлен тем, что ИНС алгоритмы и архитектуры могут быть применены в технологии VLSI в задачах реального времени. Число ИНС приложений сильно возросло за последние несколько лет, подогреваемое как теоретическими, так и практическими успехами в разнообразных дисциплинах. Эта статья представляет обзор исследований и развитие многих ИНС приложений. Представлен краткий обзор ИНС теории, модели и приложения. Обсуждаются потенциальные области применения и будущие тенденции.
Ключевые слова: черный ящик, модели нейронных сетей, приложения нейронных сетей
В последние годы было слияние идеи и методологии в различных дисциплинарных областях, что породило чрезвычайно интересную область исследования названную искусственная нейронная сеть (ИНС) [1]. Нейрон – базовый фундаментальный блок нейронной системы, который выполняет вычислительные и коммуникационные функции. ИНС - функциональная имитация упрощенной модели биологических нейронов и ее цель – воспроизвести интеллектуальные методы оценок данных подобно распознаванию образов, классификация и обобщение, используя простые, распространенные и ясные единицы обработки. Для этого обратились к искусственным нейронам или элементам обработки (ОЭ) [2]. Искусственный нейрон был спроектирован, чтобы имитировать перво-порядковые характеристики биологических нейронов. Сведения ИНС и их способность разрешить тяжелые проблемы появились в значительной степени из-за связности, которою предоставляет нейроны, а это большие вычислительные способности, обусловленные их параллельно распространяемой структурой или архитектурой, в которой каждый нейрон выполняет только очень ограниченное действие. Хотя отдельный нейрон работает очень медленно, они могут быстро находить решение, работая параллельно.
Главное преимущество подхода ИНС – это знание проблемной области распространяется через нейроны, и обработка информации осуществляется параллельным методом [3]. ИНС - инструменты параллельной обработки данных, способные к изучению функциональной зависимости данных [2]. Существующие адаптивные единицы могут изучать эти сложные взаимоотношения даже когда никакой функциональной модели не существует. Это свойство обеспечивает создание “черного ящика ” с малой или отсутствующей априорной информацией о функции непосредственно. ИНС - мелко-уровневая параллельная реализация нелинейной статико-динамической системы. Они имеют способность должным образом классифицировать нелинейные взаимоотношения и однажды обучившись, могут классифицировать новые данные намного быстрее, чем при решении с помощью аналитической модели.
Поток распространения интереса к ИНС обусловлен, в значительной степени благодаря появлению мощного, нового метода, так и пригодностью вычислительных возможностей для моделирования. Особенно это связанно с тем, что сегодня, ИНС алгоритмы и архитектуры могут применяться в технологии VLSI для задач реального времени. [4]
В настоящее время, можно выделить два главных направления в ИНС исследованиях. Исследования в первом направлении занимаются моделированием мозга для объяснения его познавательного поведения. С другой стороны, первоначальная цель исследователей во втором направлении - сконструировать полезные ‘компьютеры’ для решения практических проблем распознавания образов рисунком с помощью этих принципов.
Были предложены различные типы нейронных сетей (НС), но все они имеют три общих особенности: отдельный нейрон, связь между ними (архитектура) и алгоритм обучения. Каждый тип ограничивает вид связи, насколько возможно. Например, можно задать, что, если один нейрон соединяется со вторым, то второй нейрон не может иметь другую связь по направлению к первому. Вид возможной связи, общее направление – это архитектура или топология нейронной сети.
Нейронная сеть состоит из одного или больше слоев нейронов. В большом числе моделей НС, как например персептрон, линейный ассоциатор, мульти-слоевая сеть с обратным распространением обучения, машина Boltzmann и модель Grossberg, выходы элементов одного слоя только позволяют активизировать нейроны следующего слоя [5]. Однако в нескольких моделях, как например сети Kohonen и Hopfield моделирующий сигнал позволяет активизировать нейроны в этом же слое. В модели подобной саморганизовывающейся карте (SOFM), сеть соединяет вектор входов с двухразмерной сеткой выходов нейронов [6, 7]. Рисунок 1 показывает общую классификацию моделей ИНС.
Связь между парой нейронов имеет числовое значение названное синоптическим весом или адаптивным коэффициентом [8]. Сила взаимосвязи может быть представлена, как матрица веса с положительным (разрешающим), отрицательным (препятствующим), или нулевым (нет связи) значением [5]. Вес определяет структуру сигнала, который передается от одного нейрона к другому, таким образом, кодируются знания сети. Когда кумулятивное возбуждение превышает кумулятивное сдерживающие значение, названное порогом, обычно это значение 40 mV, выходы нейронов пересылают сигналы далее к другим нейронам. [9] Только некоторые сети обеспечивают мгновенный ответ. Другим сетям нужно время, чтобы ответить и они характеризуется их временным поведением, на которое мы ссылаемся, как нервную динамику. Временной интервал между входами и выходами сети называется периодом скрытого суммирования.

Рисунок 1. Общая классификация моделей ИНС
Говорят, что нейрон «обучаем», если его порог и входной вес изменяемы. Входы подаются на нейроны. Если нейроны не предоставляют желаемый выход (определяется нами), значит, это свидетельствует об ошибке. Необходимо, несколько весов и порогов изменить, чтобы компенсировать ошибку. Правила, которые определяют, как точно эти изменения должны происходить называются алгоритмом обучения. Алгоритмы обучения отличаются формулировкой способа регулирования синаптического веса нейрона.
Вес сети постепенно в течение некоторого времени регулируется для улучшения предопределенного критерия качества работы. Процесс обучения лучше всего рассматривать, как “поиск” в многомерном весовом пространстве для решения, которое постепенно оптимизирует предварительно указанную функцию. НС накапливает знание о задаче после каждой итерации процесса обучения.
Для того чтобы сеть изучала одну потребность, подайте ряд примеров на рассмотрение сети, чьи свойства известны или представляют неизвестную модель [2]. Набор предоставленных примеров называется учебным набором или учебными образцами.
После периода обучения, сеть должна быть способна выдавать правильный выход для любого вида входа. Это называется тестированием. Если сеть не была обучена для этого входа, то она должна попробовать предоставить корректный выход в зависимости от того, как она была обучена. Это называется обобщением. Актуальный метод определения выхода для предоставленного набора входов называется алгоритм обработки [2]. Различные НС характеризуется разницей в архитектуре, алгоритмом обучения, алгоритмом обработки.
Каждый алгоритм обучения содержит основное обучающее правило. Есть два главных правила, предназначенных для обучения: правило Hebbian для обучения с учителем и правило Delta для обучения без учителя. Адаптация их простыми модификациями для удовлетворения специфических контекстов производится во многих других правилах обучения. Обучение с учителем требует соединения каждого входного вектора с целевым вектором, представляющим желательный выход, вместе они образуют учебные пары [10]. Желательный выход представляет оптимальное действие, которое выполняет НС. [8] Обучение с учителем НС возможно для сетей с прямого распространения для таких как многослойный персептрон, функционально связанная сеть, радиальная сеть функции основания, параллельная однородно-организованная иерархическая нейронная сеть, или для сети обратного распространения как, например сеть Hopfield. Обучение без учителя не требует целевых векторов для выходов. Обучающий алгоритм изменяет веса сети в ответ входам, которые последовательно производят вектор выходов. Kohonen’s SOFM и адаптивная резонансная теория – примеры обучения без учителя НС.
В отличие от экспертных систем, НС не являются явным набором правил, которые представляют правильное соответствие выхода входу (вход-выходная картография). Способность учиться на примерах - характеристика ИНС. Поэтому они могут изменить свое поведение в соответствии внешним данным. На рисунке 2 изображен искусственный нейрон. Вход нейрона может идти от актуальных внешних данных или от других нейронов. Его выход может питаться от других нейронов или непосредственно из внешней среды [2]. OUT (выход нейрона) получается с помощью суммы весов входов [NET (сеть вход к нейрону) или комбинационная функция (векторно-скалярная функция)] преобразованной функцией преобразования F [также называемой активационной функцией (скаляр-в- скаляр функцией)]. Эта функция преобразования вносит нелинейность в систему. Это делает систему более мощной.
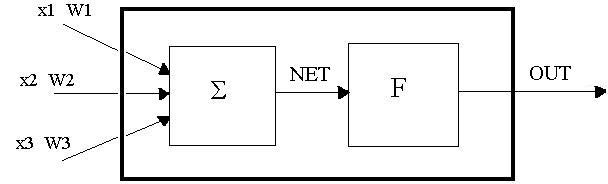
Рисунок 2. Искусственный нейрон
Сетевой вход к i-му нейрону формируется по формуле:
NETi=X 1 W1+ X 2 W2 +…+ X n Wn
NETi=ΣX i Wi
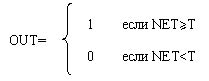
Выход i-го нейрона соответствует формуле:
OUTi=F(NETi)
Начиная с их появления, ИНС нашли много применений во многих из областей. Таблица 1.показывает основные приложения различных ИНС моделей в хронологическом порядке. Ниже представлены некоторые применения из всего множества, описанного в литературе.
Обработка сигналов
В критических положениях, инженеры должны быстро оценивать различные способы решения и осуществлять оптимальное корректирующее действие. Однако, в реальном времени число сообщений (сигналов), полученные на VDU слишком велико, учитывая время, доступное для их оценки. Ценность оперативной помощи – в обработки таких сигналов в масштабах реального времени и приведение в готовность оператора для идентифицирования причин наиболее важных из этих сигналов. ИНС были применены для такой обработки сигналов. Chan [11] предложил трехслойную сеть персептрона для этих целей, с обещанием результатов моделирований. Быстрый ответ обученной ИНС и ее способность обобщать становятся наиболее полезным в этом приложении.
Таблица 1. Основные применения различных моделей ИНС
| Область применения | Год |
| Распознавание машинописных символов | 1957 |
| Устройства подавления эха в телефонных линиях | 1960 |
| Распознавание речи | 1967 |
| Синтез речи | 1974 |
| Извлечение знаний из баз данных | 1977 |
| Распознавание рукописных символов | 1978 |
| Радар и сонар идентификация | 1978 |
| Авиационная навигация | 1980 |
| Обработка изображений | 1982 |
| Ассоциативная память | 1985 |
| Оценка заявлений на кредит | 1986 |
Вихревой текущий анализ
Анализ вихревых текущих потерь требует числового решения интегрально-дифференциальных уравнений. Разделение этих уравнений и решение их с использованием метода конечных разностей вычислительно очень дорого. Feria и другие [12] описал клеточную ИНС которая дает более быстрый, вычислительно менее дорогой и более простой метод решения этих уравнений. Они предложили клеточную НС, как альтернативу методу конечных разностей. Клеточную сеть симулировали, используя SPICE. Клеточная сеть вычислила вихревые потоки и вихревой поток потери в исходном текущем проводнике переноса в переменном магнитное поле. Эта реализация открывает широкий ряд применений в структурном анализе, электромагнитном вычислении полей, и т.п.
Контроль гармонических источников
Hartana и Richards [29, 30] описали идентификацию и контроль гармонических источников в системах, содержащих нелинейную нагрузку. Это подход содержит в себе достаточно прямое измерение гармоник в системе. Эти авторы применяют многоразовый трехслойный персептрон. ИНС были обучены, с использованием результатов моделирования для различных условий нагрузки. ИНС были использованы в союзе с основной формулой оценки в точке и контролировали источник гармоник. Этот подход смог идентифицировать гармонический источник, который не был идентифицирован ранее.
Применение в атомных электростанциях
В проекте, инициированном Американским департаментом энергетики, исследователи университета Теннеси изучали потенциальное применение ИНС для увеличения безопасности и эффективности атомные электростанции [15, 16, 17]. Областью исследования было: диагноз специфики анормальных условий, обнаружение изменения метода действий операций, сигнальное предупреждение, мониторинг проверки клапанов, моделируя термодинамики станции, контроль параметров станции, анализа вибрации станции, и т.п.
ИНС имеет способность развиваться, обобщая решение проблемы, кроме этого используют обучение, чтобы производить действительные решения, даже, когда есть ошибки в учебном наборе. Эти факторы объединяют, чтобы сделать НС мощным инструментом для моделирования проблем, в которых функциональные отношения точно не определены или изменяются с прохождением времени.
Другая область, которой может быть выгодно, использовать НС - те, где время, требуемое для генерации решения критическое как, например приложения, требующие многих решений в быстрой последовательности. Способность НС производить быстро решения независимо от сложности проблемы делает их ценными даже, когда доступны альтернативные методы, способные производить решения более точно.
[2] В контрасте к классическим методам или экспертным системам, которые пытаются формализовать знание и развивают частную качественную модель системы, ИНС не обеспечивают формальное представление отношения между входными и выходными данными. Поэтому необходимо проверить работа ИНС статистическими испытаниями.
Каждый вид НС при проектировании пытается охватить определенный класс проблем. Будем надеяться, что на некоторой стадии мы сможем комбинировать все типы НС в общепринятой структуре. Будем также надеяться, что мы достигнем нашей цели объединить мозг и компьютер.
По существу ИНС - часть искусственного интеллекта (AI). Успех был в моделировании интеллекта. Поэтому, ИНС, возможно, становится основой для большинства интеллектуальных систем. Начиная с ИНС, которые могут рассматриваться, как инструмент “низкоуровневой” обработки данных, гибридные подходы, которые комбинируют ИНС с другими методами, такими как экспертные системами, нечеткой логикой и генетическими алгоритмами, многообещающая область исследования. В настоящее время, интеграция нечеткой логики с ИНС - главная область исследования, комбинирующая преимущества обоих областей [18]. Генетические алгоритмы все более применяются в проектах ИНС, как например топология и оптимизация параметра.
[1] S. K. Joshi, “Steady state security monitoring of power system using neural nets,” International Conf. on computer applications in electrical engineering, recent advances, pp. 694-696, 8-11 Sept, 1997.
[2] Task force 38-06-06 of study committee 38, “Artificial neural networks for power systems,” Electra No.159, pp. 78-101, April 1995.
[3] Narendranath Udapa A., D. Thukaram and K. Parthasarathy, “An ANN based approach for voltage stability assessment,” International Conf. on computer applications in electrical engineering, recent advances, pp. 666-670, 8-11 Sept. 1997.
[4] Vidya Sagar S. Vankayala and Nutakki D. Rao, “Artificial neural networks and their applications to power systems- a bibliographical survey,” Electrical Power Systems Research, vol.28, pp. 67-77, 1993.
[5] T S Dillon, “Artificial neural network applications to power systems and their relationships to symbolic methods,” Electrical Power & Energy systems, vol 13, pp. 66-72, April 1991.
[6] T. Khanna, Foundations of Neural Networks, Addison-Wesley, Reading, MA, 1990.
[7] J. A. Freeman and D. M. Skapura, Neural Networks: Algorithms, Applications and Programming Techniques, Addison-Wesley, Reading, MA, 1991.
[8] L. Srivastava, S. N. Singh and J. Sharma, “ANN applications in power systems: an overview and key issues,” International lConf. on computer applications in electrical engineering, recent advances, pp. 397-403, 8-11 Sept, 1997.
[9] Yegnanarayana, B., Artificial Neural Network, PHI, New Delhi, 1999.
[10] P. D. Wasserman, Neural Computing: Theory and Practice, Van Nostrand Reinhood, New York, 1989.
[11] E. H. Chan, “Applications of neural network computing in intelligent arm processing,” Proc. IEEE PICA Conf., pp. 246-251, Seattle, WA, USA, 1989.
[12] Y. J. Feria, J.D. McPherson and D.J. Rolling, “Cellular neural networks for eddy current problems,” IEEE Trans. Power Delivery, vol 6, pp. 187-191, 1991.
[13] R. K. Hartana and G. G. Richards, “Constrained neural network based identification of harmonic sources,” Conf. IEEE IAS annual meeting, pp. 1743-1748, 1990.
[14] R. K. Hartana and G. G. Richards, “Harmonic source monitoring and identification using neural networks,” IEEE Trans. on power systems, vol 5, pp. 1098-1104, May 2003.
[15] R. E. Uhrig, “Potential applications of neural networks to nuclear power plants,” Proc. Am. Power conf., vol 53, pp.946-951, 1991.
[16] Y. Izumi and H. Taoka, “Neural networks and its applications to power system,” Electr. Eng. In jpn., vol 109, pp. 230, 1989.
[17] A. Mathur and T. Samad, “Neural networks-a tutorial for the power industry,” Proc. Am. Conf., vol 52, pp. 239-244, 1990.
[18] Manjaree Pandit, laxmi Srivastava and Jaydev Sharma, “Fast voltage contingency selection using fuzzy self-organising hierarchical neural network,” IEEE Trans. on power systems, vol 18, p. 657-664, May 2003.