Прогнозирование пассажирских перевозок на основе обработки временных рядов

В.Г.Дубинина

Источник: http://www.cognitive.ru/innovation/sbornic6/index.htm

В библиотеку

Рассматривается проблема прогнозирования пассажиропотоков, анализируется возможность использования для этих целей временных рядов с явно выраженной сезонной составляющей.

Исследование динамики социально-экономических явлений, выявление и характеристика основной тенденции развития и моделей взаимосвязи дают основание для прогнозирования – определения будущих размеров уровня экономического явления.

В отличие от предприятий, для которых величину конечного продукта можно определить, исходя из наличия сырья и материалов, а также норм расхода этих материалов при производстве конкретных изделий, в любой авиакомпании этот процесс несколько затруднен из-за присутствия субъективного фактора – желания пассажира воспользоваться услугами именно авиакомпании (а не каким-либо другим видом транспорта). Кроме того, на рынке авиаперевозок имеется огромное число авиакомпаний, и за пассажиром остается право выбора. Поэтому для определения объема конечного продукта – пассажиропотока авиакомпании – строится прогноз на будущие периоды[1].

Прогнозирование объемов пассажирских перевозок (как долгосрочное, так и краткосрочное) является для современной авиакомпании одним из аспектов управленческой деятельности. При долгосрочном прогнозировании учитываются тенденции мирового рынка авиаперевозок, которые находят отражение в увеличении или уменьшении частот рейсов на различных направлениях при составлении расписания полетов. Краткосрочное прогнозирование позволяет оперативно отреагировать на изменение ситуации на рынке авиаперевозок и выстроить стратегию авиакомпании, исходя из предполагаемого объема пассажиропотока (например, изменить степень «агрессивности» бронирования, подготовить и провести специальные акции по привлечению пассажиров и т.д.).

Одним из вариантов формирования прогноза объемов пассажирских перевозок является прогнозирование на основе обработки временных рядов, которое позволяет получить весьма надежные результаты [2]. Основой прогнозирования при использовании временных рядов является метод перспективной экстраполяции, которую, однако, надо рассматривать только как начальную стадию построения окончательных прогнозов, т.к. чисто механическое использование экстраполяции может стать причиной значительных ошибок и неправильных выводов.

Применение метода экстраполяции для прогнозирования предполагает, что закономерность, действующая в прошлом, сохранится и в прогнозируемом периоде, но при этом ожидается, что общая тенденция развития перевозок в авиакомпании не должна претерпевать серьезных изменений в будущем (например, параметры расписания должны оставаться относительно стабильными), т.к. теоретической основой распространения тенденции на будущее является свойство инерционности, которое позволяет выявлять сложившиеся взаимосвязи между уровнями временного ряда. Но это справедливо только при построении краткосрочных прогнозов, поскольку за короткий период условия развития явления и характер его динамики не успевают сильно измениться. При долгосрочных прогнозах динамичность процессов вступает в противоречие с инерционностью их развития, поэтому в этих случаях метода экстраполяции недостаточно.

Построение прогнозов является самым последним этапом анализа временных рядов. Общая последовательность этапов анализа временных рядов следующая:

графическое представление и описание поведения ряда;

выделение и исключение регулярных составляющих ряда, зависящих от времени;

подбор математической модели для описания регулярной составляющей и проверка ее адекватности;

прогнозирование будущих значений ряда.

При анализе временных рядов принято выделять две составляющие: регулярную и случайную. Регулярная составляющая в свою очередь включает в себя тренд и сезонную компоненты. Тренд характеризует основную тенденцию развития временного ряда, сезонная компонента определяет колебания, периодически повторяющиеся в некоторое определенное время каждого года. Взаимодействие между собой регулярных составляющих может быть представлено как аддитивная или мультипликативная комбинация:

( аддитивная форма)

( мультипликативная форма)

где Y (t) – значение уровня в момент t,

T (t) – тренд, выбираемый из параметрического семейства,

S (t) – периодическая компонента (сезонная волна),

err – ошибка аппроксимации.

Аддитивная модель характеризуется главным образом тем, что характер сезонных колебаний остается постоянным. В мультипликативной модели характер сезонных флуктуаций остается постоянным только по отношению к тренду и их величина зависит от значений временного ряда.

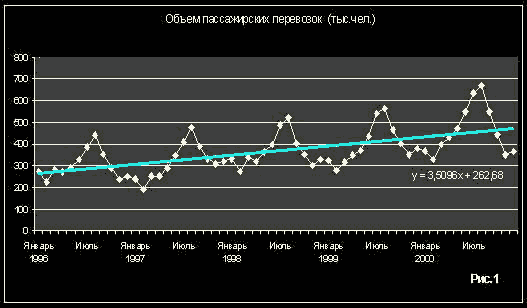
На рис.1 представлены данные об объемах пассажирских перевозок в авиакомпании с 1996 по 2000г. Из графика хорошо видно, что объем пассажиропотока имеет во времени возрастающий тренд и в ряде имеется ежегодно повторяющаяся закономерность – сезонность. Пик перевозок из года в год приходится на август, минимальный пассажиропоток – на февраль. Структура перевозок по месяцам сохраняется каждый год, т.е. период сезонности равен 12.

После того как установлено наличие тенденции, необходимо подобрать уравнение тренда. В нашем случае речь идет о линейном тренде, который описывается следующим уравнением прямой:

,

где – сглаженные (расчетные) уровни исходного временного ряда;

k, b – подлежащие определению зависимые переменные уравнения прямой;

t – независимая переменная ( время ).

Зависимые переменные в уравнении определяются по методу наименьших квадратов из системы уравнений:

,

где Qt – уровни исходного ряда;

t – независимая переменная (время);

n – число уровней ряда.

Решение системы относительно искомых параметров:

и

Упрощенный вариант расчета параметров уравнения заключается в переносе начала координат в середину ряда. При этом упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. При нечетном числе уровней ряда такое преобразование производится следующим образом: t = …, -3, -2, -1, 0, 1, 2, 3, … При четном – t =…, -5, -3, -1, 1, 3, 5, …

Тогда a t = 0 и система уравнений будет иметь вид:

откуда и .

На рис.1 для исходного временного ряда приведен линейный тренд и его уравнение.

Рис.1 Распределение объемов пассажирских перевозок

Кроме линейного тренда, монотонное возрастание или убывание тренда характеризуют функции: параболическая, степенная, экспоненциальная, логарифмическая линейная, логарифмическая парабола, гиперболическая (для убывающих процессов). Кроме того, для временных рядов, стремящихся к некоторой предельной величине, применяются логистические функции.

Теперь перейдем к определению сезонной волны, которая представляет из себя совокупность сезонных индексов. Наиболее распространенными при определении сезонных индексов методами являются следующие[1]:

Методы, основанные на применении средней арифметической или средней геометрической (метод отношений средних помесячных к средней за период, метод отношений помесячных уровней к средней данного года). При аддитивной форме временного ряда в расчете принимают участие среднее арифметические, при мультипликативной – среднее геометрические.

Методы, основанные на применении аналитического выравнивания (выравнивания по прямой, выравнивание по параболе и экспоненте, выравнивание по ряду Фурье).

Ниже приведены примеры расчетов сезонных волн по методу средней и по методу выравнивания по прямой.

Расчет по методу средней применяется в тех случаях, когда временной ряд не содержит ярко выраженной тенденции в развитии. Сезонные волны вычисляются непосредственно по эмпирическим уровням ряда без их предварительного выравнивания. Рассчитываются по нескольким годам средние значения уровней ряда для каждого месяца ` . Затем по вычисленным помесячным средним уровням определяется общий средний уровень .

Далее рассчитываем по месяцам индексы сезонности:

для аддитивной формы, для мультипликативной формы.

Пример расчета сезонных индексов приведен в табл.1.

Таблица 1

Метод выравнивания по прямой применяется в тех случаях, когда исходный ряд содержит определенную тенденцию в развитии, поэтому перед определением сезонной волны данные должны быть обработаны так, чтобы была выявлена эта тенденция. При использовании метода выравнивания по прямой необходимо выполнить следующие действия:

Вычисляются теоретические уровни ряда в каждый момент времени по соответствующему полиному, характеризующему тренд (в данном примере используется линейный тренд на рис.1, параметры которого определены по методу наименьших квадратов);

Определяется отношение фактических данных ( ) к выравненным данным ( ) для каждого месяца (индекс сезонности по месяцам)

;

Находятся средние из соотношений, рассчитанных по одноименным периодам (индекс сезонности по одноименным периодам)

, где n – число одноименных периодов. Проверка правильности вычисления индексов. Средний индекс сезонности для всех месяцев должен быть равен 1, т.к. сезонные колебания взаимопогашаются в течение года.

В табл. 2 приведены расчеты по методу выравнивания по прямой.

Таблица 2

В табл. 3 приведены окончательные значения мультипликативных сезонных индексов для исходного ряда, полученные после процедуры сглаживания методом скользящих средних.

Таблица 3

На рис. 2 приведен исходный ряд и уравнение тренда после выделения сезонной компоненты.

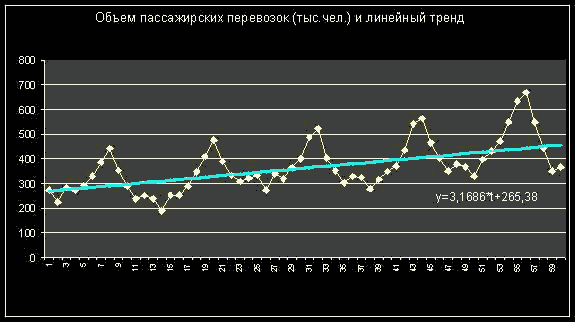
Рис.2 Уравнение тренда без сезонной компоненты

Очевидно, что значения составляющих временного ряда находятся в зависимости от последовательности и методов их выделения.

Если выбранная для прогнозирования кривая не является единственной для описания тенденции, то для каждого уравнения тренда рассчитывается коэффициент детерминации ( R 2), F-критерий Фишера, а также критерий Дарбина-Уотсона. Чем выше R 2, тем выше вероятность того, что временной ряд описывается данным уравнением тренда. Влияние случайного фактора оценивается как (1- R 2). В нашем примере R 2 для линейного уравнения тренда равен 0,9506. Если для описания тенденции исходного ряда использовалась бы парабола, то R 2 равнялся бы 0,9589. Очевидно, что при описании временного ряда предпочтение следует отдавать параболическому тренду.

Критерий Дарбина-Уотсона оценивает автокорреляцию остатков. Если автокорреляция в остатках отсутствует, то уравнение пригодно для прогноза[2].

При выборе уравнения тренда можно использовать среднюю ошибку аппроксимации, которая определяется по формуле:

.

Для нашего примера с линейным трендом средняя ошибка аппроксимации составила 5,5%. Если средняя ошибка не превысила 5-7%, уравнение тренда хорошо подходит для описания тенденции временного ряда.

В приведенном примере при прогнозировании используется сравнительно небольшая глубина исходной статистики. По мере накопления статистической информации вид тренда, используемый для прогнозирования, может изменяться.

Прогнозирование объемов пассажирских перевозок может производиться по различным уровням агрегации данных: как на уровне авиакомпании в целом, так и на уровне отдельных регионов, рейсов и направлений.

Задача прогнозирования объёмов пассажирских перевозок является основой для решения многих задач оптимизации воздушно-транспортной системы по критериям, непосредственно связанным с показателем рентабельности (доходы, затраты, прибыль), поскольку оптимальность планов, получаемых при решении этих задач, зависит прежде всего от точности прогнозов.

Литература:

1. Соколов А.А. “Прогнозирование пассажирских перевозок”. В книге”Наука и техника гражданской авиации”, ВИНИТИ, М, 1975.

2. Правдин Н.Н., Негрей В.Я.” Прогнозирование пассажирских перевозок”, М, Транспорт,1980