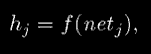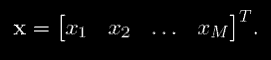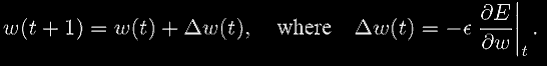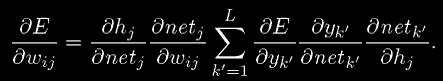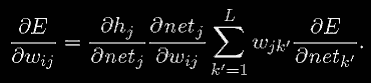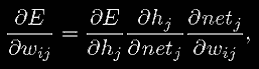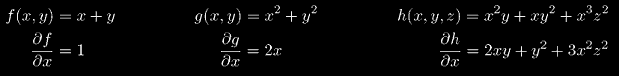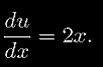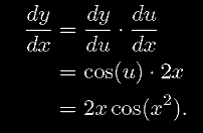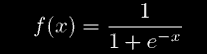Алгоритм обратного распространения
(David McG. Squire, 2000–2004, MONASH UNIVERSITY, Faculty of Information Technology, CSE5230 Data Mining)
Перевод с английского - Корнев С.А.
Оригинал статьи: BackPropHandout.pdf
Источник: http://www.csse.monash.edu.au
Этот документ дает объяснение математического аппарата, применяемого в алгоритме обратного распространения (Rumelhart и др.; 1986). Ключевые математические понятия - частные производные, которые объясняются в приложении A, и цепное правило, которое объясняется в приложении B.
1. Определение сети
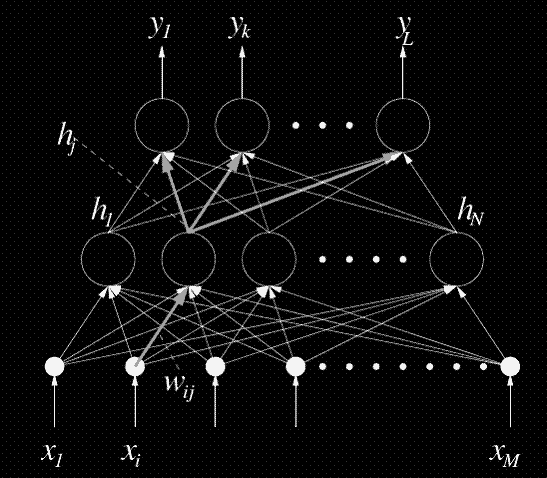
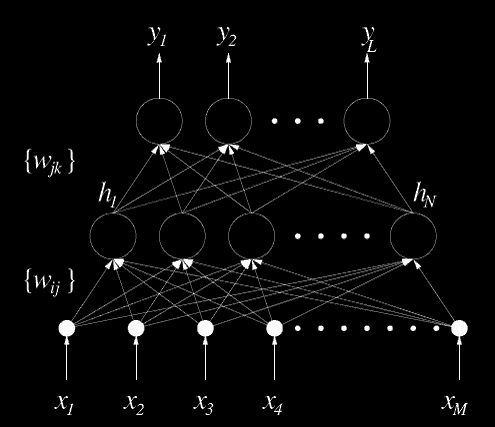
Стандартная нейронная сеть с прямой связью показанная на рисунке 1, также известна как многослойный персептрон (MLP). Обратите внимание, что узлы входного уровня показаны как простые черные круги. Это должно означать, что никакая обработка не происходит в этих узлах: они служат только в качестве входов сети.
 |
Выходной слой
Скрытый слой
Входной слой |
|---|
Рисунок1: Многослойный персептрон: стандартная сеть с прямым распространением
Каждый узел вычисляет взвешенную сумму его входов, и использует ее как входные данные функции преобразования f (). В классическом MLP, функция преобразования - сигмоид.
(1)
Рассмотри узел k в выходном слое. Его выход, yk, представляет
где netk, функция активации, является взвешенной суммой выходов узлов hj в скрытом слое
(2)
Аналогично, выход каждого узла j в скрытом слое:
где
(3)
а xi входы сети.
2. Суммарная квадратичная ошибка и градиентный спуск
Для удобства, мы можем рассмотреть входы сети как входной вектор x, где
Аналогично, выход сети можно рассматривать как вектор выхода y, где
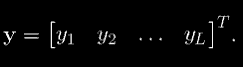
Учебный набор для сети можно представить рядом пар K входных векторов xl и желаемых векторов выхода dl:
Всякий раз, когда входной вектор от учебного набора xl применен к сети, сеть произведет фактический выход yl согласно уравнениям в разделе 1. Мы можем таким образом определить квадратичную ошибку для этого входного вектора, суммируя квадратичные ошибки в каждом узле выхода:
(4)
Параметр 1/2 перед суммой введен только для вычислительного удобства - цель будет состоять в том, чтобы минимизировать ошибку; умножение на константу не имеет никакого значения для этой цели.
Мы можем таким образом определить полную квадратичную ошибку E, суммируя все пары входа-выхода в учебном наборе:
(5)
Наша цель в обучении сети состоит в том, чтобы минимизировать E, находя соответствующий набор весов {{wij}, {wjk}}. Мы сделаем это с использованием алгоритма градиентного спуска: определим, какое направление является "скоростным спуском" на поверхности ошибок и изменим каждый вес w так, чтобы мы двигались в этом направлении. Математически, это означает, что каждый вес w будет изменен на небольшое значение dw в направлении уменьшения E:
Здесь w (t) - вес во время t, и w (t + 1) - обновленный вес. Уравнение 5 называют обобщенным дельта-правилом. Мы видим, что главное в чем мы нуждаемся, чтобы быть в состоянии выполнить градиентный спуск, - частная производная
ошибки каждого веса.
Обобщенное дельта-правило часто дополняют параметром "скачка", который может увеличить скорость обучения и помочь избежать колебаний:
(6)
Величина a определяет эффект, который прошлые изменения веса оказывают на текущее изменение веса. Это известно как "метод тяжелого шара" в числовом анализе.
3. Определение частных производных по весам
3.1 Веса между скрытым и выходным слоями
Начнем с рассмотрения веса wjk между скрытым узлом j и и выходным узлом k. Нам необходимо найти
. Используя цепное правило, мы можем написать
(7)
Уравнение 4 говорит нам что
(8)
Отметим, что взятие частной производной определяет только конкретное значение суммы, где k' = k, так как только выход узла k зависит от wjk. (Сумма по l была опущена для ясности).
Используя уравнение 25, полученное в приложении C на производной сигмоида, мы видим что
(9)
Из уравнения 2, мы получаем
(10)
Заменяя уравнения 8, 9 и 10 в уравнение 7, мы видим что
(11)
Таким образом мы нашли частную производную ошибки E по весу wjk на основе известных переменных и можем использовать этот результат в уравнении 5, чтобы выполнить градиентный спуск для весов {wjk} между скрытым и выходным слоями.
3.2 Веса между входными и скрытыми слоями
Теперь рассмотрим веса wij между входным слоем и скрытым слоем. Снова начнем с уравнения 4 и применим цепное правило для на нахождения выражения для
:
(12)
Отметим, что в этом случае, взятие частной производной не определяет специфический k' из суммы, так как все выходы yk' зависят от wij, как показано на рисунке 2.
Рисунок 2: Все выходы yk зависят от каждого веса wij между входным и скрытым слоями.
Мы уже нашли первые две величины этой суммы в разделе 3.1. Из уравнения 2 мы получаем
(13)
и по аналогии с уравнением 9 мы видим что
(14)
Наконец, используя уравнение 3, мы находим
(15)
Заменяя все эти результаты в уравнение 12, мы получаем желаемый результат:
(16)
Таким образом мы нашли частную производную ошибки E по весу wij на основе известных величин (многие из которых мы уже вычислили при получении
). Вместе с уравнением 11 это дает нам весь
необходимый для того, чтобы уравнение 5 могло использоваться, для выполнения градиентного спуска для всех весов в сети.
4. Почему "Обратное распространение"?
Алгоритм обратного распространения, названный так (Rumelhart; 1986), получил свое название от того факта, что частные производные ошибки по функции активации узлов "распространены назад" через сеть, чтобы была возможность вычислить частные производные для весов на нижних слоях сети. Это становится более ясно, если перезаписать уравнение 12 с величинами, не зависящими от k':
Свертывая один уровень и используя уравнение 13, мы получаем
Замечая что
мы можем записать
(17)
Уравнение 17 показывает нам, что частные производные ошибки по функциям активаций узлов выхода распространены назад через сеть (используя те же веса на соединениях wjk), чтобы разрешить вычисление частных производных ошибки по выходам скрытых узлов. Как только они определены, становится просто найти частные производные ошибки по входным весам этих узлов, используя уравнения 14 и 15.
Важно отметить, что уравнение 17 показывает нам, как частные производные могут быть распространены назад между любой парой слоев: когда
известен в слое, тогда
может быть вычислен для нижнего слоя сети, где {z} - выходы узлов в этом слое. Обратное распространение может таким образом справиться с любым числом слоев. На практике нет необходимости использовать сеть с более чем тремя слоями, так как MLPs с тремя слоями показали, что они являются универсальными аппроксиматорами (Hornik; 1989).
А. Частные производные
Частные производные определены как производные функции множества переменных, когда все переменные кроме представляющей интерес, считаются определенными в процессе дифференцирования (Weisstein; 24 августа 2000).
(18)
Проще всего это понять на примерах. Здесь мы находим частные производные по x, таким образом, другие переменные (здесь y и z) считаются константами:
B. Цепное Правило
Если g(x) дифференцируется в точке x, и f (x) дифференцируется в точке g(x), то f•g дифференцируется в x. Кроме того, пусть y=f (g(x)) и u=g(x), тогда
(19)
Есть множество связанных результатов, которые также называются "цепными правилами" Например, если z=f(x,y), x=g(t), и y=h(t), то
(20)
"Общее" цепное правило относится к двум наборам функций
(21)
и
(22)
Определяя m x n матрицу Якоби как
(23)
и аналогично для
и
получим
(24)
Уравнение 19 также применимо к частным производным, в матричной форме как обозначено уравнением 24.
Более понятно это становится на простых примерах. Рассмотрим функцию
y = sin (x2).
Используя примечание уравнения 19, мы можем записать
y = f (g(x))
где
f (u) = sin(u)
и
g(x) = u = x2.
Тогда мы получим
;
Обьеденив их и используя уравнение 19, мы получаем
C. Производная сигмоида
Исследуя уравнение 1 мы видим что
поэтому
(25)
Это особенно удобно в вычислительном отношении, что производная f (x) может быть выражена исключительно в переменных самой f (x), так как они обычно уже известны.