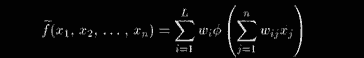Обучение, применение и эффективность нейронных сетей

Источник: Круглов В.В., Дли М.И, ФИЗМАТЛИТ (Издательство Физико-математической литературы), 2001, стр.60-62,78-80,100-102.

В библиотеку

Обучение нейронных сетей

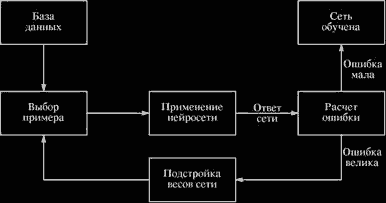
Обучить нейросеть — значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка ал­фавиту. Показав ребенку изображение буквы «А», мы спрашиваем его: «Какая это буква?» Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: «Это буква А». Ребенок запоминает этот пример вместе с верным ответом, т.е. в его памяти происходят некоторые изменения в нужном напра­влении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все буквы будут твердо запомнены. Такой процесс называют «обучение с учителем» (рис. 2.7).

При обучении сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв).

Рис. 2.7. Иллюстрация процесса обучения НС

Предъявляя изображение буквы «А» на вход сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ — в данном случае нам хотелось бы, чтобы на выходе с меткой «А» уро­вень сигнала был максимален. Обычно в качестве желаемого вы­хода в задаче классификации берут набор (1, 0, 0,...), где 1 стоит на выходе с меткой «А», а 0 — на всех остальных выходах. Вы­числяя разность между желаемым ответом и реальным ответом сети, мы получаем (для букв русского алфавита) 33 числа — век­тор ошибки. Алгоритм обучения — это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять сети много раз. В этом смысле обучение скорее напоминает повторение упражне­ний в спорте — тренировку.

Оказывается, что после многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что «сеть выучила все примеры», «сеть обучена», или «сеть натренирована». В программных реализациях можно видеть, что в процессе обучения функция ошибки (например, сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда функ­ция ошибки достигает нуля или приемлемого малого уровня, тре­нировку останавливают, а полученную сеть считают натрениро­ванной и готовой к применению на новых данных.

Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обуче­ния сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описы­вают данную задачу. Так, например, бессмысленно использовать сеть для предсказания финансового кризиса, если в обучающей вы­борке кризисов не представлено. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров.

Математически процесс обучения можно описать следующим образом.

В процессе функционирования нейронная сеть формирует вы­ходной сигнал Y в соответствии с входным сигналом X, реализуя некоторую функцию Y = G ( X ). Если архитектура сети задана, то вид функции G определяется значениями синаптических весов и смещений сети.

Пусть решением некоторой задачи является функция Y = = F ( X ), заданная парами входных-выходных данных ( X 1, Y 1 ), ( X 2, Y 2 ),..., ( X N, Y N ), для которых Y fc = F ( X fc ) ( k = 1, 2,....... TV ).

Обучение состоит в поиске (синтезе) функции G, близкой к F в смысле некоторой функции ошибки Е (см. рис. 2.7).

Если выбраны множество обучающих примеров — пар ( X k, Y k ) (где k = 1, 2,..., TV ) и способ вычисления функции ошибки Е, то обучение нейронной сети превращается в задачу многомерной оптимизации, имеющую очень большую размерность, при этом, поскольку функция Е может иметь произвольный вид, обучение в общем случае — многоэкстремальная невыпуклая задача оптими­зации.

Для решения этой задачи могут быть использованы следующие (итерационные) алгоритмы:

• алгоритмы локальной оптимизации с вычислением частных производных первого порядка;

• алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка;

• стохастические алгоритмы оптимизации;

• алгоритмы глобальной оптимизации.

К первой группе относятся: градиентный алгоритм (метод ско­рейшего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряжен­ных градиентов; методы, учитывающие направление антигради­ента на нескольких шагах алгоритма.

Ко второй группе относятся: метод Ньютона, методы оптими­зации с разреженными матрицами Гессе, квазиньютоновские ме­тоды, метод Гаусса-Ньютона, метод Левенберга-Марквардта и др.

Стохастическими методами являются: поиск в случайном на­правлении, имитация отжига, метод Монте-Карло (численный ме­тод статистических испытаний).

Задачи глобальной оптимизации решаются с помощью пере­бора значений переменных, от которых зависит целевая функция (функция ошибки Е).

Применение нейросети

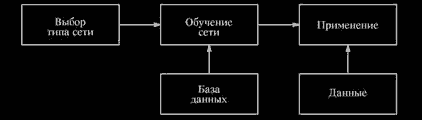
После того как сеть обучена, мы можем применять ее для ре­шения различных задач (рис. 2.14).

Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно

Рис. 2.14. Этапы нейросетевого проекта

действовать и в тех ситуациях, в которых он не бывал в процессе обучения. Например, мы можем читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейросеть, грамот­ным образом обученная, может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Напри­мер, мы можем нарисовать букву «А» другим почерком, а затем предложить нашей сети классифицировать новое изображение.

Веса обученной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на пра­вильный ответ и для нового варианта изображения.

Области применения нейросетей: классифика­ция. Отметим, что задачи классификации (типа распознавания букв) очень плохо алгоритмизуются. Если в случае распознавания букв верный ответ очевиден для нас заранее, то в более сложных практических задачах обученная нейросеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос.

Примером такой задачи служит медицинская диагностика, где сеть может учитывать большое количество числовых параметров (энцефалограмма, давление, вес и т.д.). Конечно, «мнение» сети в этом случае нельзя считать окончательным. Классификация пред­приятий по степени их перспективности — это уже привычный способ использования нейросетей в практике западных компаний (деление компаний на перспективные и убыточные). При этом сеть также использует множество экономических показателей, слож­ным образом связанных между собой.

Нейросетевой подход особенно эффективен в задачах эксперт­ной оценки по той причине, что он сочетает в себе способность компьютера к обработке чисел и способность мозга к обобщению и распознаванию. Говорят, что у хорошего врача способность к рас­познаванию в своей области столь велика, что он может провести приблизительную диагностику уже по внешнему виду пациента. Можно согласиться также, что опытный трейдер чувствует напра­вление движения рынка по виду графика. Однако в первом случае все факторы наглядны, т.е. характеристики пациента мгновенно воспринимаются мозгом как «бледное лицо», «блеск в глазах» и т.д. Во втором же случае учитывается только один фактор, по­казанный на графике, — курс за определенный период времени. Нейросеть позволяет обрабатывать огромное количество факторов (до нескольких тысяч), независимо от их наглядности, — это уни­версальный «хороший врач», который может поставить свой диа­гноз в любой области.

Кластеризация и поиск зависимостей. Помимо за­дач классификации, нейросети широко используются для поиска зависимостей в данных и кластеризации.

Например, нейросеть на основе методики МГУА (метод груп­пового учета аргументов) позволяет на основе обучающей выборки построить зависимость одного параметра от других в виде поли­нома. Такая сеть может не только мгновенно выучить таблицу умножения, но и найти сложные скрытые зависимости в данных (например, финансовых), которые не обнаруживаются стандарт­ными статистическими методами.

Кластеризация — это разбиение набора примеров на несколько компактных областей (кластеров), причем число кластеров зара­нее неизвестно. Кластеризация позволяет представить неоднород­ные данные в более наглядном виде и использовать далее для ис­следования каждого кластера различные методы. Например, та­ким образом можно быстро выявить фальсифицированные стра­ховые случаи или недобросовестные предприятия.

Прогнозирование. Задачи прогнозирования особенно важ­ны для практики, в частности, для финансовых приложений, по­этому поясним способы применения нейросетей в этой области бо­лее подробно.

Рассмотрим практическую задачу, ответ в которой неочеви­ден, — задачу прогнозирования курса акций на 1 день вперед.

Пусть у нас имеется база данных, содержащая значения курса за последние 300 дней. Простейший вариант в данном случае — попытаться построить прогноз завтрашней цены на основе кур­сов за последние несколько дней. Понятно, что прогнозирующая сеть должна иметь всего один выход и столько входов, сколько предыдущих значений мы хотим использовать для прогноза — например, 4 последних значения. Составить обучающий пример очень просто: входными значениями будут курсы за 4 последо­вательных дня, а желаемым выходом — известный нам курс в следующий день за этими четырьмя, т.е. каждая строка таблицы с обучающей последовательностью (выборкой) представляет собой обучающий пример, где первые 4 числа — входные значения сети, а пятое число — желаемое значение выхода.

Заметим, что объем обучающей выборки зависит от выбран­ного количества входов. Если сделать 299 входов, то такая сеть потенциально могла бы строить лучший прогноз, чем сеть с 4 вхо­дами, однако в этом случае мы имеем дело с огромным массивом данных, что делает обучение и использование сети практически невозможным. При выборе числа входов следует учитывать это, выбирая разумный компромисс между глубиной предсказания (чи­сло входов) и качеством обучения (объем тренировочного набора).

Вообще говоря, в зависимости от типа решаемой задачи, це­лесообразно применять нейронную сеть наиболее подходящей для такой задачи структуры.

Эффективность нейронных сетей

Эффективность нейронных сетей устанавливается рядом так называемых теорем о полноте. Ранее в нестрогой формулировке была приведена одна из них. Рассмотрим еще одну подобную тео­рему.

В 1989 г. Funahashi показал, что бесконечно большая ней­ронная сеть с единственным скрытым слоем способна аппрокси­мировать любую непрерывную функцию, сформулировав данное утверждение в форме следующей теоремы.

Теорема. Пусть ф(х) — непостоянная, ограниченная и мо­нотонно возрастающая непрерывная функция. Пусть, далее, — ограниченное множество и

— вещественная непрерывная функция, определенная на U.

Тогда для произвольного е > 0 существует целое L и веще­ственные константы Wi, w ^ такие, что аппроксимация

удовлетворяет неравенству

Другими словами, любое непрерывное отображение может быть аппроксимировано в смысле однородной топологии на U двухслойной нейронной сетью с активационными функциями ф(х) для нейронов скрытого слоя и линейными активационными функциями для нейронов выходного слоя.

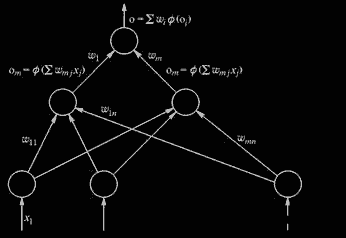
Рис. 2.21. Нейронная сеть Funahashi

На рис. 2.21 представлена НС Fu - nahashi для аппроксимации скалярной функции векторного аргумента.

Отметим еще раз, что приведенная теорема о полноте является далеко не единственной из известных.

Основными недостатками аппарата нейронных сетей являются:

• отсутствие строгой теории по выбору структуры НС;

• практическая невозможность извлечения приобретенных зна­ний из обученной НС (нейронная сеть практически всегда — «вещь в себе», черный ящик для исследователя).

Приведенный краткий материал о теории искусственных ней­ронных сетей является достаточным для перехода к следующей главе. Более подробная информация по структурам, алгоритмам обучения и использованию НС приведена, например, в рекоменду­емой литературе.