Прогноз числа авиапассажиров методами временных рядов в системе STATISTICA

Источник: http://www.statsoft.ru/statportal/tabID__71/MId__330/ModeID__0/PageID__135/DesktopDefault.aspx

В библиотеку

Постановка задачи

Ключевая задача аналитического отдела современной авиакомпании состоит в предварительной оценке и дальнейшем качественном прогнозе объема собственных перевозок и перевозок конкурентов. Заранее спланированное число авиарейсов позволяет рационально распределить ресурсы компании, не задевая при этом интересов пассажира. Подобная политика приводит к исключению неприбыльных "холостых" рейсов и к повышению рейтинга компании благодаря полному соответствию потребностям клиентов.

Организация данных

В качестве примера рассмотрим данные по количеству пассажиров за каждый месяц некоторой авиационной компании за период с января 2001 по декабрь 2003 года. Данные были представлены в таблице Excel и экспортированы в STATISTICA. Таким образом, необходимо провести анализ одной переменной с 36 наблюдениями.

Предварительный анализ

Вначале построим исходный ряд графическим методом Линейные графики. Это можно сделать с помощью контекстного меню или воспользовавшись меню Графика - 2М графики - Линейные графики.

Рисунок 1. Линейный график авиаперевозок

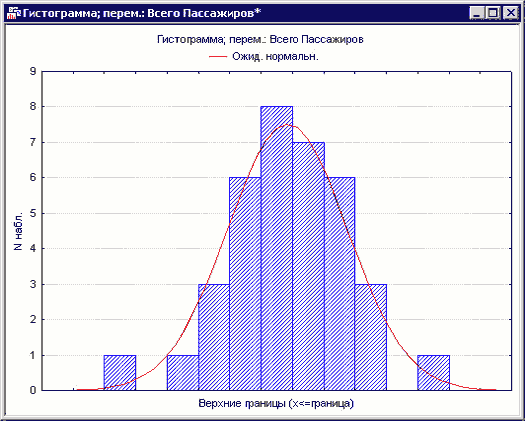
Из графика переменной отчетливо видно, что существует сезонная зависимость числа пассажиров. Построим гистограмму ряда:

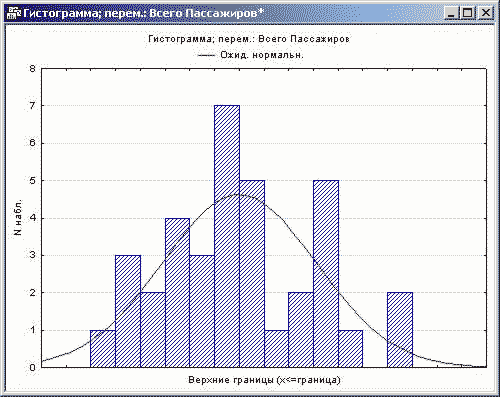
Рисунок 2. Гистограмма количества пассажиров

Гистограмма иллюстрирует тот факт, что распределение ряда не является нормальным, и в дальнейшем имеет смысл попытаться установить зависимости для этого ряда.

Анализ данных

Нахождение зависимости в представленных данных является задачей разбиения исходного ряда на 2 составляющие: детерминированную функцию и чисто случайную составляющую. Случайная составляющая должна представлять собой гауссовский ряд с независимыми приращениями.

Для установления характера неслучайной составляющей, построим Автокорреляционную функцию исходных данных:

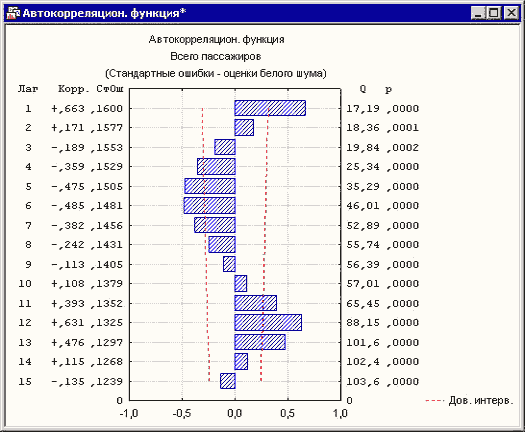
Рисунок 3. Автокорреляционная функция

По виду Автокорреляционной функции можно предположить, что ряд описывается моделью авторегрессии 2-го порядка. На графике автокорреляции достигают пиков на лагах кратных 6, и хотя, период колебаний автокорреляционной функции равен 12, что очевидно из соображений сезонности, практический расчет показывает, что более корректные результаты достигаются при  сезонном лаге равном 6.

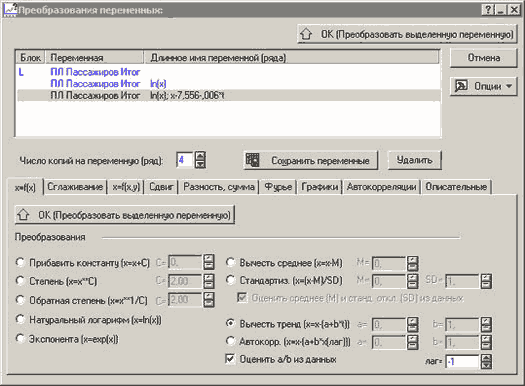
Предварительным преобразованием Логарифмирование «погасим» слабо выраженную мультипликативную природу исходного ряда, после этого вычтем тренд. Эти действия автоматизированы в системе STATISTICA, и доступны в меню Другие преобразования и графики:

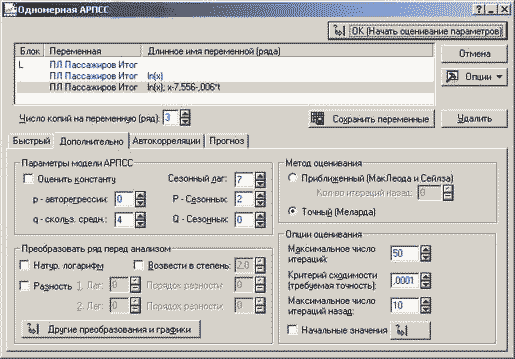
Рисунок 4. Диалоговое окно настройки преобразований переменной

Лаг первого порядка не вычитаем, т.к. в данном случае это ухудшает результат. 

Определение порядка скользящего среднего было проведено методом подбора. Наилучший результат дала модель со скользящим средним 4-го порядка.

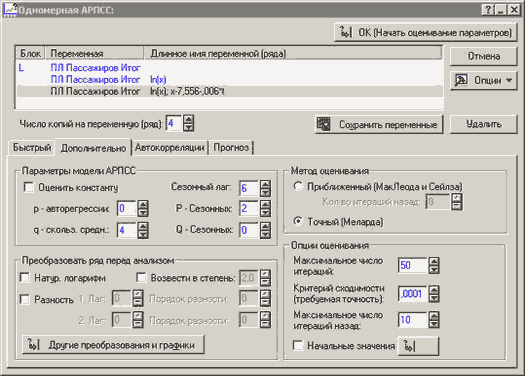
Итак, после преобразований логарифмирования и вычитания тренда зададим параметры модели:

Сезонный лаг = 6, Ps = 2, q = 4. Другие установки оставим без изменений.

Выбранная модель наиболее точно дает прогноз ряда на 8 месяцев вперед. Короткосрочный прогноз будет рассмотрен в следующих пунктах.

Произведем оценивание Точным методом:

Рисунок 5. Диалоговое окно настройки АРПСС модели

Визуальный анализ результатов

Для проверки адекватности модели воспользуемся визуальными методами, представленными в системе STATISTICA.

Как уже было сказано, случайная составляющая – остатки – должны быть нормально распределены. Для анализа остатков воспользуемся вкладкой  Подгонка распределений меню Анализ, из рисунка 6 видно, что распределение близко к нормальному. Критерии Хи-квадрат = 0,25; р = 0,88:

Рисунок 6. Гистограмма остатков в АРПСС модели

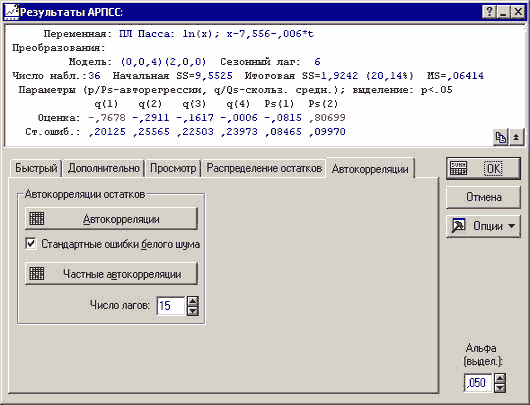
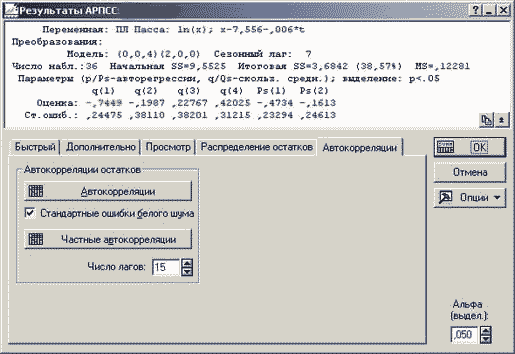
Вследствие того, что приращения случайной составляющей должны быть независимы, автокорреляции и частные автокорреляции остатков, не должны выходить за допустимые интервалы. В окне результатов АРПСС эти графики можно построить нажатием одной кнопки:

Рисунок 7. Диалоговое окно результатов АРПСС модели

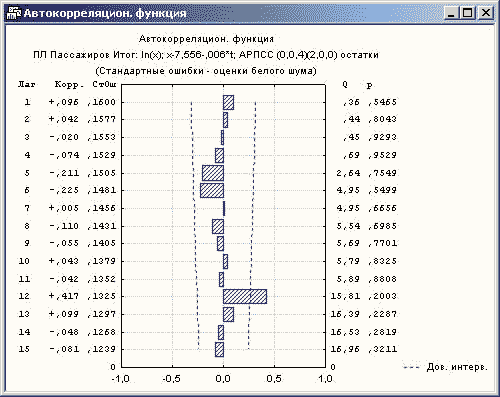
Рисунок 8. Автокорреляционная функция для остатков АРПСС модели

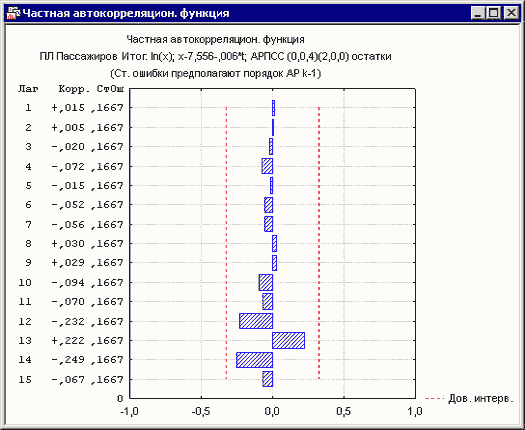
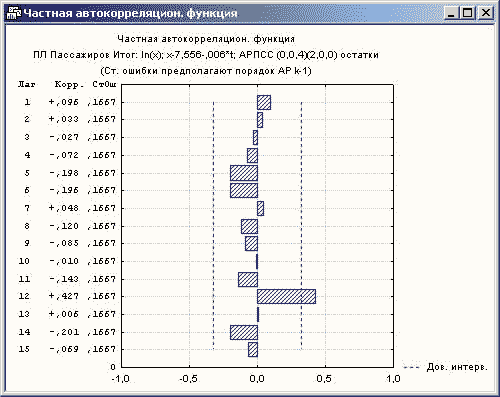
Рисунок 9. Частная автокорреляционная функция для остатков АРПСС модели

Как видно автокорреляции и частные автокорреляции (рисунок 8 и рисунок 9) целиком лежат в допустимых интервалах.

Дополнительным методом анализа адекватности модели, является график расположения остатков на нормальной вероятностной бумаге:

Рисунок 10. Диалоговое окно результатов АРПСС модели

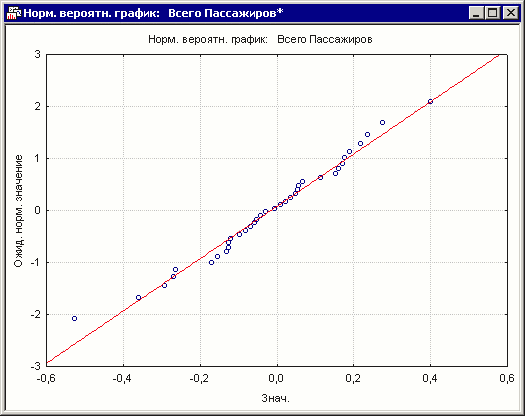
Рисунок 11. Нормальный график для остатков АРПСС модели

Точки на графике лежат близко к прямой, что хорошо характеризует модель.

Итак, модель достаточно достоверна. Посмотрим, насколько точно она предсказывает действительные наблюдения. Для этого построим прогноз по первым 80% наблюдений на оставшиеся 20%. 80% наблюдений составляют 28 месяцев, 20% - 8 месяцев.

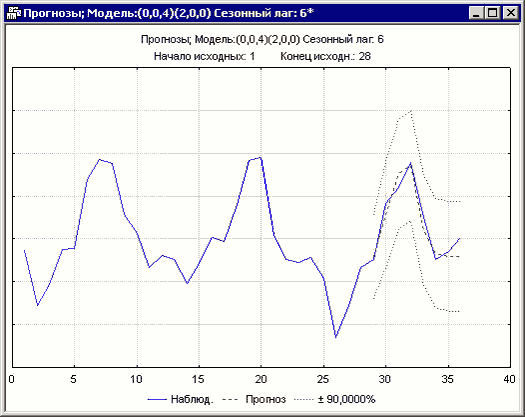
Построив график прогноза с 29 по 36 месяц, видим, что прогноз хорошо предсказывает действительные наблюдения, особенно в первые месяцы прогноза:

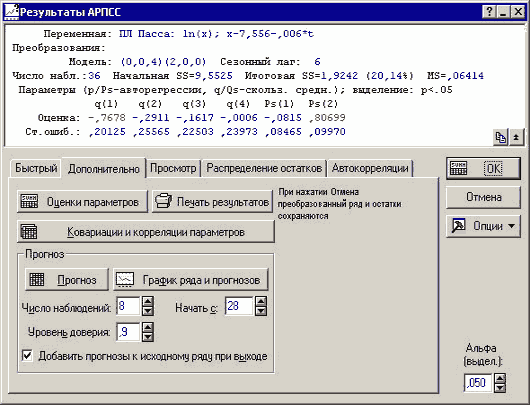
Рисунок 12. Диалоговое окно для построения прогноза

Рисунок 13. График прогноза на 8 месяцев с помощью АРПСС модели

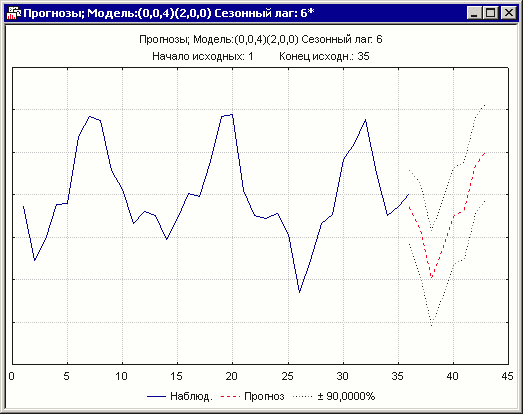
По прогнозу с 36 месяца на 20% вперед, интуитивно видно, что модель достаточно объективна:

Рисунок 14. График прогноза на 8 месяцев вперёд с помощью АРПСС модели.

Сравнение анализов с разными моделями

Попытки провести анализ с другими параметрами не дали такой высокой адекватности модели:

Анализ №2

Сезонный лаг = 6

Ps = 2   q = 3  -лаг = 1

Хи-кв = 0,71   р = 0,69

 

Анализ №3

Сезонный лаг = 12

Ps = 2  q=3  -лаг = 0

Хи-кв = 1,23   р = 0,54

 

Анализ №4

Сезонный лаг = 12

Ps = 2  q=3 -лаг = 1

Хи-кв = 4,9   р = 0,177

Видно, что вычитание первого лага сильно ухудшает адекватность модели (анализы № 2, 4). Также ее адекватность ухудшается при задании Сезонного лага = 12 (анализы № 3, 4). Были проведены многие другие анализы, которые дали плохие результаты. Во всех этих моделях точки на нормальной вероятностной бумаге хуже лежали, и наблюдались выраженные автокорреляции.

Результаты

Построим прогноз ряда по первым 80% наблюдений на оставшиеся 20%, и посмотрим насколько хорошо предсказанные данные согласуются с действительно наблюдаемыми.

Таблица 1.

Среднее значение абсолютной величины относительной ошибки равно 0,104, т.е. среднее отклонение предсказанных значений от действительных за последние 8 месяцев составляет 10,4%.

Выделение сезонной составляющей методом сезонной декомпозиции дает слишком большие нерегулярные составляющие (того же порядка, что и сезонные), поэтому данный метод в анализе не использовался.

Углубленный анализ

Прогнозирование остатков для повышения точности анализа оказалось довольно сложной задачей, т.к. остатки распределены практически равномерно и их автокорреляции близки к нулю. Выделить сезонную составляющую в ряде остатков не удалось. Построим по нашей модели прогноз ряда, начиная с 13 наблюдения, на 24 наблюдения вперед.

Рисунок 15. График прогноза на 24 месяца вперед с помощью АРПСС модели

Разность между реальными наблюдениями и предсказанными моделью после возвращения тренда и экспоненцирования будет выглядеть следующим образом:

Рисунок 16. График разностей между наблюдаемыми и прогнозируемыми значениями

Отчетливо видна некоторая периодичность, однако для проведения сезонной декомпозиции слишком мало данных.

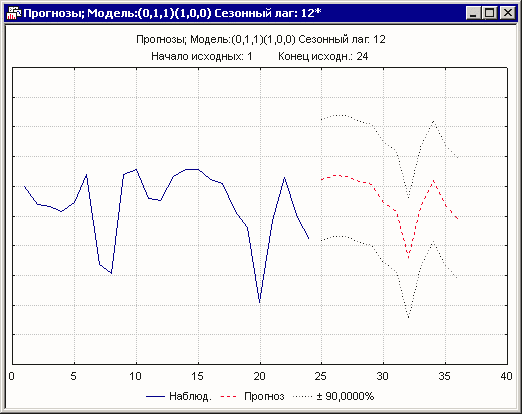
Теперь предскажем поведение этого ряда на 12 месяцев вперед (использовался точный метод АРПСС Ps=1, q=1, разность лага 1-й степени):

Рисунок 17. График прогноза на 12 месяцев вперёд методом АРПСС

Предсказанные данные будут составлять приблизительную ошибку нашего базового прогноза. Теперь для улучшения базового прогноза вычтем из него предсказанную ошибку. Вычитаем из второго столбца таблицы 1 (где находятся предсказанные данные с 29 по 36 месяц) ряд предсказанных ошибок:

Таблица 2.

Среднее значение абсолютной величины относительной ошибки в этом случае равно 0,076, т.е. среднее отклонение предсказанных значений от действительных за последние 8 месяцев составляет 7,6%.

Из рисунка 16 можно сделать вывод, что поведение ряда в каждом сезоне приблизительно одинаковое, поэтому наши операции по вычитанию ошибок имеют смысл.

Автоматизация поиска оптимальной модели

Теория математической статистики позволяет, анализируя функции корреляции и другие характеристики исходного ряда, сделать предположение о параметрах модели. С помощью средств STATISTICA Visual Basic, можно реализовать механизм автоматического перебора параметров модели, для нахождения наиболее достоверного решения. На базе STATISTICA была реализована программа, перебирающая множество моделей АРПСС, и  вычисляющая точность каждой модели, по заданному критерию.

Для ускорения времени перебора, сохраним ряд, полученный логарифмированием, и вычитанием тренда. С этим, преобразованным рядом, и будет работать программа автоматического поиска модели АРПСС. Остановимся подробно на описании программы.

Описание программы АвтоАРПСС

Назначение: Программа АвтоАРПСС предназначена для автоматизации поиска параметров модели АРПСС.

Принцип работы: Программа автоматически строит множество моделей АРПСС заданного ряда, с интервалами параметров указанными пользователем. Предоставляет пользователю таблицу, в которой указаны параметры для каждой модели, и ее ошибка. Из этой таблицы пользователь, легко может выбрать несколько наиболее точных моделей, для собственного анализа. 

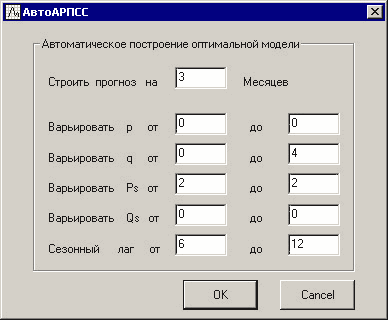
Задание значений: От пользователя требуется ввести только интервалы значений параметров модели, для которых программа автоматически построит множество прогнозов, и число проверок точности для каждой модели.

Рисунок 18. Диалоговое окно настройки параметров программы

Критерий точности: нас интересует краткосрочный прогноз, ошибка определяется следующим образом: программа строит n (указанное пользователем) прогнозов на 1 наблюдение, начиная с какого-то l-n-го и заканчивая l-тым наблюдением (где l длина ряда). Для каждого прогноза берется разность между предсказанным значением и наблюдаемым в действительности (остаток). Затем вычисляется среднее арифметическое модуля остатка.

Так, например, задав для параметров модели интервалы: p=0, q= от 0 до 4, Ps = 2, Qs=0, cезонный лаг = от 6 до 12, и число проверок n=3. Мы получим следующую таблицу:

Рисунок 19. Таблица данных, полученная по результатам работы программы

В ней в первый 5-ти столбцах записаны параметры модели.
В 6-м столбце стандартное отклонение,
в 7-м столбце  находится среднее значение абсолютной величины ошибки по всем 3-м месяцам,
в 8-м, 9-м и 10-м столбцах произведены прогнозные значения на три месяца (эти данные не приводятся из-за большого размера таблицы).
Таблицу можно отсортировать по возрастанию 7-го столбца.

Программа работала около трех минут. Задав вариацию параметров в более широких пределах, а также вариацию всех переменных, можно достичь более точного результата. После сортировки были получены следующие результаты: наилучший результат дала модель со скользящим средним 4го порядка, сезонной авторегрессии 2-го порядка и сезонным лагом равным 7.

Замечание: Для автоматического поиска параметров модели долгосрочного прогнозирования можно воспользоваться аналогичной программой AutoArimaLG.

Анализ данных

Получив результаты с помощью программы автоматического построения оптимальной модели, можно построить собственный прогноз для более полного анализа и проверки модели на адекватность.

Итак, после преобразований логарифмирование и вычитание тренда зададим параметры АРПСС модели:

Сезонный лаг = 7  Ps = 2   q = 4. Другие установки оставим без изменений.

Произведем оценивание Точным методом.

 Рисунок 20. Диалоговое окно настройки АРПСС модели

Визуальный анализ результатов

Для проверки адекватности модели воспользуемся визуальными методами, представленными в системе STATISTICA.

Анализируя остатки анализом Подгонка Распределений (рис. 21), что распределение близко к нормальному.
Критерии Хи-квадрат = 0,33; р = 0,56:

Рисунок 21. Гистограмма остатков в АРПСС модели

Построим графики автокорреляции и частные автокорреляции остатков:

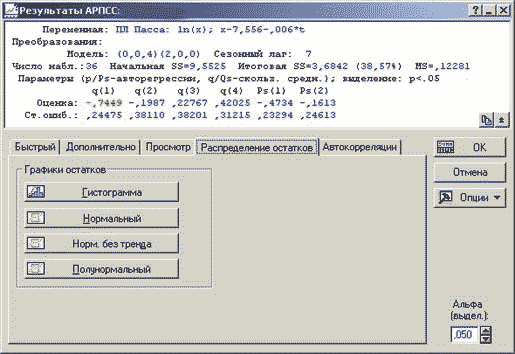
Рисунок 22. Диалоговое окно результатов АРПСС модели

Рисунок 23. Автокорреляционная функция для построенной модели

Рисунок 24. Частная автокорреляционная функция для построенной модели

Видно, что автокорреляции и частные автокорреляции (рис. 23,24 ) выходят за допустимые пределы на 12-м лаге. Эти выходы не наблюдались бы в том случае, если бы мы строили более-менее долгосрочный прогноз. Сейчас нашей целью является построение прогноза на 1 месяц, и критерием точности модели является соответствие предсказания на 1 месяц вперед.

Построим график остатков на вероятностной бумаге:

Рисунок 25. Диалоговое окно результатов АРПСС модели

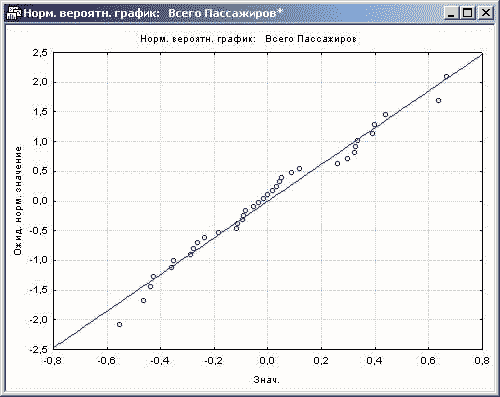
Рисунок 26. Нормальный график для построенной модели

Точки на графике лежат близко к прямой, что хорошо характеризует модель.

Посмотрим, насколько точно модель предсказывает  действительные наблюдения. Для этого построим прогноз по первым 33 наблюдениям на оставшиеся 3:

Рисунок 27. Диалоговое окно для построения прогноза

 Построив график прогноза с 34 по 36 месяц, видим, что прогноз хорошо предсказывает действительные наблюдения, особенно в первые месяцы прогноза:

Рисунок 28. График исходного ряда и прогноза на 3 месяца с помощью АРПСС модели

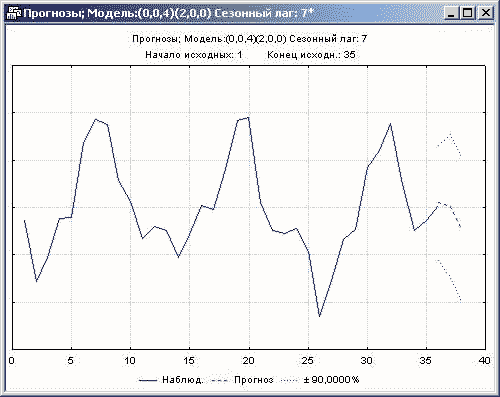
По прогнозу с 36 месяца на 3 месяца вперед, интуитивно видно, что модель достаточно объективно ведет себя и в будущем:

Рисунок 29. График исходного ряда и прогноза на 3 месяца вперёд с помощью АРПСС модели

Если полученной предсказанной величине «вернуть» тренд и взять от нее экспоненту, то получим предсказанное число пассажиров на 34-й - 36-й месяцы (второй столбец). Сравнив это число с действительным числом пассажиров (первый столбец), находим, что среднее модуля относительной ошибки по 3 месяцам равно 0,054, т.е. 5,4%:

Таблица 3.

Это предсказания не на 3 месяца вперед, как можно подумать, а 3 предсказания на 1 месяц, каждое из которых начиналось в разные месяцы. Таким образом, и ошибка является средней ошибкой предсказания на 1 месяц вперед за 3 раза.

Вывод

Как было показано, в системе STATISTICA легко реализуются различные виды анализов, на разные периоды времени, с разной точностью.

Кроме того, на графиках прогнозов представлено наиболее вероятное поведение ряда – красным цветом, и допустимые интервалы, в которых ряд будет лежать с вероятностью 90% - зеленым цветом. Также эти данные представлены в таблицах прогнозов. Это позволяет сделать выводы, не только об ожидаемом числе пассажиров, но и о максимально и минимально возможном. Исходя из этих данных, авиакомпания может распланировать авиарейсы в соответствии со своей политикой.

Методы STATISTICA Visual Basic позволяют автоматически найти нужный прогноз с нужной степенью точности простым методом перебора, не зная заранее природу модели! Это позволяет строить прогнозы "с нуля" - без каких либо подготовительных анализов и не обладая обширными знаниями в теории математической статистики.