Вопросы оптимизации объемов пассажирских перевозок транспортных компаний

В.Г.Дубинина

Источник: http://www.cognitive.ru/innovation/sbornic6/index.htm

В библиотеку

Рассмотрим авиакомпанию, работающую на конкретном рынке, как динамическую систему, рис.1. В общем случае входными переменными такой системы являются цена (тарифы, ср. стоимость билета) и качество продукта – перевозки. Выходной координатой системы является спрос на этот продукт. Как видно из рис.1, управляющими параметрами системы перевозчик-рынок являются тарифы и объёмы перевозок. Именно значения этих параметров авиакомпания может достаточно точно контролировать.

Для формализации постановки задачи воспользуемся методом гарантиро ванного статистического оценивания параметров процессов и систем[1].

 

 Рис.1

В соответствии с этим методом самый наихудший, нежелательный вид функции спроса, минимизирующий риск получения ошибочных оценок, имеет вид:

,

где

С – цена; V – объём перевозок в пассажирокилометрах ( RPK );

a, b - коэффициенты экспоненты.

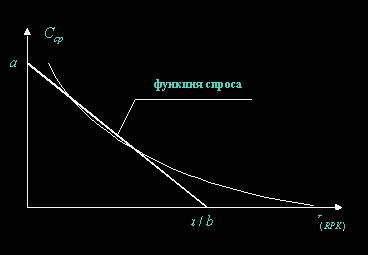
На практике применяется аппроксимация исходной экспоненициальной функции и приведение её к линейному виду (классический вид функции спроса):

(цент/ RPK ).

По смыслу коэффициент а означает платежеспособность рынка (максимальная цена, которую может ещё пассажир заплатить); отношение a / b – имеет смысл емкости (вместимости) рынка, см. рис.2.

Зная функцию спроса, всегда можно определить доходы от продажи перевозок, т.е. выручку:

Далее представим операционные затраты на выполнение авиаперевозки в виде:

Рис. 2.

,

где р – затраты, не зависящие от полета;

q - затраты, зависящие от полета.

Тогда величина прибыли авиакомпании M от выполненной авиаперевозки будет равна:

.

 График функции прибыли, рис.3, имеет экстремум, определяемый значениями:

и

.

M($)
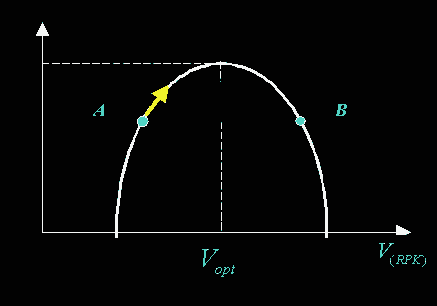
Рис. 3.

В зависимости от того, в какой точке находится система, стратегия изменения объёма перевозок будет разной. Иначе говоря, правила принятия решений:

для т. A : dM / dV > O RPK следует увеличивать.

для т. B : dM / dV < O RPK следует уменьшать.

Эластичность (вариабельность) прибыли по объёму перевозок RPK будет равна:

,

где

- доля (удельный вес) независящих от полета расходов;

- рентабельность авиаперевозки (рейса).

Если 70% и =20%, то изменение (+/-) объёмов перевозок ( RPK ) на 1%

приведет к изменению прибыли на 4,5%, т.е. существенно как т. А или В близко расположена к ординате со значением .

Эластичность (вариабельность) по тарифу (ср. стоимости билета) будет:

Тогда если =20%, то изменение тарифа на 1% приведет к изменению прибыли на 6%.

Данный метод оптимизации загрузки с учетом эластичности рынка дает хорошие по точности результаты в задачах краткосрочных (оперативных) прогнозов авиаперевозок.

Определим оптимальный пассажирооборот на линии Москва-Лондон.

Статистика перевозок за 2003 год приведена в Таблице 1.

Таблица 1

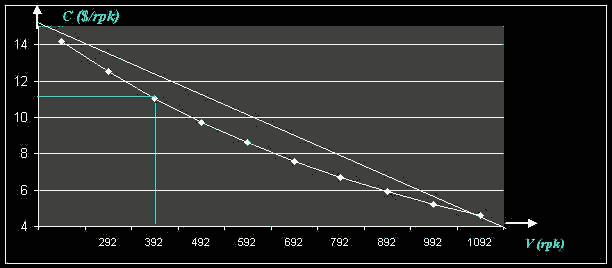
Строим зависимость доходной ставки от пассажирооборота (рис.4):

,

соответствующие коэффициенты приведены в Таблице 2

Таблица 2

Рис.4

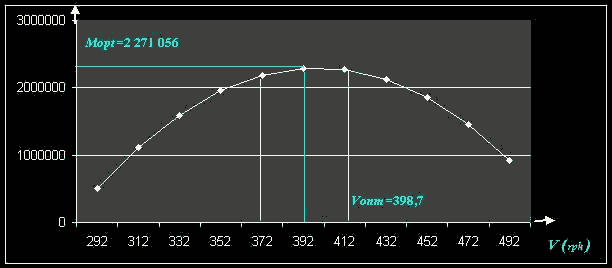
Зависимость прибыли от пассажирооброта подчиняется следующему закону (Рис.5)

Рис.5

Отсюда определяются

Исходя из полученных зависимостей находим оптимальные частоты, при которых прибыль будет максимальной. Полученные результаты приведены в Таблице 3.

Таблица 3

 

Литература:

1. Алексахин С.В. «Прикладной статистический анализ». «Приор», Москва-2001.