Трудно найти другую сферу инженерной деятельности, успехи в которой за полувековой период были бы сравнимы с достижениями в области вычислительной техники. Это, прежде всего, фантастические результаты в области роста быстродействия компьютеров, объемов оперативной и внешней памяти, микроминиатюризации, сетевых технологий, распределенных баз данных, машинной графики и мультимедийных систем.
Тем не менее, достижения в области компьютерного зрения и слуха являются несоизмеримыми и представляются куда более скромными. Этот дисбаланс становится все более нетерпимым в условиях возрастания потребностей в создании интеллектуальных систем, снабженных зрением и слухом и приближающихся по возможностям к человеку. В развитых странах наметился значительный рост публикаций и финансирования в направлении ликвидации этого противоречия [1].
Все большее распространение получили системы автоматизированного ввода информации через различные типы сканеров (ручные, листовые, барабанные, графические планшеты, дигитайзеры, факс-модемы), а также цифровые фото- и видеокамеры. При этом по разрешающей способности такие системы ввода вполне приближаются к зрению человека или животных, а с учетом быстродействия ближайшей технической моделью глаза, очевидно, являются видео- и цифровые фотокамеры. Так ПЗС матрица цифровой фотокамеры обеспечивает разрешение до 3 млн. пикселей на кадр, а современным высокопроизводительным компьютерам вполне доступна несложная обработка в реальном масштабе времени, например, пространственная плоско - параллельная корреляция.
Тем не менее, возможности интеллектуального анализа изображений с помощью компьютеров оставляют желать большего. Необходимость углубленной их обработки и распознавания требуют, по крайней мере, две области технических приложений; робототехника и экспертные системы. Промышленные роботы, снабженные компьютерным зрением позволяют сравнительно быстро к дешево производить переналадку производства на выпуск новой продукции, а транспортные роботы благодаря зрению обеспечивают надежную ориентацию в пространстве. Экспертные системы, опирающиеся на базы данных, включающие изображения, для поиска и распознавания заданных объектов требуют быстрого и надежного анализа оцифрованной видеоинформации в специализированных архивах изображений либо в базах Интернет.
Какие возможности предлагают современные стандартные программные средства в этой области? Наиболее распространенные пакеты растровой и векторной графики (Adobe Illustrator, PhotoShop, CorelDraw, CorelPhotoPaint, 3D Studio Max, Maya и др.) обладают мощными средствами создания изображений, в том числе объемных и динамических, однако, обработка ограничивается фактически подавлением случайных помех и муаров с помощью ограниченного набора фильтров (типа сглаживающих и медианных). Значительного прогресса достигла обработка документов со сканера. Последняя версия FineReader 5.0 уже позволяет производить автоматическую сегментацию страниц документа, т.е. выделение блоков текста, таблиц, картинок и графиков, подрисуночных подписей. Повышена также надежность распознавания текста за счет применения усовершенствованного алгоритма, основанного на структурно-дифференциальном контурном подходе. Благодаря этому появилась возможность понимать тексты на 176 языках народов мира и основных языках программирования.
Таким образом, успехи по распознаванию букв и цифр в документах и текстах впечатляют, также как и другие значительные достижения по анализу изображений специального вида ( например, распознавание треков ядерных частиц, идентификация автомобилей-нарушителей по фотоснимкам, анализ и распознавание сигналов в медицине и геологии). Однако, универсальных методов обработки изображений, сравнимых по эффективности с интеллектуальными возможностями человека, еще не найдено, что стимулирует активную деятельность ученых в этом направлении [1,2].
Обработка изображений с целью их распознавания является одной из центральных и практически важных задач при создании систем искусственного интеллекта.
Проблема носит явно выраженный комплексный иерархический характер и включает ряд основных этапов: восприятие поля зрения, сегментация, нормализация выделенных объектов, распознавание. Такой важный обязательный этап как понимание (интерпретация) изображений включается частично в этап сегментации и окончательно решается на этапе распознавания. Основным элементом любой задачи распознавания изображений является ответ на вопрос: относятся ли данные (входные) изображения к классу изображений, который представляет данный эталон? Казалось бы, ответ можно получить, сравнивая непосредственно изображение с эталонами (или их признаки). Однако возникает ряд трудностей и проблем, специфических, в особенности, при создании систем технического зрения (СТЗ):
1. Изображения предъявляются на сложном фоне.
2. Изображения эталона и входные изображения отличаются положением в поле зрения.
3. Входные изображения не совпадают с эталонами за счет случайных помех.
4. Отличия входных и эталонных изображений возникает за счет изменения освещенности, подсветки, локальных помех.
5. Эталоны и изображения могут отличать геометрические преобразования, включая такие сложные как аффинные и проективные.
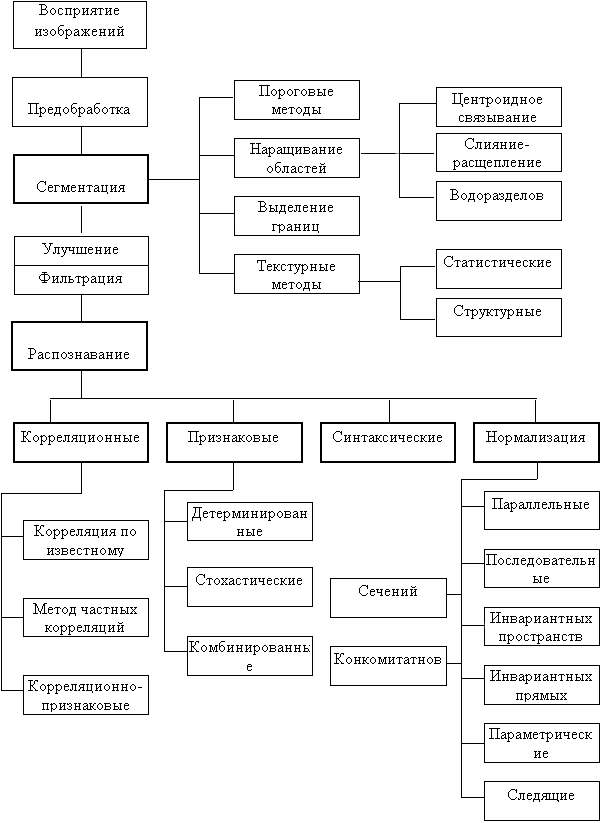
Для решения задачи в целом и на отдельных ее этапах применяются различные методы сегментации, нормализации и распознавания. Литературные источники, например [1,2,3], и многолетний опыт работы в области обработки зрительных картин позволяет предложить классификацию основных методов обработки и распознавания СТЗ изображений в соответствии со схемой, приведенной на рис.1. На схеме указаны основные процедуры и методы обработки от начального этапа восприятия поля зрения посредством датчиков, например, телекамеры до конечного, которым является распознавание.
Рисунок 1 – Основные процедуры и методы распознавания изображений
Операция предобработки применяется практически всегда после снятия информации с видеодатчика и преследует цель снижения помех на изображении, возникших в результате дискретизации и квантования, а также подавления внешних шумов. Как правило, это операции усреднения и выравнивания гистограмм.
Сегментация
Сегментация обычно понимается как процесс поиска однородных областей на изображении. Этот этап весьма трудный и в общем виде не алгоритмизированный до конца для произвольных изображений. Наиболее распространены методы сегментации, основанные на определении однородных яркостей (цветов) или однородностей типа текстур.
При существовании стабильных различий в яркостях отдельных областей поля зрения применяются пороговые методы. Метолы наращивания областей эффективны при наличии устойчивой связности внутри отдельных сегментов. Метод выделения границ хорошо применять, если границы достаточно четкие и стабильные. Перечисленные методы служат для выделения сегментов по критерию однородных яркостей. Заметим, что один из самых эффективных методов наращивания областей предполагает выбор стартовых точек либо с помощью оператора (алгоритм центроидного связывания), либо автоматически. Эффективным здесь представляется метод водоразделов, основанный на поиске локальных минимумов с последующей группировкой вокруг них областей по связности. Все методы весьма приемлемы с точки зрения вычислительных затрат, однако, для каждого из них характерна неоднозначность разметки точек в реальных ситуациях из-за необходимости применения эвристик (выбор порогов совпадения яркостей, выбор цифровых масок и т.д.). Заслуживает внимания в связи с этим предложенный метод многозначной разметки, основанный на комбинации различных приемов для снижения неопределенности. Важное практическое значение имеют допускающие параллельную обработку алгоритмы ускорения процесса разметки на основе логического анализа соседних элементов [3].
Для описания и сегментации свойств изображений, именно, однородности, шероховатости, регулярности, применяют текстурные методы делящиеся условно на две категории: статистические и структурные. Примером статистического подхода является использование матриц совпадений, формируемых из исходных изображений, с последующим подсчетом статистических моментов и энтропии. При структурном подходе, например, на основе мозаики Вороного, строится множество многоугольников. Многоугольники с общими свойствами объединяют в области. Для исследования общих свойств часто используют признаки - моменты многоугольников.
После сегментации возникают помехи в виде как разрозненных изменений изолированных элементов изображения, так и в виде искажений некоторых связных областей. Не останавливаясь подробно на методах борьбы с подобными помехами, отметим лишь, что на практике наибольшее распространение получили цифровые фильтры-маски и нелинейные фильтры типа медианных. При этом в случае сегментации путем выделения границ использование усредняющих фильтров-масок невозможно, так как границы при этом не подчеркиваются, а размываются. Для подчеркивания контуров применяются специальные операторы интегрального типа.
Распознавание
Распознавание - чаще всего конечный этап обработки, лежащий в основе процессов интерпретации и понимания. Входными для распознавания являются изображения, выделенные в результате сегментации и, частично, отреставрированные. Они отличаются от эталонных геометрическими и яркостными искажениями, а также сохранившимися шумами.
Для реальных задач распознавания применяются, в основном, четыре подхода, использующие методы: корреляционные, основанные на принятии решений по критерию близости с эталонами; признаковые и синтаксические - наименее трудоемкие и нормализации, занимающие промежуточное положение по объему вычислений.
Каждый из подходов в распознавании имеет право на существование. Более того, в рамках каждого подхода есть свои конкретные алгоритмы, имеющие определенную область применения, которая зависит от характера различий входных и эталонных изображений, от помеховой обстановки в поле зрения, требований к объемам вычислений и скорости принятия решений.
Корреляционные методы нашли широкое применение при обнаружении и распознавании изображений в системах навигации, слежения, промышленных роботах. При полностью заданном эталоне многошаговая корреляция путем сканирования входного поля зрения является по сути полным перебором в пространстве сигналов. Поэтому эту процедуру можно считать базовой, потенциально наиболее помехоустойчивой, хотя и самой трудоемкой. Все остальные методы направлены на сокращение вычислительных затрат при попытке обеспечения наперед заданной надежности распознавания, габаритно-весовых характеристик вычислителя и стоимости расходов на создание программных и технических средств. Однако, сколь-нибудь строгой математической модели оптимизации подобной задачи еще не создано.
Значительно более простые с точки зрения вычислительной сложности методы основаны на переходе в пространство признаков, которые характеризуются существенно меньшей размерностью по сравнению с пространством сигналов (изображений). В зависимости от поставленной цели (например, достижения заданной точности) выполняется корреляционная обработка признаков, полученных от эталона и входного изображения как с использованием порогов по величине сходства, так и без установления порога (когда ищется максимум сходства). При этом актуальной является задача комплексирования разнотипных и разно шкальных признаков (метрических, статистических, логических, текстурных, структурно-лингвистических и др.), полученных различными измерительными средствами с целью решения задачи распознавания (обнаружения). Новые подходы, основанные на параллельно-фрагментной обработке комплексированных данных корреляционным методом, изложены в [4].
Наиболее помехоустойчивы при действии как случайных помех, так и локальных помех являются алгоритмы, основанные на методе частных корреляций. При этом частные коэффициенты корреляций, полученные для отдельных фрагментов эталона в сигнальном пространстве могут рассматриваться как признаки (в общем случае разно шкальные). Обработка таких признаков, т.е. их свертка, зависит от типа изображений, помеховой обстановки (например, степени заслонения полезного изображения, наличия ложных изображений в поле зрения) и может быть осуществлена методами проверки статистических гипотез [3,4].
Признаковые и синтаксические методы - наиболее разработаны в теории распознавания образов. Они основаны как на статистических, так и детерминированных подходах. Главную трудность в признаковых методах составляет выбор признаков. При этом исходят из естественных правил: а)признаки изображений одного класса могут различаться лишь незначительно (за счет влияния помех); б)признаки изображений разных классов должны существенно различаться; в)набор признаков должен быть минимально возможным, т.к. от их количества зависит и надежность, и сложность обработки.
В первом приближении синтаксические методы можно отнести к признаковым, т.к. они основаны на получении структурно-лингвистических признаков, когда изображение дробится на части - непроизводные элементы (признаки). Вводятся правила соединения этих элементов, одинаковые для эталона и входного изображения. Анализ полученной таким образом грамматики обеспечивает принятие решений.
Алгоритмы корреляционно-признаковых и признаковых методов достаточно близки и первые можно рассматривать как частный случай вторых. Хотя признаковые методы и не обладают такой помехозащищенностью как чисто корреляционные или методы частных корреляций (в сигнальных пространствах), однако, благодаря меньшим трудозатратам, их применение полезно на первом этапе, когда решается задача о неэквивалентности. При этом часть входных изображений, признаки которых не соответствуют ни одному из эталонов, отбрасываются сразу.
Нормализация
Методы нормализации при распознавании занимают промежуточное место между сигнальными корреляционными и признаковыми алгоритмами. В отличие от признаковых при нормализации изображение не “теряется”, а только замещается изображением того же класса эквивалентности. В то же время, в отличие от корреляционных методов, множество входных изображений заменяется множеством нормализованных изображений. Каждое нормализованное изображение, в общем случае, находится гораздо ближе к своему эталону (с позиции групповых преобразований), что значительно сокращает количество корреляций на завершающем этапе распознавания. Суть нормализации заключается в автоматическом вычислении неизвестных параметров преобразований, которым подвергнуты входные изображения, и последующем приведении их к эталонному виду. Процедура преобразований производится с помощью операторов нормализации (нормализаторов), а вычисление параметров выполняется функционалами, действующими на множестве изображений. В монографии [3] подробно излагаются параллельные и последовательные, параметрические и следящие нормализаторы, которые нашли эффективное применение для базовых преобразований: смещений, поворотов, растяжений, косых сдвигов и некоторых их комбинаций. Остается открытым вопрос о поиске универсальных и надежных нормализаторов для сложных групп преобразований – аффинных и проективных.
Параллельная нормализация методом сечений не всегда приводит к однозначному определению параметров аффинных или проективных преобразований, несмотря на кажущуюся универсальность. В самом деле, всякий раз для нового изображения возникает вопрос о рациональном разбиении на градации яркости полутоновых изображений. Это требует постоянного присутствия оператора и интерактивного режима работы. Кроме того изображения типа “силуэт”, а также малоградационные вообще не поддаются нормализации этим методом.
Метод полиномиальных конкомитантов обладает значительной общностью и универсальностью, однако имеет чрезвычайно высокую вычислительную трудоемкость и невысокую точность в связи с накоплением ошибок вычислений.
Наибольший интерес на данном этапе развития теории нормализации представляют последовательные методы, основанные на поэтапном вычислении параметров сложных преобразований и применении частичных нормализаторов на каждом этапе. Последовательные методы предполагают возможность разложения сложных групп на более простые подгруппы. Например, аффинную группу преобразований Gа можно представить в виде суперпозиции центроаффинной Gр и группы параллельных смещений: Gа=GpGc. Это разложение позволяет ставить вопрос о последовательной нормализации с помощью суперпозиции частичных: Fа= FpFc, где Fc- нормализатор центрирования (смещений), а Fр- нормализатор центроаффинной группы, которая однозначно определяется матрицей А=(аij), i,j=1,2…
В свою очередь, чтобы применить частичные нормализаторы к центроаффинным преобразованиям изображений, необходимо уметь разлагать матрицу А на составляющие. При этом не все разложения равноценны с точки зрения практической реализации.
Так общеизвестно представление квадратной матрицы в виде комбинации самосопряженной и ортогональной. В свою очередь самосопряженную матрицу можно выразить произведением ортогональной из собственных векторов, диагональной и обратной ортогональной. В результате А=K/\L, где K, L-ортогональные матрицы, в частности, повороты, /\ -вещественная диагональная матрица.
Это разложение, в принципе, можно использовать для построения суперпозиции соответствующих частичных нормализаторов аффинной группы [3]. Однако, практическое применение указанного разложения вызывает большие трудности. В частности, возникает неоднозначность при равенстве масштабных коэффициентов матрицы /\ (теряет смысл второй поворот). Кроме того, возникают существенные ограничения на величины углов поворотов, которые можно определить (не более p/4).
Другие разложения, полученные нами в последнее время, именно А=/\XU, A=Y/\X, A=/\YU, A=/\YX, где X,Y- соответственно матрицы косых сдвигов вдоль оси x и вдоль оси y, U-матрица поворота, оказываются практически более удобными и не имеют ограничений, отмеченных выше. В этой связи значительный интерес представляет разрабатываемый в настоящее время подход, основанный на инвариантных прямых при аффинных преобразованиях. Речь идет о фундаментальном свойстве аффинной группы преобразований: прямые переходят в прямые независимо от конкретных параметров преобразований. Доказана возможность перехода от двумерного анализа изображения к анализу его линейных сечений, что позволяет не только упростить вычисления, но и достичь прогресса в расширении типов допустимых входных изображений. Этому в решающей степени способствуют новые разложения центроаффинной группы, приведенные выше.
Определенный интерес представляет применение инвариантных процедур по полю зрения [4]. Так применение преобразований по модулю Фурье позволяет произвести автоматическое центрирование изображений. Модуль преобразования Меллина инвариантен к изменению масштабов по осям. На базе оператора Гаммерштейна строятся инварианты к центроаффинным преобразованиям. Такие операторы позволяют применять последовательную нормализацию при сложных преобразованиях вплоть до проективных. Однако, эксперименты показывают, что их эффективное использование возможно только для хорошо сегментированных изображений. При этом объемы вычислений в реальных системах часто выходят за рамки допустимых.
Нормализация проективных преобразований представляет собой трудную и еще не решенную до конца задачу. Прогресс достигнут по отдельным подгруппам проективной группы, которая характеризуется в общем 8 независимыми параметрами. Так для нормализации ортогональной проективной подгруппы, которая характеризуется 3 параметрами, получены функционалы общего вида:
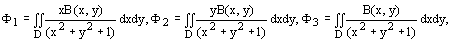
где B(x,y)-функция яркости изображения, D-поле зрения.
Для простейших проективных преобразований типа перспективы
,
получены подходящие нелинейные функционалы типа отношения моментов. Однако, ядра моментов содержат отрицательные степени координат x, y, что ограничивает область анализа изображений полуплоскостями или даже отдельными квадрантами. Учитывая ограниченные возможности методов сечений и конкомитантов, универсальные и практически пригодные методы нормализации проективных преобразований следует искать на пути применения частичных операторов. Можно показать, что любое проективное преобразование можно разложить на аффинные и простейшие проективные, например,
или преобразование перспективы. Это дает принципиальную возможность применить суперпозицию частичных нормализаторов. Однако, условия синтеза нормализаторов требуют поиска таких, которые обладают свойствами перестановочности и устойчивости [3]. Дополнительные вопросы вносят многочисленные условия и ограничения на коэффициенты проективных преобразований, возникающие в реальных условиях.
Однако, несмотря на приведенные трудности, нет принципиальных ограничений на построение нормализаторов проективных преобразований, которые лежат в основе монокулярного восприятия окружающего мира органом зрения человека и задача эта будет в конце концов решена. Это будет этапным моментом в решении проблемы распознавания изображений.
Заключение
Процесс распознавания изображений является сложной многоэтапной процедурой. Многоэтапность (иерархичность) обусловлена тем, что различные задачи обработки на самом деле тесно связаны и качество решения одной из них влияет на выбор метода решения остальных. Так выбор метода распознавания зависит от конкретных условий предъявления входных изображений, в том числе характера фона, других изображений, помеховой обстановки и связан с выбором методов предобработки, сегментации, фильтрации.
Однако, для типичных ситуаций, на основе проведенного в статье анализа, можно предложить универсальную иерархическую структуру распознавания. На первом этапе применяются наименее трудоемкие признаковые алгоритмы для решения задачи о неэквивалентности входных изображений и эталонов. Входное множество изображений при этом существенно сокращается. На втором этапе оставшиеся изображения подвергаются нормализации. На третьем - нормализованные изображения классифицируются одним из конструктивных способов, например корреляционным. При такой структуре распознавания время решения задач сокращается в сотни раз.
1. Handbook of pattern recognition and computer vision / Chen C.H., Rau L.F. and Wang P.S.P.(eds.). – Singapore-New Jersey-London-Hong Kong: World Scientific Publishing Co. Pte. Ltd., 1995. - 984 p.
2. Shalkoff R.J. Digital image processing and computer vision. – New York-Chichester-Brisbane-Toronto-Singapore: John Wiley & Sons, Inc., 1989. - 489 p.
3. Путятин Е.П., Аверин С.И. Обработка изображений в робототехнике. М: Машиностроение, 1990. 320 с.
4. Гиренко А.В., Ляшенко В.В., Машталир В.П., Путятин Е.П. Методы корреляционного обнаружения объектов. Харьков: АО “БизнесИнформ”, 1996. 112 с.
5. Вестник Национального Технического Университета “Харьковский политехнический институт” Выпуск 114.- Харьков: НТУ “ХПИ”, 2001. – 128с. 7. Прблемы бионики. Всеукраинский межведомственный сборник. Выпуск 50.- Харьков: “ХГТУРЭ”, 1999. – 217с.