Повитухин С. А. Математическая модель охлаждения
слитка в кристаллизаторе при разлике под шлаком
Адрес источника: http://www.ict.nsc.ru/ws/YM2005/9345/index.html
Из всех
технологий, применяемых в настоящее время в промышленности при производстве
стали, только способ непрерывной разливки может быть назван
перспективным. Главным достоинством машин непрерывного литья заготовок (МНЛЗ),
по сравнению с разливкой стали в изложницы, является высокий выход годного
металла. Несмотря на значительные успехи, достигнутые в нашей
стране и за рубежом в области использования непрерывного литья стали,
перед металлургами стоят новые задачи в области совершенствования технологии,
улучшения качества литого и катаного металла, расширения сортамента профилей и
марок стали и сплавов, разливаемых на МНЛЗ. Для решения этих сложных и
трудоемких задач большое значение имеют фундаментальные теоретические и
экспериментальные исследования.
Долгие годы внедрение непрерывной
разливки стали, широкого размерного и марочного сортамента, сдерживалось из-за
низкого качества поверхности непрерывнолитых заготовок. Применение
шлакообразующих смесей (ШОС) для создания защитной среды в кристаллизаторе и
промежуточных ковшах кардинально улучшило качество заготовок широкого
сортамента и способствовало резкому увеличению их производства. При разливке
металла под шлаком смазку и изоляцию оболочки слитка в кристаллизаторе
осуществляет гарнисаж, т. е. шлак, расположенный ниже
зеркала металла между оболочкой слитка и стенками кристаллизатора. Гарнисаж значительно влияет на тепловые потоки от оболочки
слитка к стенкам кристаллизатора. Однозначного решения вопроса о степени
влияния различных факторов на качество макроструктуры слитков по отдельным
видам дефектов в литературных источниках нет. Обусловлено это тем, что каждая
из МНЛЗ представляет собой сложный агрегат со своей спецификой как в технологии
разливки металла и конструкции зоны вторичного охлаждения, так и в
обслуживании.
Решение проблемы оптимизации
технологических процессов в настоящее время не может ограничиться чисто
эмпирическими подходами, основанными на обобщении производственного опыта, так
как экспериментальное измерение температур в непрерывнолитом
слитке является трудоемкой технической задачей. В связи с этим
совершенствование технологии непрерывной разливки идет в направлении создания
математических моделей, описывающих технологические процессы с учетом большого
числа технологических и конструктивных факторов.
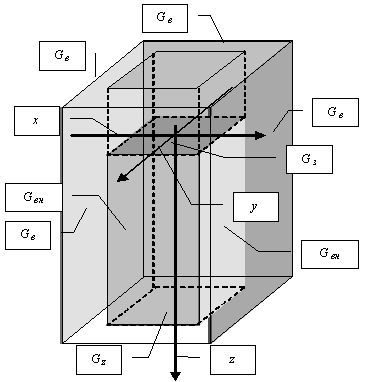 Математическая модель работы кристаллизатора МНЛЗ,
принципиальная схема которого приведена на рисунке, должна учитывать локальные
влияния гарнисажа на формирование теплового потока и факторы,
определяющие это влияние. Существующие в настоящее время модели этого не
делают. Влияние гарнисажа на процесс кристаллизации
металла устраняется либо заданием коэффициентов теплопередачи по высоте, либо
заданием теплового потока на границе металла и шлака. В обоих случаях в решение
задачи вводятся заведомо неизвестные характеристики, что приводит к
необъективности математической модели. Причем, при стремлении упростить решение
задачи моделирования процессов кристаллизации слитка, многие исследователи
рассматривают плоскопараллельные, стационарные модели, которые в принципе не
могут хорошо описать изучаемые явления. Следует отметить, что все известные в
литературе модели и алгоритмы контроля и управления тепловыми процессами в
кристаллизаторе МНЛЗ получены путем вышеуказанных упрощений, и, следовательно,
имеют ограниченную область применения. В связи с этим исследование, связанное с
построением модели охлаждения слитка в кристаллизаторе, с учетом влияния
шлаковой прослойки представляется актуальным.
Кроме того, разработка методики решения нестационарной, пространственной задачи Стефана представляет большой научный
интерес, так как расширяет возможности решения очень сложных краевых задач,
связанных с фазовыми переходами.
Математическая модель работы кристаллизатора МНЛЗ,
принципиальная схема которого приведена на рисунке, должна учитывать локальные
влияния гарнисажа на формирование теплового потока и факторы,
определяющие это влияние. Существующие в настоящее время модели этого не
делают. Влияние гарнисажа на процесс кристаллизации
металла устраняется либо заданием коэффициентов теплопередачи по высоте, либо
заданием теплового потока на границе металла и шлака. В обоих случаях в решение
задачи вводятся заведомо неизвестные характеристики, что приводит к
необъективности математической модели. Причем, при стремлении упростить решение
задачи моделирования процессов кристаллизации слитка, многие исследователи
рассматривают плоскопараллельные, стационарные модели, которые в принципе не
могут хорошо описать изучаемые явления. Следует отметить, что все известные в
литературе модели и алгоритмы контроля и управления тепловыми процессами в
кристаллизаторе МНЛЗ получены путем вышеуказанных упрощений, и, следовательно,
имеют ограниченную область применения. В связи с этим исследование, связанное с
построением модели охлаждения слитка в кристаллизаторе, с учетом влияния
шлаковой прослойки представляется актуальным.
Кроме того, разработка методики решения нестационарной, пространственной задачи Стефана представляет большой научный
интерес, так как расширяет возможности решения очень сложных краевых задач,
связанных с фазовыми переходами.
При построении математической модели
процесса затвердевания слитка и водяного охлаждения стенки кристаллизатора
необходимо решить следующие задачи:
1.
Построить
трехмерную нестационарную математическую модель затвердевания непрерывнолитого слитка и водяного охлаждения стенки
кристаллизатора, с учетом теплофизических процессов;
2.
Адаптировать
модели, с учетом влияния выбора ШОС и, следовательно, образуемого гарнисажа на тепловые потоки;
3.
Апробировать
разработанную математическую модель, используя экспериментальные данные,
приведенные в литературе;
4.
Изучить
влияние различных факторов на тепловые поля в слитке и стенке кристаллизатора;
5.
Обосновать
выбор теплотехнических режимов литья в непрерывнолитые
заготовки.
Обобщенное уравнение
теплопроводности и его безразмерная формулировка в виде (условные обозначения
всех величин приведены в конце):
![]() (1)
(1)
где:
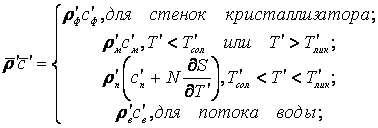 ,
,
 .
.
Причем ![]() , что следует из того факта, что при уменьшении температуры
доля жидкой составляющей в объеме расплава уменьшается от 1 (жидкая фаза) до 0
(твердая фаза).
, что следует из того факта, что при уменьшении температуры
доля жидкой составляющей в объеме расплава уменьшается от 1 (жидкая фаза) до 0
(твердая фаза).

В
дальнейшем, для упрощения, штрихи будут опускаться.
Приведя начальные и граничные
условия к безразмерному виду, получим:
·
начальная
температура равна температуре перегрева ![]() жидкого металла:
жидкого металла:
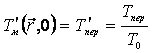 ;
(2)
;
(2)
·
температура
сплава на поверхности зеркала металла ![]() равна температуре
перегрева
равна температуре
перегрева ![]() :
:
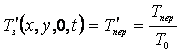 ;
(3)
;
(3)
·
на
нижней кромке кристаллизатора ![]() тепловой поток
отсутствует:
тепловой поток
отсутствует:
![]() ;
(4)
;
(4)
·
на
границе внутренней поверхности кристаллизатора и наружной поверхности отливки ![]() или
или ![]() соблюдается равенство
уходящего и входящего потоков тепла:
соблюдается равенство
уходящего и входящего потоков тепла:
![]() и
и ![]() ;
(5)
;
(5)
·
Для
плоскостей симметрии слитка xOz и yOz, проходящих через центр слитка,
тепловые потоки равны 0:
![]() и
и 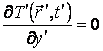 .
(6)
.
(6)
Отметим, что на внешней поверхности
слитка, граничащей со стенкой кристаллизатора, задан тепловой поток, значения
которого взяты из литературы.
Применяя метод конечных элементов к
системе дифференциальных уравнений (1–6) получим соответствующие дискретные
аппроксимирующие уравнения. Полученная после выполнения всех необходимых
процедур система уравнений решалась методом релаксации.
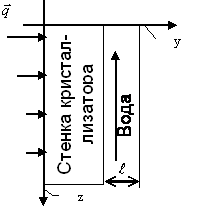 Система дифференциальных уравнений,
описывающих водяное охлаждение стенки кристаллизатора, после анализа литературных данных,
принято следующее упрощение: вода протекает по узкой щели и омывает стенку
сплошным потоком. На рисунке приведена принципиальная схема водяного
охлаждения. Необходимую толщину щели можно определить по формуле:
Система дифференциальных уравнений,
описывающих водяное охлаждение стенки кристаллизатора, после анализа литературных данных,
принято следующее упрощение: вода протекает по узкой щели и омывает стенку
сплошным потоком. На рисунке приведена принципиальная схема водяного
охлаждения. Необходимую толщину щели можно определить по формуле: ![]() , где
, где ![]() – расход воды в
секунду;
– расход воды в
секунду; ![]() – средняя скорость
воды в канале;
– средняя скорость
воды в канале; ![]() – периметр
охлаждаемого слитка. Скорость
– периметр
охлаждаемого слитка. Скорость ![]() определяется по
формуле:
определяется по
формуле: ![]() , где
, где ![]() – площадь сечения всех
каналов. На внутренней (горячей) стороне стенки задан тепловой поток
– площадь сечения всех
каналов. На внутренней (горячей) стороне стенки задан тепловой поток ![]() из слитка, который
передается в воду.
из слитка, который
передается в воду.
Приведя
начальные и граничные условия к безразмерному виду, получим следующие
соотношения:
·
Температура
стенок кристаллизатора в начальный момент времени равна температуре охлаждающей
воды на входе:
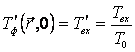 . (7)
. (7)
·
На
поверхностях ![]() и
и ![]() : на уровне верхней и нижней кромки стенки
кристаллизатора
: на уровне верхней и нижней кромки стенки
кристаллизатора ![]() и
и ![]() тепловой поток
отсутствует:
тепловой поток
отсутствует:
![]() .
(8)
.
(8)
·
На
поверхности ![]() : на границе внутренней поверхности кристаллизатора и
наружной поверхности отливки
: на границе внутренней поверхности кристаллизатора и
наружной поверхности отливки ![]() соблюдается равенство
уходящего и входящего потоков тепла:
соблюдается равенство
уходящего и входящего потоков тепла:
![]() .
(9)
.
(9)
·
На
поверхности ![]() : на границе внешней поверхности кристаллизатора и потока
воды
: на границе внешней поверхности кристаллизатора и потока
воды ![]() соблюдается равенство
уходящего и входящего потоков тепла, а также равенство температур стенки и
воды:
соблюдается равенство
уходящего и входящего потоков тепла, а также равенство температур стенки и
воды:
![]() ;
(10)
;
(10)
![]()
·
Для
плоскости yOz, проходящей через центр, и у
боковой поверхности слитка, имеет место равенство нулю тепловых потоков:
![]() .
(11)
.
(11)
Для потока воды, омывающего наружную
поверхность кристаллизатора, имеем следующие граничные условия:
·
На
поверхности ![]() , т. е. в точке подачи охлаждающей воды
, т. е. в точке подачи охлаждающей воды ![]() задана температура
воды на входе
задана температура
воды на входе ![]() , при этом:
, при этом:
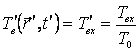 . (12)
. (12)
·
На
внешней границе водяного потока ![]() тепловой поток
отсутствует:
тепловой поток
отсутствует:
![]() .
(13)
.
(13)
·
На
поверхности ![]()
![]() и на боковых
поверхностях тепловой поток равен нулю:
и на боковых
поверхностях тепловой поток равен нулю:
![]() и
и ![]() .
(14)
.
(14)
При расчете
водяного охлаждения предлагается использовать следующий алгоритм:
1.
Вычисляем
тепловое поле стенки кристаллизатора. На границе с водой задан тепловой поток в
виде: ![]() , где скорость определяется по величине теплового потока. При
этом неявно будет выполняться равенство температур стенки кристаллизатора и
воды, если принять:
, где скорость определяется по величине теплового потока. При
этом неявно будет выполняться равенство температур стенки кристаллизатора и
воды, если принять: ![]() .
.
2.
Вычисляем
поле температур в воде. При этом на границе задается равенство тепловых
потоков, то есть: ![]() . Толщина вязкого подслоя и скорость на его границе
определяются по формулам, приведенным в литературе.
. Толщина вязкого подслоя и скорость на его границе
определяются по формулам, приведенным в литературе.
3.
Для
окончания итерационного процесса используется условие равенства количества
тепла поступившего в кристаллизатор и количества тепла отведенного с водой: ![]() , где:
, где: ![]() – внутренняя (горячая) поверхность стенки
кристаллизатора;
– внутренняя (горячая) поверхность стенки
кристаллизатора; ![]() – область, заполненная
водой. Количество тепла, отведенного с водой, зависит от степени турбулизации потока, которая будет определяться
турбулентной теплопроводностью
– область, заполненная
водой. Количество тепла, отведенного с водой, зависит от степени турбулизации потока, которая будет определяться
турбулентной теплопроводностью ![]() . Значение
. Значение ![]() необходимо получить в
ходе вычислительного эксперимента.
необходимо получить в
ходе вычислительного эксперимента.
Профиль
скоростей в потоке задан следующим образом:
·
на
границе с водой ![]() ;
;
·
на
границе ламинарного подслоя, толщина которого ![]() , скорость равна
, скорость равна ![]() ;
;
·
в
остальной части потока скорость равна средней скорости потока:
![]() ;
;
·
кроме
того, на границе кристаллизатора с водой, из-за значительного теплового напора,
возникают конвективные вихри, поэтому составляющая скорости ![]() .
.
Для
определения зависимости ![]() использовались
результаты, приведенные в литературе, описывающие зависимость температуры холодной
стороны стенки от теплового потока. На основе данных получены зависимости,
приведенные на диаграмме:
использовались
результаты, приведенные в литературе, описывающие зависимость температуры холодной
стороны стенки от теплового потока. На основе данных получены зависимости,
приведенные на диаграмме:
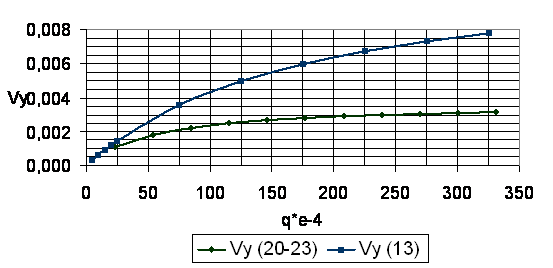
Здесь
в скобках указана толщина стенки кристаллизатора в мм.
Результаты
расчета тепловых полей слитка и водяного охлаждения кристаллизатора. Из анализа
полученных результатов следует, что при тепловых потоках, значения которых
приводятся в литературе, поверхность слитка сильно переохлаждается. Слиток
имеет следующие параметры: температура поверхности лежит в диапазоне 700–1000 oC; толщина корочки слитка от 35 – 57
мм. В литературе приводятся экспериментальные значения температуры поверхности
слитка на выходе из кристаллизатора, значительно отличающиеся от температур
полученных при расчетах: температура > 1150 oC, а толщина корочки в пределах 30 –
40 мм. Это говорит о том, что значения тепловых потоков должны быть меньше.
По–видимому, различие связанно с тем, что приводятся значения потоков,
возникающие в нестандартном режиме работы кристаллизатора, например, при
прорыве металла. В нормальном режиме тепловые потоки меньше.
Определяющими характеристиками
шлаковых расплавов приняты следующие:
·
 температура плавления;
температура плавления;
·
коэффициент
теплопроводности, при различных температурах;
·
вязкость
при температурах зеркала металла и поверхности слитка на выходе из
кристаллизатора;
·
удельный
расход;
·
плотность
расплава;
·
и
другие.
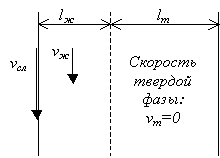
При определении толщины ганисажа
принимается допущение о том, что толщина гарнисажа не
изменяется по высоте слитка. На рисунке приведена принципиальная схема
структуры шлаковой прослойки, образующаяся при вытягивании слитка со скоростью ![]() . Жидкая часть прослойки движется с некоторой скоростью
. Жидкая часть прослойки движется с некоторой скоростью ![]() . На границе, контактирующей со слитком, задана температура,
равная температуре слитка:
. На границе, контактирующей со слитком, задана температура,
равная температуре слитка: ![]() . На другой границе задана температура внутренней стенки
кристаллизатора:
. На другой границе задана температура внутренней стенки
кристаллизатора: ![]() . На границе раздела жидкой и твердой фаз гарнисажа
температура равна температуре затвердевания шлака:
. На границе раздела жидкой и твердой фаз гарнисажа
температура равна температуре затвердевания шлака: ![]() . Отсюда, используя равенство тепловых потоков, нетрудно
получить толщину затвердевшей части гарнисажа:
. Отсюда, используя равенство тепловых потоков, нетрудно
получить толщину затвердевшей части гарнисажа:
![]() (15)
(15)
здесь
принято: ![]() и
и ![]() .
.
Толщину жидкой прослойки гарнисажа можно косвенно определять по усилию вытягивания,
расходу ШОС и её физико-химическим характеристикам. Расход ШОС можно определить
по формуле:
![]() (16)
(16)
Вторым уравнением для определения
толщины жидкой прослойки, является уравнение для силы вязкого трения:
![]() (17)
(17)
Для
решения системы уравнений (16–17) использовались средства MS Excel 2000. Из анализа данных, полученных
при исследовании влияния различных факторов на толщину прослойки, следует, что
толщина жидкой прослойки шлака находится в интервале 0,05–0,35 мм, что хорошо согласуется с
экспериментальными данными. Рекомендуемая в литературе оптимальная
толщина гарнисажа 0,15–0,23 мм. Скорость жидкой составляющей ШОС ![]() , при скорости разливки 1
м/мин, равна 0,6–1,0 м/мин.
, при скорости разливки 1
м/мин, равна 0,6–1,0 м/мин.
При исследовании влияния параметров
ШОС на разливку, наиболее важными характеристиками ШОС, влияющими на разливку
металла являются:
·
Температура
затвердевания ШОС;
·
Теплопроводность
гарнисажа;
·
Толщина
жидкой прослойки, методика расчета которой была приведена выше.
Теперь принимая, что в условии (5)
на широкой грани слитка ![]() , тепловой поток задан в виде:
, тепловой поток задан в виде:
![]() (18)
(18)
Температура холодной стороны ![]() заданна как функция
теплового потока из слитка и толщины кристаллизатора. Температура горячей
стороны кристаллизатора Tгор вычисляется по формуле:
заданна как функция
теплового потока из слитка и толщины кристаллизатора. Температура горячей
стороны кристаллизатора Tгор вычисляется по формуле:
![]() (19)
(19)
В заключении вводится допущение, что
на узкой грани слитка тепловой поток ![]() симметричен
относительно ребра слитка:
симметричен
относительно ребра слитка:
![]() (20)
(20)
где: ![]() – тепловые потоки из
слитка; а
– тепловые потоки из
слитка; а ![]() – расстояние от ребра
слитка.
– расстояние от ребра
слитка. 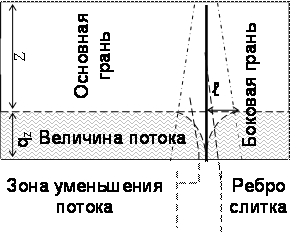 Допущение о симметричности тепловых потоков
относительно ребра слитка обосновывается расчетами. Отметим, что допущение о симметричности тепловых потоков относительно
ребра слитка представляется достаточно обоснованным. Известно, что на боковой
поверхности слитка теплоотвод меньше, чем на основной
грани примерно на 15–20%. Рассмотрим рисунок, здесь на расстоянии z от уровня зеркала металла изображен
тепловой поток qz. На расстоянии ℓ от ребра слитка,
тепловой поток начинает уменьшаться практически до 0. Это
связанно с тем, что на ребре слитка отвод тепла осуществляется по двум
направлениям, в результате чего температура поверхности слитка стремится к
температуре затвердевания ШОС, то есть
Допущение о симметричности тепловых потоков
относительно ребра слитка обосновывается расчетами. Отметим, что допущение о симметричности тепловых потоков относительно
ребра слитка представляется достаточно обоснованным. Известно, что на боковой
поверхности слитка теплоотвод меньше, чем на основной
грани примерно на 15–20%. Рассмотрим рисунок, здесь на расстоянии z от уровня зеркала металла изображен
тепловой поток qz. На расстоянии ℓ от ребра слитка,
тепловой поток начинает уменьшаться практически до 0. Это
связанно с тем, что на ребре слитка отвод тепла осуществляется по двум
направлениям, в результате чего температура поверхности слитка стремится к
температуре затвердевания ШОС, то есть ![]() . Для оценки влияния зоны на средние потоки из граней,
примем, что в приреберной зоне уменьшение среднего
потока примерно равно
. Для оценки влияния зоны на средние потоки из граней,
примем, что в приреберной зоне уменьшение среднего
потока примерно равно ![]() . Для
определенности примем следующие размеры слитка:
. Для
определенности примем следующие размеры слитка:
·
основная грань – 1,5 м;
·
боковая грань – 0,2 м;
·
высота кристаллизатора – 1м;
·
средняя ширина зоны уменьшения
потока – 0,025 м. Отметим, что литературе приводятся сведения, что ширина ℓ зоны
повышенного износа стенок достигает до 70 мм. Таким образом, принятое значение
средней толщины зоны вполне обосновано.
Пусть средний поток из слитка равен 1000 кДж/(м2*с), тогда средний поток в зоне уменьшения
потока будет равен 500 кДж/(м2*с). Ниже в таблице приведены расчеты
количества тепла поступающего из каждой грани слитка, для принятых значений.
|
|
Основная грань |
Боковая грань |
||
|
Плошадь (м2) |
Количество тепла (кДж) |
Плошадь (м2) |
Количество тепла (кДж) |
|
|
Исходный
поток |
1,5 |
1500 |
0,2 |
200 |
|
Без зоны |
1,45 |
1450 |
0,15 |
150 |
|
В зоне |
0,05 |
25 |
0,05 |
25 |
|
Всего |
1475 |
175 |
||
Теперь нетрудно
подсчитать средние потоки по каждой грани и их изменение. Отметим, что
изменение значения среднего потока из слитка никак не будет влиять на
относительное изменение средних потоков из граней слитка.
|
Изменение
ср. потока |
Всего из слитка |
Основная грань |
Боковая грань |
|
Абсолютное (кДж/(м2*с)) |
971 |
983 |
875 |
|
Относительное
(%) |
97,1 |
98,3 |
87,5 |
Из
таблицы следует, что при средней ширине зоны 25 мм, относительное изменение среднего
потока с боковой грани, относительно основной достигает 12–13%. Причем, при
увеличении средней ширины зоны относительное изменение потоков будет
возрастать.
В четвертом параграфе
исследовались критерии оптимальности непрерывной
разливки металла, которые вводятся на основании качественных рекомендаций о
желательном распределении температуры в затвердевающем непрерывном слитке. Предполагается, что слитки с лучшими
температурными полями характеризуются меньшими значениями критериев и более
высоким качеством. В работе рассмотрены следующие критерии:
·
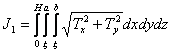 – критерий вводится,
исходя из требований небольших градиентов температуры по толщине корочки;
– критерий вводится,
исходя из требований небольших градиентов температуры по толщине корочки;
·
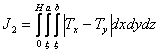 – критерий определяет
равномерность теплоотвода в поперечном сечении внутри
корочки слитка;
– критерий определяет
равномерность теплоотвода в поперечном сечении внутри
корочки слитка;
·
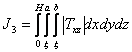 ,
, 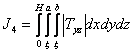 – критерии вводятся,
исходя из рекомендаций о желательности приблизительной прямолинейности
распределения кривых температуры в продольном сечении затвердевающей части
слитка;
– критерии вводятся,
исходя из рекомендаций о желательности приблизительной прямолинейности
распределения кривых температуры в продольном сечении затвердевающей части
слитка;
·
![]() – критерий определяет
интенсивность продольного переноса тепла на боковой поверхности.
– критерий определяет
интенсивность продольного переноса тепла на боковой поверхности.
Анализ результатов расчетов
показывает, что оптимальным является режим разливки под ШОС, имеющей большую
толщину жидкой фазы, температуру затвердевания и меньшую теплопроводность. Это
означает, что при разливке металла оптимальными будут режимы с меньшими
потоками тепла из слитка и, следовательно, меньшими перепадами температур в корочке
слитка.
Ниже приведены сравнительные данные
расчетов для наиболее и наименее оптимального режима разливки. Под наиболее
оптимальным режимом будем понимать режим, при котором значения критериев
минимальны. Наименее оптимальный режим будет при максимальных значениях
критериев. В таблице приведены средние значения, полученные по результатам
расчетов.
Средние значения
|
Наименование |
Min |
Max |
|
Поток, при L=1000 мм |
308 кДж/(м2*с) |
842 кДж/(м2*с) |
|
Поток, при L=600 мм |
356 кДж/(м2*с) |
995 кДж/(м2*с) |
|
Средняя температура |
1385 oС |
1050 oС |
|
Средняя толщина корочки слитка |
19 мм |
29 мм |
Здесь L – длина кристаллизатора.
Анализ данных показывает, что при
увеличении потоков в 3 раза толщина корочки увеличивается в 1,5 раза. При этом значения
критериев оптимальности увеличиваются в 4–7 раз, что приведет к снижению
качества поверхности слитка, что крайне не желательно. Установление связи между
качеством поверхности слитка и значениями критериев оптимальности выходит за
рамки работы, но представляет несомненный интерес.
По результатам расчетов сделаны
следующие выводы:
1.
Выбор
ШОС существенно влияет на тепловое состояние стенки кристаллизатора.
Максимальная толщина рабочей поверхности стенки зависит от характеристики
используемой ШОС и может колебаться от 20 до 50 мм. Правильный выбор ШОС
позволит существенно увеличить срок эксплуатации кристаллизатора.
2.
Скорость
разливки является одним из самых важных параметров разливки. Подбором
параметров ШОС можно повысить скорость разливки до 1,5 м/мин, что позволит
повысить качество слитков.
3.
Параметры
разливаемого металла, в частности теплопроводность, имеют меньшую значимость
при разливке. Но их влияние необходимо учитывать, так как они влияют на толщину
корочки на выходе из кристаллизатора.
Основные обозначения:
![]()
![]() – температура;
– температура;
![]()
![]() – удельная
теплоемкость;
– удельная
теплоемкость;
![]()
![]() – удельная плотность;
– удельная плотность;
![]()
![]() – коэффициент
теплопроводности;
– коэффициент
теплопроводности;
![]()
![]() – удельная теплота
плавления;
– удельная теплота
плавления;
![]()
![]() – скорость движения
частицы;
– скорость движения
частицы;
![]() – оператор Гамильтона;
– оператор Гамильтона;
![]() – параметр агрегатного
состояния, соответствующий объемной доле жидкой фазы в двухфазной зоне
– параметр агрегатного
состояния, соответствующий объемной доле жидкой фазы в двухфазной зоне ![]() . Зависимость
. Зависимость ![]() определяется по
равновесной диаграмме конкретного материала;
определяется по
равновесной диаграмме конкретного материала;
![]() ,
, ![]() ,
, ![]() – индексы, указывающие
коэффициенты для: стенок формы, некристаллизующегося металла и переходной зоны
соответственно;
– индексы, указывающие
коэффициенты для: стенок формы, некристаллизующегося металла и переходной зоны
соответственно;
![]() – критерий Фурье;
– критерий Фурье;
![]() – критерий гомохромности;
– критерий гомохромности;
![]() – критерий,
характеризует процесс затвердевания;
– критерий,
характеризует процесс затвердевания;
![]() – скорость вытягивания
слитка;
– скорость вытягивания
слитка;
![]() – скорость подачи
воды;
– скорость подачи
воды;
![]() – периметр слитка;
– периметр слитка;
![]() – скорость движения ШОС в зазоре;
– скорость движения ШОС в зазоре;
![]() – толщина жидкой шлаковой прослойки;
– толщина жидкой шлаковой прослойки;
![]() – высота слитка массой 1 т;
– высота слитка массой 1 т;
![]() – плотность ШОС;
– плотность ШОС;
![]() – вязкость смазки;
– вязкость смазки;
![]() – площадь поверхности;
– площадь поверхности;
![]() – скорость перемещения
трущихся поверхностей;
– скорость перемещения
трущихся поверхностей;
![]() – температура горячей
поверхности стенки кристаллизатора;
– температура горячей
поверхности стенки кристаллизатора;
![]() – теплопроводность
ШОС;
– теплопроводность
ШОС;
![]() – температура
поверхности слитка;
– температура
поверхности слитка;
![]() – температура
затвердевания ШОС;
– температура
затвердевания ШОС;
![]() – толщина жидкой
прослойки;
– толщина жидкой
прослойки;
![]() – тепловой поток из
слитка;
– тепловой поток из
слитка;
![]() – толщина
кристаллизатора;
– толщина
кристаллизатора;
![]() – теплопроводность
материала стенки кристаллизатора.
– теплопроводность
материала стенки кристаллизатора.