Èñõîäíûé URL: http://vasculograph.narod.ru/article.rar
Computer generated models of intraorgan arterial beds: hydraulic conductivity and input admittance
1 Department of Theoretical Mechanics
V.N.Karazin Kharkiv National University,
Svobody Sq.,4, 61077 Kharkov, Ukraine
nnk_@bk.ru
2 Department of Human Anatomy
Donetsk National Medical University,
Illicha St., 16, 83003 Donetsk, Ukraine
Abstract. Geometry of the arterial junctions is investigated on the plastic casts of the human intraorgan arterial vasculatures. Some statistical dependence between the lengths and diameters of the arterial segments are revealed. On the basis of the observed regularities for different inner organs the software for generation and visualization of the realistic models of the intraorgan arterial beds is elaborated. Pressure wave propagation in the generated branching systems of viscoelastic tubes is investigated.
1 Introduction
Geometry of the arterial intraorgan vasculatures defines
blood supply to the organ and blood redistribution between the organs [1-2]. Structure-function
relationships in the vascular beds are strongly influenced by their geometry
[3]. The diameters and lengths of separate arterial segments and branching
angles in junctions can be measured on the plastic casts of the arterial beds. The
results of the measurements can be used for direct calculations of the
hydraulic conductivity Z and wave input admittance of the vasculatures. Traditionally, the input impedance 
or input admittance
has
been used to characterize the dynamic properties of the arterial systems [4].
The input admittance is defined as the relationship of flow Q(t) and pressure P(t)
at the entrance of the arterial bed and describes the ability of the arterial
system for passive impeding the blood flow as well as active regulation of the
wave propagation through the vasculature [5]. The data include a few thousand
values that characterize geometry of the investigated vasculature only [6-8]. Arterial
beds of different inner organs possess different topology and undergo significant
individual variations. Physiological variations of the lengths (
) and
diameters (
) of arterial segments cause noticeable
differences in the conductivity of the arterial systems of a given inner organ
in different individuals.
The measurements on the casts have revealed the following regularities in geometry of the arterial bifurcations [9-11]:
· Murray law 
(1)
· 
(2)
|
|
|
|
a |
b |
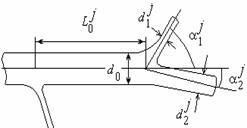
Fig. 1. Parameters of a separate bifurcation (a) and a subsystem of the arterial network.
where 
, 
are the diameters
of the daughter and parent vessels in the j-th junction, 
are
branching angles (fig.1a,b). Taking into account the regularities the realistic
models of arterial vasculatures can be constructed on the basis of a given set
of the parameters 
where 
is the diameter of the
feeding artery of the vasculature, 
is an asymmetry coefficient. When the
parameters 
are constant for all the junctions the
model of the arterial vasculature as a self-similar
tree-like system of compliant tubes can be constructed and used for calculations
the hydraulic properties and the pressure wave propagation in the system taking
into consideration wave reflection at bifurcations [12-14]. The models have
been found to be very useful for biomechanical interpretation of the pulse wave
curves P(t), Q(t) as an important tool for medical diagnostics [14-16]. The
differences in geometry of the arterial beds of different inner organs have not
been embedded into the fractal models yet.