Abstract: In this paper, a new dynamic data allocation algorithm for non-replicated distributed database systems (DDS), namely the NNA algorithm, is proposed. This algorithm reallocates data with respect to changing data access pattern for each fragment. In this algorithm, data is moved to a node which is the neighborhood and also placed in the path to the node with maximum access counter. This algorithm is very suitable for DDS in the networks which have low bandwidth and frequent requests for a data fragment come from different sites by providing data clustering. The simulation results show that for complex and large networks where the request for fragments generates more frequently or the fragment size is large, the NNA algorithm provides better response time and spends less time for moving fragments in the network.
Developments in database and networking technologies in the past few decades led to advances in distributed database systems. A DDS is a collection of sites connected by a communication network, in which each site is a database system in its own right, but the sites have agreed to work together, so that a user at any site can access data anywhere in the network exactly as if the data were all stored at the user's own site [11]. The primary concern of a DDS is to design the fragmentation and allocation of the underlying database. Fragmentation unit can be a file where allocation issue becomes the file allocation problem. File allocation problem is studied extensively in the literature, started by Chu [12] and continued for non-replicated and replicated models [13, 14]. Some studies considered dynamic file allocation [15, 16].
Various approaches have already been described the data allocation technique in distributed systems. Some methods are limit in their theoretical and implementation parts. Other strategies are ignoring the optimization of the transaction response time. The other approaches present exponential time of complexity and test their performance on specific types of network connectivity.
Data allocation problem was introduced when Eswaran [17] first proposed the data fragmentation. Studies on vertical fragmentation [18, 19]; horizontal fragmentation [20] and mixed fragmentation [21] were conducted. The allocation of the fragments is also studied extensively.
In these studies, data allocation has been proposed prior to the design of a database depending on some static data access patterns and/or static query patterns. In a static environment where the access probabilities of nodes to the fragments never change, a static allocation of fragments provides the best solution. However, in a dynamic environment where these probabilities change over time, the static allocation solution would degrade the database performance. Initial studies on dynamic data allocation give a framework for data redistribution and demonstrate how to perform the redistribution process in minimum possible time. In [3] a dynamic data allocation algorithm for non-replicated database systems is proposed named optimal algorithm, but no modeling is done to analyze the algorithm. In [5] the threshold algorithm is proposed for dynamic data allocation algorithm which reallocates data with respect to changing data access patterns and focused on load balancing issue.
A major cost in executing queries in a distributed database system is the data transfer cost incurred in transferring relations (fragments) accessed by a query from different sites to the site where the query is initiated. The objective of a data allocation algorithm is to determine an assignment of fragments at different sites so as to minimize the total data transfer cost incurred in executing a set of queries. This is equivalent to minimizing the average query execution time, which is of primary importance in a wide class of distributed conventional as well as multimedia database systems.
In this paper we are going to present and analyze a new approach for dynamic data allocation algorithm named Near Neighborhood Allocation. This algorithm is based on optimal algorithm, but with different strategy for selecting nodes for data movements. The rest of this paper is organized as following: In section 2 we will describe about our method, section 3 is consists of our simulation environment and its results and section 4 is our conclusion.
Our NNA algorithm is based on optimal algorithm. In optimal algorithm initially, all fragments are distributed over the nodes according to any method. Afterwards, any node j, runs the optimal algorithm described as following for every fragment I, that it stores.
(1) For each (locally) stored fragment, initialize the access counter rows to zero. (S = 0 ik were k = 1,..,n)
(2) Process an access request for the stored fragment
(3) Increase the corresponding access counter of the accessing node for the stored fragment. (If node x accesses fragment I, set Six = Six +1)
(4) If the accessing node is the current owner, go to step 2. (i.e Local access, otherwise it is a remote access)
(5) If the counter of a remote node is greater than the counter of the current owner node, transfer the ownership of the fragment together with the access counter array to the remote node. (i.e fragment migrates) (If node x accesses fragment I and Six > Sij , send fragment I to node x)
(6) Go to step 2.
The problem of this approach is that if the changing frequency of access pattern for each fragment is high, it will spend a lot of time for transferring fragments to different nodes. So, the response time and delay will be increased.
In our algorithm, we are going to address the problem of optimal algorithm:
In NNA algorithm, the requirement for moving a fragment is obtained as in optimal algorithm. But, the destination of moved data is different. In our method we consider the network topology and routing for specifying destination. In other words the destination of the moved fragment is the neighbor of the source which is exists in the path from the source to the node with highest access pattern. Any routing algorithm can be used but we use link-state routing algorithm.
By using this approach we avoid from frequently moving data because finally the fragment will be placed in a node which has average access cost for nodes that using it. So, delay of movement will be reduced. Furthermore, the response time also will be improved.
Another aspect of NNA algorithm is that the fragments which are used by a node or neighbors of a node can be clustered. By using this clustering we can effectively respond to the requests.
For example according to the Figure 1 assume that node G, H, I and E frequently send a request for a fragment i which is on the node A. According to our algorithm, after that number of requests exceeded from the predefined threshold, we move the fragment i to node C. If the requests are continued after fragment migration, we move the fragment to node B. This approach will be continued until the fragment reaches to node G. By placing the fragment on node G, the requests from G, H, I and E will be responded with less delay but not with minimum delay. In this step, data is in a stable state. After this step, if one of the nodes H, G and E request the data more frequently than the other nodes, the fragment will be placed in it. By sending the fragment to the nodes that request it with the predefined threshold, the data will be migrated frequently from one node to the other node and it takes a lot of time and also responses will be send by a lot of delay when the data is moving. Using NNA approach, avoids form these problems with trade off of providing less delay not minimum delay.
In this experiment, we used the topology shown in figure 1. Our routing is based on link cost using Dijkstra algorithm (Shortest Path First). In our experiment links cost can change over simulation. So our system has 9 nodes as shown below. In standard mode our system has 4 nodes as active nodes to send queries. A, C, D and H are active nodes. A's Rate is 0.5 of others in all of experiments. Simulation length is 20000 cycle. Activation is from 0 to 10000.
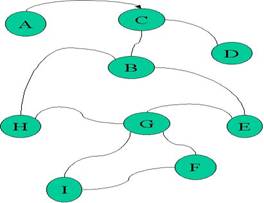
Figure1 The topology of the experiment
In our experiments, we consider two factors: average delay for receiving the response for a fragment request and average time spent for moving data from one node to the other node. We will investigate the effect of different parameters on these factors.
Fragment Size
Figure 2 and 3 show the effect of fragment size on these factors. As can be seen form Figure 2, we show the linear approximation for the effect of fragments size on the delay of response to a query. As can be seen there is a threshold value (near 8000 Byte) that defines the situations each algorithm performs better than the other one. For fragments less than 8000 bytes optimal algorithm is better and when fragments in the DDB are larger than 8000 bytes, NNA is preferred. In different networks this threshold may be different. But we can generally conclude that for large fragments NNA performs better.
According for Figure 3, for small fragments the average time spent for moving data in NNA algorithm is larger than optimal algorithm and for larger fragments it is reversed. Its reason is that for small fragments the cost of moving data to destination node is low and so, the movement cost is not exceeded to access cost. In the case of large fragments the movement of fragments takes a lot of time and also increased the network traffic. So, less movement will produce a lot of advantages that overcomes to the access cost.

Figure 2 Effect of fragment size on the delay of responding to a fragment request in optimal and NNA approach
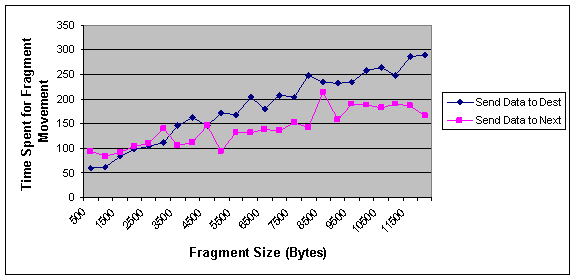
Figure 3 Effect of fragment size on the average time spent for moving fragments in optimal and NNA approach
Query Production Rate
Figure 4 and 5 shows the effect of query production rate on our factors. As can be seen if the rate of query is increased, the delay of response and also average time for fragment movement is decreased. Because the high rate of query causes each fragment find its proper owner node and stays on it sooner. So, the delay of response for a fragment will be decreased.
As shown, NNA algorithm except the situation where the rate of query production is very low, in other situations performs better than optimal algorithm.
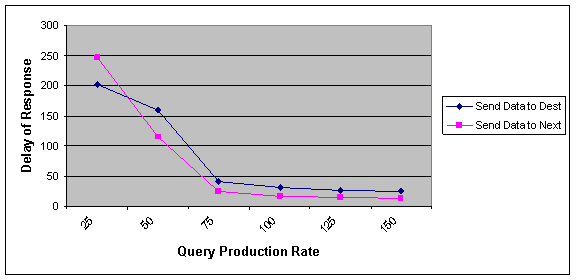
Figure 4 Effect of query production rate on the delay of responding to a fragment request in optimal and NNA approach
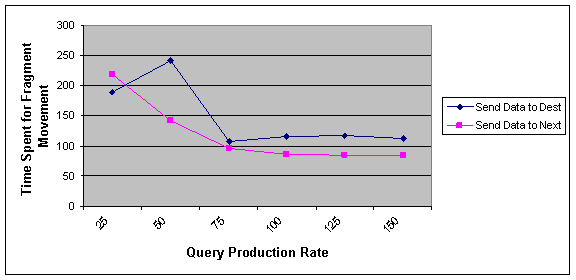
Figure 4 Effect of query production rate on the average time spent for moving fragments in optimal and NNA approach
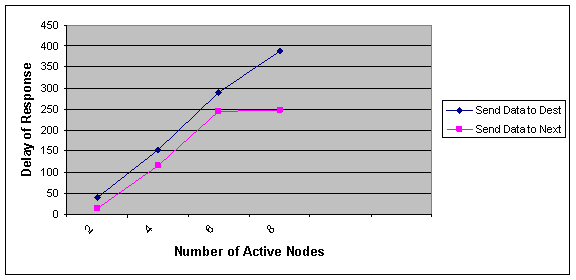
Number of Active Nodes
As shown in Figure 5, as the number of nodes in our network increases, the difference between optimal and NNA algorithm is appeared well. In our experiment we change the number of nodes form 2 to 8. According to the results we conclude that in larger networks NNA algorithm respond to a request with much lower delay than optimal algorithm. As shown in Figure 6 We can also predict that as the number of nodes indifferent networks the average time spent for moving fragments in NNA algorithm is less than optimal algorithm. But this conclusion needs to be experimented on more complex networks.

Figure 5 Effect of number of nodes in the network on the delay of responding to a fragment request in optimal and NNA approach

Figure 6 Effect of number of active nodes on the average time spent for moving fragments in optimal and NNA approach
In this paper we represented a new dynamic data allocation algorithm in DDB named Near Neighborhood Allocation (NNA) algorithm. This algorithm is based on optimal algorithm but the difference is in its approach for selecting destination node of moving fragments. In our experiments we consider two factors, average delay of responding to a fragment request and average time spent for moving fragments in the networks. We examine the effect of different parameters on these factors. Findings of our experiments indicate that for larger fragment size and query production rate, the NNA algorithm performs better and for small fragment size and query production rate the optimal algorithm performs better. The threshold for fragment size is almost 8000 bytes. For larger networks, by using NNA algorithm we can decrease the delay of response to a fragment regarding to optimal algorithm.
[1]L. C. John, A Generic Algorithm for Fragment Allocation in Distributed Database Systems, ACM, 1994
[2] Ahmad, I., K. Karlapalem, Y. K. Kwok and S. K. Evolutionary Algorithms for Allocating Data in Distributed Database Systems, International Journal of Distributed and Parallel Databases, 11: 5-32, The Netherlands, 2002.
[3] A. Brunstroml, S. T. Leutenegger and R. Simhal, Experimental Evaluation of Dynamic I)ata Allocation Strategies in a Distributed Database with changing Workloads, ACM Transactions on Database Systems, 1995
[4] A. G. Chin, Incremental Data Allocation and ReAllocation in Distributed Database Systems, Journal of Database Management; Jan-Mar 2001 ; 12, 1; ABI/INFORM Global pg. 35
[5] T. Ulus and M. Uysal, Heuristic Approach to Dynamic Data Allocation in Distributed Database Systems, Pakistan Journal of Information and Technology 2 (3): 231-239, 2003 , ISSN 1682-6027
[6] S. Voulgaris, M.V. Steen, A. Baggio, and G. Ballintjn, Transparent Data Relocation in Highly Available Distributed Systems. Studia Informatica Universalis. 2002
[7] Navathe, S.B., S. Ceri, G. Wiederhold and J. Dou, Vertical Partitioning Algorithms for Database Design, ACM Transaction on Database Systems, 1984 , 9: 680-710.
[8] P.M.G. Apers, "Data allocation in distributed database systems," ACM Transactions on Database Systems, vol. 13, no. 3, pp. 263-304, 1988.
[9] Y. F. Huang and J. H. Chen, Fragment Allocation in Distributed Database Design Journal of Information Science and Engineering 17, 491-506, 2001
[10] I. O. Hababeh , A Method for Fragment Allocation Design in the Distributed Database Systems, The Sixth Annual U.A.E. University Research Conference, 2005
[11] T. ?zsu, and P. Valduriez, 1991. Principles of Distributed Database Systems. Prentice-Hall Book Co., Englewood Cliff, USA
[12] Chu, W.W., 1969. Optimal File Allocation in a Multiple Computer System, IEEE Transactions on Computers, C-18: 885-889.
[13] H.L. Morgan, and K.D. Levin, 1977. Optimal Program and Data Locations in Computer Networks, Communications of ACM., 20: 315-321.
[14] R.Azoulay-Schwartz, and S. Kraus, Negotiation on Data Allocation in Multi-Agent Environments, Autonomous Agents and Multi-Agent Systems, 5: 123-172, 2002.
[15] B.W. Wah, Data Management in Distributed Systems and Distributed Data Bases, Ph.D. Dissertation, University of California, Berkeley, CA, USA, 1979.
[16] A.J Smith, Long-term File Migration: Development and Evaluation of Algorithms, Communications of ACM, 24: 512-532. 1981.
[17] K.P Eswaran, Placement of Records in a File and File Allocation in a Computer Network, in Proceedings of IFIP Congress on Information Processing, Stockholm, Sweden, pp: 304-307. 1974.
[18] S.B.Navathe, S. Ceri, G. Wiederhold and J. Dou, Vertical Partitioning Algorithms for Database Design, ACM Transaction on Database Systems, 9: 680-710. 1984.
[19] S.Ceri, B.Pernici and G. Wiederhold, Optimization Problems and Solution Methods in the Design of Data Distribution, Information Systems, 14: 261-272. 1989.
[20] S.Ceri, S.B. Navathe and G. Wiederhold, Distribution Design of Logical Database Schemas, IEEE Transactions on Software Engineering, 9:487-503. 1983.
[21] Y.Zhang, and M.E. Orlowska, On Fragmentation Approaches for Distributed Database Design, Information Sci., 1: 117-132. 1994.