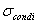 (R), where condi is the guard condition. So we can rebuild the original relation by union as follows:
(R), where condi is the guard condition. So we can rebuild the original relation by union as follows: Abstract.The execution process of the queries in distributed databases require accurate estimations and predictions for performance characteristics. The problems of data allocation and query optimization done by means of mobile agents and evolutionary algorithms are considered. These problems still present a challenge because of the dynamic changes in number of components
and architectural complexity of nowadays system topologies. The distributed system is modeled as a graph structure on which is defined a dynamic cost vector. The cost vector remains consistent, relevant, by use of mobile agents performing cost statistics and vector updates. An evolutionary technique for the re-design phase is proposed. Experimental results prove the efficiency of the proposed technique.
Keywords: Distributed Databases, Data Fragmentation, Data Allocation, Evolutionary Computation, Mobile agents.
Distributed databases (DDBs) have become necessity as networks expand and organizations perform geographically distributed operations. International companies store their data at different sites of a computer network, possibly in a variety of forms, ranging from flat files, to hierarchical, relational or object-oriented databases. The network itself consists of variety of transmission media, network topologies or network speeds. Design approaches for distributed databases have to consider various factors that can affect performance: CPU time, data transmission time, disk I/O operation time. Such distributed system architecture reveals some data management challenges. The system needs to be highly scalable with no critical failure points. In accordance to nowadays computing needs, the latency must not affect the performance of real-time applications. The aim is to provide uniform access to physically distributed data, no mater what the distance between the access location and places data resides. A possible approach is to represent the DDB as a graph and to perform system's management automatically by means of mobile agents. An evolutionary algorithm is proposed to solve the problem of re-fragmentation and re-allocation of data
Distributed database management system [8] has to ensure local applications for each computational component as well as global applications on more computational machines; it also has to provide a high-level query language with distributed query power, for distributed applications development. Must be ensured transparency levels that confer the image of a unique database. To improve the performance of global queries, data can be partitioned and spread over the system's components. A distributed database system supports data fragmentation if a relation stored within can be divided in pieces called fragments. These fragments can be stored on different sites residing on the same or different machines. The aim is to store the fragments closer to where they are more frequently used in order to achieve best performance. The partitions can be created horizontal, vertical or mixed (the combination of horizontal and vertical fragmentation).
Let R[A1,A2,...,An] be a relation where Ai, i=1,...,n are attributes. A horizontal fragment can be obtained by applying a restriction: Ri = 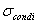 (R), where condi is the guard condition. So we can rebuild the original relation by union as follows:
(R), where condi is the guard condition. So we can rebuild the original relation by union as follows:
R = R1 U R2 U . . . U Rk.
A vertical fragment is obtained by a projection operation:
Ri=  (R),
(R),
{Ax1,Ax2,...,Axn}
where Axi, i=1,...,p are attributes. The initial relation can be reconstructed by join of the fragments:
R=R1 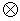 R2
R2 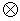 . . .
. . .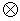 Rl.
Rl.
A DDB system can be represented [5] as a graph where the sites are given by (V), the set of vertices, and the edges (E) given by the direct connections between sites. Each edge has associated a cost, but this cost will be examined later in this paper. For exemplification we consider in Figure 1 a distributed system and obtain in Figure 2 the corresponding graph representation.

Figure 1. Distributed database system.
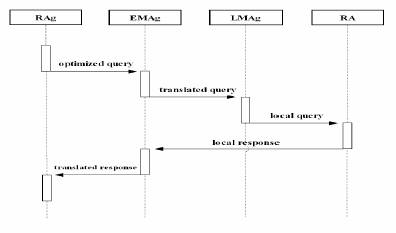
Figure 2. Corresponding graph of the system from Figure 1.
The system must preserve distributed data independence [9], such that any change of physical location of data must not disturb application functionality. A good management of DDBs implies a considerable effort in the design phase of the system and also implies a redesign phase for performance tuning. One of the design phase component that raise problems represent data fragmentation and allocation. The biggest improvement in system's response can be achieved by fragmentation and reallocation in the design refinement phase. The use of mobile agents can bring great performance value to the system because a software agent [10] can act autonomously on behalf of the administrator. The elements of the system do not have to be connected all the time, agents can travel in the network and execute at different hosts by taking their state and implementation with them. Agents can be intelligent, take decisions and react to environment changes to perform their actions, and most important, they can cooperate to fulfill their common goal.
In what follows, a distributed database system architecture where design relies on the graph representation and system management improvement by use of agents is proposed. An agent based architecture with distributed access and concurrent queries in heterogeneous database system is described. The considered architecture provides high scalability and performance optimization. The main improvement is the manner of cost definition between sites:
First, we de.ne the initial cost assigned by the system designer to an edge; this cost is estimated based on network transfer rate, data access time and computing power on a site. We call this initial estimated cost.
At some given times we can obtain more accurate cost in the system; we define this cost the up-to-date computed cost.
Translator agents perform the translation of local names to global names and provide a common language for distributed queries assuring local database management system independence.
Retriever agents collect data from corresponding fragments by communicating with Translators. In fact they build the query in the agent common language and ask the translators for results.
Optimizercan be unique for the entire system or can be cloned; it contains the query optimizer. One role of the Optimizer is to build up-to-date computed cost from statistics for the sites with respect to the amount of data accessed on that site.
The problem of database fragmentation and data allocation is modeled as a graph. We have to distribute m tuples to n nodes of the graph. The costs of the edges between the vertexes of the graph are given. Also, statistics referring to the frequency of the requested tuples in the graph are given (computed by agents). The tuples' distribution can be reduced to an optimization problem which goal is to minimize the costs generated by the queries in the graph. An evolutionary algorithm is proposed to solve this NP-Complete problem [6]. The proposed algorithm is called Evolutionary Fragmentation and Allocation Algorithm in Distributed Databases (EFA algorithm).
A fixed size population is used in the proposed algorithm. The m tuples that have to be distributed to nodes will be denoted by t1, t2,..., tm. There are no restrictions regarding the minimum or the maximum number of tuples contained by a node. A potential solution of the problem (a chromosome) is a string of constant length {x1, x2,...,xm}, where the gene xi, xi 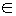 {1, 2,..., n}, indicates to which node the tuple i belongs.
{1, 2,..., n}, indicates to which node the tuple i belongs.
The potential solutions are evaluated by means of a real-valued fitness function F, F : X ->R, where X denotes the space of potential solutions. The fitness of a chromosome takes into account the costs of the edges between nodes and the statistics regarding the frequency of the requested tuples in the graph:
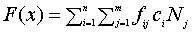 ,
,
where fij, i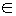 {1,2,...,n}, j
{1,2,...,n}, j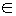 {1,2,...,m},represents the frequency of the requests of the tuple j from the node i of the graph. Also, ciNj, i
{1,2,...,m},represents the frequency of the requests of the tuple j from the node i of the graph. Also, ciNj, i 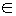 {1,2,...,n}, j
{1,2,...,n}, j 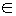 {1,2,...,m},, represents the cost of the edges between the node i and the node that contains the tuple j, denoted byNj . The fitness function F is to be minimized.
{1,2,...,m},, represents the cost of the edges between the node i and the node that contains the tuple j, denoted byNj . The fitness function F is to be minimized.
Rank-based selection for recombination mechanism [4], two points crossover and weak mutation operator [1] are considered for the proposed algorithm [3]. The best from parent and offspring enters the new generation [2].
The algorithm ends after a certain number of generations that did not improve the best solution of the generation [7]. The best solution obtained during the search process is considered to be the solution of the problem.
A graph having five nodes is considered (n = 5). Let us denote the five nodes by N1, N2, N3, N4, N5. The associated costs for the edges between the given nodes are depicted in Figure 4. Remark: We are interested only in the direct cost between two nodes, and that is why there are nodes without edges between them, even if there could be a path between the two nodes by using intermediate nodes.
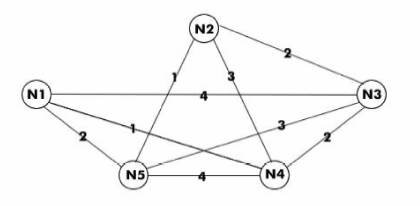
Figure 3. Proposed architecture.
A dataset of 1.200.000 tuples is given. The given tuples are denoted by t1, t2,..., tm., where m represents the number of tuples. The existing dataset fragmentation and distribution of tuples in nodes are depicted in the Table 1.
Table 1. Dataset fragmentation and distribution of tuples in nodes.
| Node | Dataset Fragmentation | Number of tuples/node |
| N1 | t1-t100.000 | 100.000 |
| N2 | t100.001-t380.000 | 280.000 |
| N3 | t380.001-t540.000 | 160.000 |
| N4 | t540.001-t720.000 | 180.000 |
| N5 | t720.001-t200.000 | 480.000 |
The statistics regarding the frequency of requests of the tuples from each node are depicted in Tables 2 - 6.
Table 2. The frequency of requests of the tuples from the node N1.
| Tuples | Frequency |
| t40.001-t90.000 | 4 |
| t420.001-t560.000 | 10 |
| t610.001-t730.000 | 12 |
| t980.001-t1.100.000 | 5 |
Table 3. The frequency of requests of the tuples from the node N2.
| Tuples | Frequency |
| t250.001-t330.000 | 2 |
| t560.001-t680.000 | 14 |
| t1.100.001-t1.200.000 | 7 |
Table 4. The frequency of requests of the tuples from the node N3.
| Tuples | Frequency |
| t1-t100.000 | 3 |
| t250.001-t290.000 | 10 |
| t880.001-t970.000 | 9 |
| t990.001-t1.000.000 | 16 |
The tuples that do not appear in the tables containing the frequency of requests are never requested. They will remain inside the nodes that contain them before applying the EFA algorithm. The proposed EFA algorithm was applied for data described above. The chosen values for the algorithm parameters are written in Table 7.
Table 5. The frequency of requests of the tuples from the node N4.
| Tuples | Frequency |
| t100.001-t170.000 | 3 |
| t220.001-t330.000 | 7 |
| t450.001-t560.000 | 13 |
| t680.001-t770.000 | 8 |
Table 6. The frequency of requests of the tuples from the node N5.
| Tuples | Frequency |
| t200.001-t260.000 | 12 |
| t700.001-t830.000 | 6 |
| t920.001-t980.000 | 1 |
Table 7. The EFA algorithm parameters.
| Population size | Number of generation that did not improve the current solution | Probability of recombination | Probability of mutation |
| 200 | 50 | 0.7 | 0.1 |
After applying EFA algorithm, the way the tuples are redistributed to the nodes of the graph, by taking into account the frequency of the requests of the tuples, is described in Table 8.
An evolutionary algorithm called EFA was proposed for the redesign phase, meaning re-fragmentation and re-allocation, in our distributed system. The considered problem is a NP-Complete one. EFA was successfully applied and experimental results have proved the e.ciency of the proposed algorithm.
As future work, the method can be improved by computing the costs weighted with factors like local interest for fragments (recommend replication or not), realtime response importance (some applications do not need real-time response), data access frequency (balance sheet data may be consulted once in a month).
The weight of the factors in the cost computation can be changed in time, also changes in network topology or transmission media can influence the response time. The statistics are useful for rebalancing the system by re-computing the costs to obtain best response time for all queries on any site.
Table 8. Reallocation of tuples in nodes after applying EFA.
| Node | Dataset Fragmentation | Number of tuples/node |
| N1 | t680.000-t770.000, t1.000.001-t1.100.000 | 190.000 |
| N2 | t170.001-t200.000, t250.00-t260.000, t330.001-t380.000, t560.001-t610.000, t770.001-t830.000, t970.001-t980.000, t1.100.001-t1.200.000 | 310.000 |
| N3 | t1-t40.000, t90.000-t100.000, t260.001-t330.000, t380.001-t420.000, t880.000-t970.000, t990.001-t1.000.000 | 260.000 |
| N4 | t40.001-t90.000, t100.001-t170.000, t420.001-t560.000, t980.001-t990.000 | 270.000 |
| N5 | t200.001-t250.000, t610.001-t680.000, t830.001-t880.000 | 170.000 |
[1] Bäck, T., Fogel, D.B., Michalewicz, Z. (Editors), Handbook of Evolutionary Computation, Institute of Physics Publishing, Bristol and Oxford University Press, New York, 1997.
[2] Bäck, T., Optimal mutation rates in genetic search, Proceedings of the 5th International Conference On Genetic Algorithms, Ed. S. Forrest, Morgan Kaufmann, San Mateo, CA, 2-8, 1993.
[3] Dumitrescu, D., Lazzerini, B., Jain, L.C, Dumitrescu, A., Evolutionary Computation, CRC Press, Boca Raton, FL., 2000.
[4] Goldberg, D.E., Deb, K., A comparative analysis of selection schemes used in genetic algorithms, Foundations of Genetic Algorithms G.J.E. Rawlins (Ed.), Morgan Kaufmann, San Mateo, CA, 69-93, 1991.
[5] Moldovan, G., Reorganization of a Distributed Database, Babes-Bolyai University, Seminar of Models, Structures and Information Processing, Preprint nr. 5, p. 3-10, 1984.
[6] Levin, K. D., Morgan, H. L., Optimizing distributed databases-A framework for research, Proceedings of AFZPS NCC, vol. 44. AFIPS Press, pp. 473-478, 1975.
[7] Mitchell, M., An Introduction to Genetic Algorithms, MIT Press, Cambridge, MA, 1996.
[8] Oszu, M. T., Valduriez, P., Principles of Distributed Database Systems, Prentice Hall, Englewood Cli.s, NJ, 1999.
[9] Piattini, M. and Diaz, O., Advanced Database Technology and Design, Artech House, Inc. 685 Canton Street Norwood, MA 02062, 2000.
[10] Weiss, G., Multiagent System, A Modern Approach to Distributed Arti.cial Intelligence, MIT Press , USA, 2000.