
|
Некоторые современные методы решения оптимизационных задач Е.Н.Зайцева† , Ю.А.Станкевич‡ |
† Белорусский государственный университет информатики и радиоэлектроник, 220600 г. Минск, ул. П.Бровки, 6.
‡ Белорусский государственный экономический университет, кафедра информационных технологий, 220672 г. Минск, Партизанский пр.,26
Аннотация. В работе рассматриваются три нетрадиционных метода решения оптимизационных задач: генетические и самоорганизующиеся алгоритмы, а так же нечеткая логика. Показаны особенности их практического использования.
Ключевые слова: генетические алгоритмы, самоорганизующиеся принципы и алгоритмы, нечеткая логика, оптимизационные задачи.
Введение
Большое число прикладных задач из различных областей знаний сводится к оптимальным задачам. К настоящему времени накоплен огромный опыт решения оптимизационных задач, как для конкретных приложений [1-2], так и в обобщенном виде [3-4]. Все существующие методы решения можно разделить на: (a) детерминированные; (б) эвристические; (в) комбинированные.
Детерминированные методы дают точную оценку исследуемому процессу и однозначно определить функциональные связи между “входами” и “выходами”. Если такая связь является вероятностной, то мы имеем дело с детерминистическими вероятностными методами. Противоположными детерминистическим методам являются эвристические, в частности методы самоорганизации. В работе [5] А.Г. Ивахненко охарактеризовал их как методы абсолютно исследующие функциональные и вероятностные взаимосвязи “входов” и “выходов” некоторой системы. Они используют генераторы случайных комбинаций (гипотез) и интегральные самоотборы лучших из них по эвристическим критериям. Подход самоорганизации является общим, интегральным и не требует глубокого исследования каждого элемента системы в отдельности.
Полученные в последнее время методы решения оптимизационных задач преимущественно относятся к первым двум направлениям. Однако, например, для управления конъюнктурой рынка требуется иной подход. Здесь точные математические методы подчас остаются бессильными. Детермистическое направление эффективно при решении действительно небольших, специфических задач. и непригодно для решения трудноформаизуемых и сложных многоуровневых задач. К таким задачам относится, например, те в которых нельзя все исходные данные задать в числовом виде или вообще их получить (задачи психологии, социологии, экономики и т.д.). Проблема многомерности заключается в том, что даже в тех случаях, когда ввод и переработку данных удается формализовать в виде, пригодном для автоматической обработки, вычисленные затраты могут быть несоизмеримо велики. Например, такие ситуации возможны при решении задач экстремального управления [2, 5-6], экономического прогнозирования[7-8], задачи оценки надежности [9] и т.д.
Таким образом существует класс задач (экономических и технических) для которых детерминистические методы решения не приемлемы или не обеспечивают необходимой точности результатов.
Следовательно, альтернативный метод состоит в использовании эвристических методов: самоорганизующихся и генетических алгоритмов. Первые в свое время были исследованы в работах А.Г. Ивахненко и его научной школы [5-6, 8]. Генетические алгоритмы в каком-то смысле являются аналогом самоорганизующихся (впервые они были выведены Холландом [10]). В настоящее время они исследуются более интенсивно и находят свое приложение в обработке изображений, системах управления принятия решений [11-13]. Различие генетических и самоорганизующихся алгоритмов состоит в определении исходных данных и интерполяции процедуры самоорганизации. Известны примеры самоорганизующихся алгоритмов в системах управления [6].
Еще одним из современных методов решения оптимизационных задач является аппарат нечеткой логики. Это направление сочетает свойства детерминированного и детерминистического вероятностного подходов.
Понятие нечетких множеств и логики были впервые выведены Л. Заде [14]. В настоящее время в этом направлении ведутся интенсивные исследования [15-17]. Результат нечеткой логики очень широко используются при решении самых разнообразных прикладных задач (экономических, технических, медицинских и т.д.) [16-17].
Авторы настоящей работы ставят своей задачей выполнить обзор современных методов решения оптимизационных задач, которые уже получили достаточно широкую апробацию за рубежом. Это в первую очередь, генетические алгоритмы, алгоритмы с использованием методов самоорганизации и нечеткая логика. Это связано с тем, что в частности алгоритмы с использованием принципов самоорганизации в основном применялись для моделирования. Известные генетические алгоритмы носят преимущественно прикладной характер. Нечеткая логика наиболее часто используется в задачах принятия решений. В работе на элементарных примерах показана принципиальная возможность использования указанных подходов при решении оптимизационных задач.
1. Генетические алгоритмы
Генетические алгоритмы используются, при управлении различными процессами в современном логическом проектировании дискретных устройств и систем принятия решений
Они помогают решить целый класс комплексных задач, включающих комбинаторную оптимизацию и реализацию высокоточных инженерно-технических задач.
Суть этих алгоритмов заключается в имитации эволюционного процесса и большинство понятий и терминов заимствовано из генетики [10-12].
Генетические алгоритмы - это оптимизационные алгоритмы, относящиеся к классу вероятностных. Они сочетают элементы стохастических и детерминиских подходов. В связи с этим генетические алгоритмы нельзя отнести только к алгоритмам случайного поиска. Поиск решения осуществляется путем одновременного анализа нескольких ветвей эволюции. Причем, при эволюции “выживают” только наилучшие варианты решений, в то время как “плохие” решения “вымирают”. Для определения значимости каждого решения используется целевая (эволюционная) функция, которая выполняет роль окружающей среды при моделировании эволюционного процесса.
В начале генетического алгоритма формируется множество потенциальных решений (гипотез), которое представляет собой начальную популяцию. В большинстве случаев это множество формируется случайно. Однако, для увеличения скорости сходимости алгоритма в начальную популяцию, могут включаться решения, полученные с помощью другого оптимизационного метода. Размер начальной популяции определяется экспериментально, однако число потенциальных решений должно превышать одно.
Одним из наиболее важных элементов генетические алгоритмы являются кодированием потенциальных решений, т.е. формированием хромосомы. Полученная структура называется хромосомой. Хромосома состоит из более чем одного элемента (гена). Гены могут принимать бинарные, целочисленные и вещественные значения. Если обозначить ген как ij, то S-я хромосома определяется последовательностью VS = {i1, i2, i3, ... im}. Известны три основные вида хромосом:
Для строчных хромосом характерно, что изменение одного из генов не влечет за собой изменения остальных. В векторном описании хромосом существует взаимосвязь как минимум двух ген. Табличное представление хромосом характерно для решения транспортных задач с линейным и нелинейным ограничением переменных. Например, для задач целочисленного программирования генами являются значения переменных оптимизируемой системы.

После формирования начальной популяции, осуществляется процесс синтеза новых решений (поколений) задачи. Исходными данными для него являются хромосомы текущей популяции. Исследуемая в некоторый момент времени популяция называется текущей. В начале работы алгоритма текущая популяция совпадает с начальной. Новое поколение хромосом генерируется посредствам двух основных операций: скрещивания и мутации.
Скрещивание моделирует передачу наследственности хромосомами. Эта операция обуславливает целенаправленное закономерное “приближение” свойств хромосом к оптимальному решению.
Пусть эта процедура состоит в обмене элементов (генов) двух случайно выбранных хромосом. Такие хромосомы называются потомками. Потомки - результат преобразования - сочетают в себе свойства родителей. Например, скрещивание может быть реализовано как обмен генами с одинаковыми порядковыми номерами (рис.1).
Однако, при определении операции скрещивания имеет смысл учитывать особенности и специфику конкретной задачи. Число пар хромосом подвергающихся скрещиванию определяется коэффициентом скрещивания, на основе экспериментальных исследований

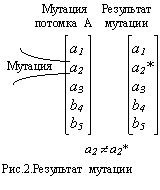
Мутация представляет собой случайное направленное одного или несколько ген (рис.2). Эта процедура позволяет избежать локального экстремума (решения близкому к оптимальному, но не оптимального). Выбор мутирующих генов в основном осуществляется случайным образом. Однако с учетом особенностей решаемой задачи можно предусмотреть приоритетную мутацию одних элементов хромосом по сравнению с другими для ускорения процедуры поиска глобального экстремума. Число хромосом, подвергающихся мутации определяется коэффициентом мутации. Коэффициент мутации показывает какой процент хромосом будет участвовать в этой операции и определяется экспериментально. Мутации могут подвергаться только потомки или потомки и родители совместно. Причем вероятность их мутации может быть различной.
После скрещивания и мутации размер популяции увеличивается (рис.3.). Однако для последующих преобразований необходимо сократить число хромосом текущей популяции. Такая процедура носит название селекции. В текущей популяции, состоящей из родителей и потомков либо только из потомков, производится отбор лучших решений, т.е. хромосом с наибольшим значением fittnes-функции. Эта функция показывает насколько исследуемая хромосома близка к оптимальному решению.
Для текущей популяции повторяются все описанные процедуры. Процесс продолжается до тех пор пока не будет получено оптимальное решение или заданное число поколений. При этом каждая последующая популяция должна быть лучше чем предыдущая. Решению задачи соответствует хромосома с максимальным значением fitness-function.
Таким образом для генетического алгоритма выделяется три основных этапа (рис.4.):
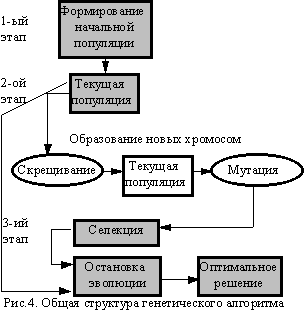
При разработке генетического алгоритма для конкретной задачи первоначально необходимо определить следующие компоненты:
Затем на основе тестовых данных в ходе экспериментальных исследований, определяются такие компоненты генетического алгоритма как (а) размер популяции; (б) скорость скрещивания; (в) скорость мутации.
Известно несколько основных типов генетических алгоритмов, в зависимости от определения операций скрещивания, мутации и селекции [10-13, 18]. Однако наибольший эффект при использовании генетических алгоритмов достигается в том случае, когда при определении этих компонент учитываются особенности решаемой задачи.
2. Использование методов самоорганизации в оптимизационных задачах
Интересные результаты для оптимизации получены с помощью. самоорганизующихся алгоритмов [5-6]. На основе этих алгоритмов моделировали сложные технические системы. Однако, как показано ими в работах [5, 8] принципы самоорганизации могут быть использованы и в оптимизационных задачах. Рассмотрим основные моменты теории самоорганизующихся алгоритмов. В преобладающем большинстве сложные математические модели не дают точного решения задачи. Это связано, во-первых, с тем что при моделировании необходимо учитывать ряд противоречивых параметров. Во-вторых, большое число учитываемых параметров сильно усложняет математическую модель, которая в пределе вообще не может быть решена имеющимися техническими средствами. Высокая точность моделирования всегда соответствует высокой сложности описания, не достижимой при детерминизме.
Методы самоорганизации, как антипод детерминистических методов, оперирует с такими общими категориями, как понятия элементарный алгоритм, эвристический критерий и интегральное воздействие. Рассмотрим эти понятия на примерах. Пусть существует сложная система в виде динамической сети взаимосвязанных элементов, похожих друг на друга.
Например, эвристический алгоритм - алгоритм действия элемента сложной динамической сети. Это закон действия фирмы или предприятия в экономической системе, закон образования значения входного сигнала (датчика) или некоторой промежуточной переменной.
Эвристический критерий - это критерий порогового самоотбора полезной информации, основанный на опыте решения аналогичных задач, направленный на достижение требуемых для человека результатов.
Интегральное воздействие можно определить как такое, которое не использует информации о состоянии каждого элемента сложной системы в отдельности, а выбирается по суммарному результату действия на множество элементов. Это, например, действие подоходного налога на некоторых производителей, действие пороговых элементов на множество входных сигналов.
Пожалуй, именно подоходный налог, нелинейная закономерность которого давно уже использовалась для управления стихией рынка, является наиболее типичным примером того, что называется “интегральным воздействием”. Простейшая нелинейность - пороговое действие налога, при котором фирмы с малым доходом вообще не облагаются, а со слишком большим - ликвидируются. Если нелинейность велика, подоходный налог становиться интегральным воздействием порогового типа: ничего от бедных и все от богатых. Простейшей реализацией интегральных воздействий в кибернетике (например, в перцептроне) служит пороговый элемент, пропускающий только часть входных сигналов ( элементарные алгоритмы которых достаточно хороши).
3. Нечеткая логика
В числе основных промышленных применений теории нечеткой логики можно указать экономическое управление, распознании образов и обработку изображений, принятие решений, анализ надежности и т.д. В настоящее время наметилась тенденция применения нечетких множеств в гуманитарных науках, лингвистике, психологии и в социологии. Вообще применение нечетких множеств более характерно для гуманитарных наук, т.к. там чаще приходится сталкиваться с нечеткими, субъективными данными. А теория нечетких множеств прежде всего ставит перед собой задачи непосредственного анализа и обработки именно таких неопределенных, неясных данных. В 1972г. Заде предложил теоретико-множественную интерпретацию лингвистических переменных и ограничений, которая отражала лингвистические аспекты отношения принадлежности в нечетких множествах.
Определение “нечеткого множества” чаще всего интерпретируют как величину МА(х), которая обозначает субъективную оценку степени принадлежности х множеству А, например МА(х) = 80%, означает, что х на 80% принадлежит А. Следовательно должны существовать “моя функция принадлежности”, “ваша функция принадлежности”, “еще чья-нибудь функция принадлежности” и т.д.
Несколько позже были сформулированы понятия нечеткой логики с лингвистическим, а нечисловым значением истинности. Согласно такой логике высказывание может принимать истинное значение типа: истинно, ложно, абсолютно истинно, совсем ложно и т.п. - каждое такое значение представляет собой нечеткое подмножество единичного интервала.
В том случае, когда речь идет о логике, то представляется некоторая четкая и жесткая система, которая позволяет все разделить на “Да” и “Нет” (истину и ложь). Это представление соответствует компьютерной логике или двузначной булевой алгебре. Однако в реальной действительности очень трудно все разделить на черное и белое. В работе [14, 19] Л.Заде двузначная оценка 0 или 1 расширена до неограниченной многозначной оценки выше 0 и ниже 1, т.е. впервые было введено понятие “нечеткое множество”. Теоретико-вероятностное понятие случайности уже давно отнесено к категории объективных понятий и рассматривается как дополнительное к понятию причинности; такое восприятие подкрепляется концепцией воспроизводимых элементов, которая согласуется с наблюдениями в области естественных наук и в технике. По-видимому. и к субъективной вероятности можно относиться как к шкале неоднозначности. Подобной объективной вероятности - самой популярной и неопределенной из концепций неопределенности - субъективная вероятность удовлетворяет аксиоме вероятностной меры и оказывается положительной и воспроизводимой. Однако широкое распространение разнообразия неясных, неопределенных и неточных явлений, событий и фактов, а также связей между объектами и операциями, показывает, что существуют различные класс неясности или неопределенности, которые не всегда будут связаны со случайностью или нечеткостью, как показано в табл. 1. Сейчас же только отметим, что для рассмотрения некоторых классов неопределенности и неясности могут оказаться полезными и эффективными такие совершенно различные подходы, как теория искусственного интеллекта и методы теории познания.
В повседневной жизни мы встречаемся с нечеткими выводами и нечеткими утверждениями, такими как, например: если в предприятие А вложено много средств, то оно принесет прибыль при том, предположении, что если в предприятие вложено много денег, то оно прибыльно.
Такого типа нечетки выводы Заде и имел в виду. Приближенное рассуждение может рассматриваться как обобщение правил модус поненс и модус толленс, соответствующих хорошо известным правилам модус поненс и модус толленс в исчислении условных высказываний. Для определения композиционного правила вывода Заде применил понятие нечеткого отношения. Следствия получаемые, исходя из композиционных правил Заде, не всегда совпадают с нашей интуицией. Причина рассогласования - в выборе операционного метода, который используется в нечетких отношениях. Согласно интуитивным представлениям отношений между A’ в посылке 2 и B’ в выводе (1) или между B’ в посылке 2 и A’ в выводе (2) должны быть такими, как показано в табл.2 (где х, y - имена объектов; А, А’, В и B’ - названия нечетких множеств, определенных на универсумах U, U, V и V составлено)
В табл. 3 указано, при каких композиционных правилах ввода удовлетворяются или не удовлетворяются каждое из отношений, перечисленных в табл.2.
Применение теории нечетких множеств экономике
Суть функционально стоимостного анализа (ФСА) состоит в системном технико-экономическом исследовании материальных и организационных структур в целях обеспечения эффективности их создания и функционирования из их действительного назначения.
Одной из наиболее сложных работ в ходе ФСА является выбор лучшего варианта исполнения функцией, который бы удовлетворял и потребителя и производителя. Большое разнообразие факторов учитываемых при этом часто вступают в противоречие друг с другом, что не позволяет точно отдать предпочтение одному варианту по сравнению с другим.
В связи с этим приходится прибегать к таким методам принятия решений, которые позволили бы получить наилучшее соотношение между конкурирующими показателями, в том числе качеством и затратами, т.е. прибегнуть к оптимизации.
В технических науках методы оптимизации, как правило, используются в процессе инженерного анализа, при этом применяются строго регламентированные технические величины.
Однако, с помощью только таких величин не удается решать многие задачи, возникающие, например, при создании нового продукта (учет влияния риска, неожиданный спад спроса на этот продукт, увеличение затрат на его производство к данному промежутку времени, эффективность и т.д.).
Стоимостные величины часто использующиеся в экономических науках (цена, себестоимость и т.д.), хотя и помогают в решении подобных задач, но зато и сами зависят от большого числа переменных, которые не всегда поддаются адекватной оценке, и поэтому снижают точность.
Исходя из всех перечисленных факторов трудность решения таких задач традиционными методами очевидна.
Критерии используемые для выбора решений на этапах ФСА, должны удовлетворять следующим основным требованиям: отражать сопоставление затрат и результатов, не противоречить критерию народнохозяйственной эффективности; иметь количественное выражение; быть пригодными для оценки различных технических решений на этапах проектирования; учитывать качественные различия сравниваемых вариантов; обеспечивать объективность оценки в условиях ограниченной исходной информации; и в тоже время быть относительно простыми. Одним из критериев такой оценки может быть показатель интегрального качества, представляющий собой функцию потребительской стоимости (полезности) и совокупных затрат.
Пусть К = {k1, k2, … , kp} - множество показателей качества, назовем его показателем интегрального (общего) качества.
Пусть Q = {q1, q2, … , qn} - множество потребительских стоимостей, назовем его потребительской полезностью.
Пусть С = {c1,c2, … , cm} - множество затрат на производство изделия , назовем его совокупные затраты, которые включают текущие суммарные производственные затраты + сопутствующие капитальные вложения в сфере эксплуатации + капитальные затраты в сфере проектирования и т.д.
Пусть ФR : Q? К® [1;0] есть функция принадлежности нечеткого бинарного отношения R. Для всех qI Q и всех кI К функция ФR(q, k) есть степень важности признака качества к по показателю оценки полезности q для потребителя. Отношение R можно представить в матричном виде.
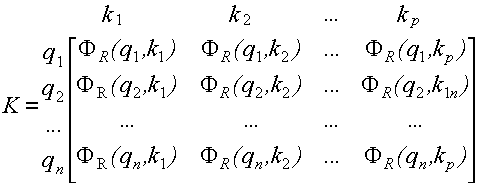
Пусть YS : K? C® [1;0] - есть функция отношения нечеткого бинарного отношения S. Для всех кI К и всех сI С функция YS(к, с) - степень (пропорциональности, принадлежности) совместимости с показателем качества. В матричной форме отношение имеет вид:

Теперь можно получить матрицу Т, элементы которой определяются функцией принадлежности ZT (q, c)=a ФR(q, k) / a YS(к, с)
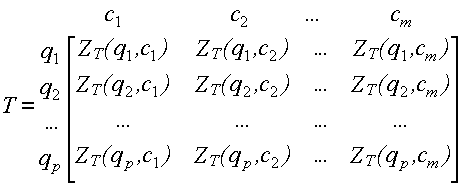
Функцию предпочтения ZT (qi, ci) можно интерпретировать как приближение к оптимальному соотношению полезности изделия и затратами, которыми оно достигается, она удовлетворяет определению выпуклого нечеткого подмножества (утверждение верно при определенных условиях выпуклости отношений R и S).
Понятно, что в данной модели порог оптимальности соотношения затрат и полезности может быть ограничен условием
![]()
Таким образом выбор лучшего варианта исполнения функцией ФСА, который бы удовлетворял и потребителей и производителей, описывается подмножеством
ZTi = {q/ZT(q, c)? l}.
Заключение
В работе рассмотрены нетрадиционные подходы к решению оптимизационных задач. Их объединяет идея устранения так называемого принципа несовместимости, который заключается в том, что с увеличением размеров и сложности системы существенно усложняется ее оптимизация с помощью известных детерминистических подходов. Другими словами при использовании формул существенно возрастает число переменных и параметров. Изменение отдельных переменных и определение параметров сильно затрудняется, и создание полностью адекватной модели, а тем более ее оптимизация становиться практически невозможной. Особенно актуальна эта задача при разработке и оптимизации экономических моделей в сфере бизнеса (помощь в принятии экономических решений, маркетинг, советы по вложению капитала, различного рода управление и планирование, помощь в подготовке контактов и т.д.).
Литература