An Effective Chromosome Representation for Evolving Flexible Job Shop Schedules

As the Flexible Job Shop Scheduling Problem (or FJSP) is strongly NP-hard, using an evolutionary approach to find near-optimal solutions requires effective chromosome representations as well as carefully designed parameters for crossover and mutation to achieve efficient search. This paper proposes a new chromosome representation and a design of related parameters to solve the FJSP efficiently. The results of applying the new chromosome representation for solving the 10 jobs x 10 machines FJSP are compared with three other chromosome representations. Empirical experiments show that the proposed chromosome representation obtains better results than the others in both quality and processing time required.

Flexible Job Shop Scheduling Problem, Genetic Algorithm, Chromosome Representation

1 Introduction

In today’s engineering domain, effective planning and scheduling has become a critical issue [1]. For instance, in manufacturing production lines, efficient and effective resource allocations are required to maintain sufficient inventories while maximizing production volume. Even on smaller problems, the number of possible plans and ways to allocate resources are prohibitively large to preclude any form of enumerative search. A commonly used abstraction of scheduling tasks is known as the Flexible Job Shop Problem (or FJSP). The FJSP is an extension of the classical job shop scheduling problem (or JSP) which allows an operation to be processed by any machine from a given set of resources. The task is to assign each operation to a machine and to order the operations on the machines, such that the maximal completion time (or makespan) of all operations is minimized.
This problem has wide applications in manufacturing and transportation systems [2][3]. Compared to the classical JSP, the FJSP is strongly NP-hard due to 1) assignment decisions of operations to a subset of machines and 2) sequencing decisions of operations on each machine. Therefore, heuristics based on randomized search have typically been the path taken to find good approximate solutions [4]. Recently, some researchers have focused on applying Genetic Algorithms (or GAs) to solve the FJSP and have obtained promising results [5][6][7]. In their works, chromosome representation is the first important task for a successful application of GA to solve the FJSP. Chen et al. [5] have used A-string (operations) and B-string (machines) representations, Mesghouni et al. [6] have used a parallel machine representation and a parallel job representation, while Kacem et al. [7] used an assignment table representation. In this paper, we propose a new chromosome representation that can be used by GAs to solve the FJSP efficiently.
This paper is organized as follows: Section 2 introduces the problem formulation. Sectio 3 describes three different chromosome representations described in literature and a new chromosome representation proposed by ourselves. Section 4 compares the results of the chromosome representation to three other chromosome representations described in Section 3 in solving the 10 jobs x 10 machines FJSP. Then, Section 5 and Section 6 represent crossover operators and mutation operators with suitable rates for the new chromosome representation. Finally, Section 7 summarizes and analyses the strengths and weaknesses of our representation.

2 Problem Formulation

The FJSP [5] can be defined as follows:

• There are n jobs, indexed by i, and these jobs are independent of each other.
• Each job i has li operations, and a set of precedence constraints P_i. The i-th job is denoted by J_i.
• Each job i is a set of operations O_i,j for j = 1, ..., l_i.
• There are m machines, indexed by k.
• For each operation O_i,j, there is a set of machines capable of performing it. The set is denoted by M_i,j, M_i,j
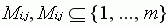
• The processing time of an operation O_i,j on machine k is predefined and denoted by t_ijk.
• Each operation cannot be interrupted during its performance (non-preemptive condition).
• Each machine can perform at most one operation at any time (resource constraint).
• The precedence constraints of the operations in a job can be defined for any pair of operations.
• The objective is to find a schedule with shortest makespan, where the makespan of a schedule is the time required for all jobs to be processed in the job shop according to the schedule.

3 Chromosome Representations

Solution Representation

Each chromosome in the population represents a solution of the problem. The solution is represented by an activity graph. The activity graph is a weighted directed acyclic graph G = (V, E, w). The node v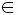V indicates the operation and the machine where the operation will be performed. E represents a set of edges in G. The weight w of the edge v_i v_j indicates the duration of the operation represented by the node vi. G can be transcribed to a Gantt chart to visualize its corresponding schedule. This section will briefly describe three chromosome representations commonly used for encoding GA-based solutions to the FJSP, after which, a new chromosome representation will be presented.

Chromosome A: Machine Order with Integers

This chromosome by Chen et al [5] consists of two integer strings (denoted as A1 and A2). The length of each string is equal to the total number of operations. String A1 assigns a machine index to each operation. The value of the j-th position of string A1 indicates the machine performing the j-th operation. String A2 encodes the order of operations on each machine. Both strings of Chromosome A are as follows:

• String A₁

where M_ijO is the machine to perform operation O_ij, M_O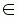ij M_ij.

• String A₂

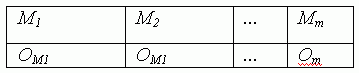
where O_Mk is an ordered set of operations on machine M_k.

Chromosome B: Machine Order with Bits

The chromosome by Paredis [8] also consists of two strings (denoted as B1 and B2). String B1 is identical to A1. String B1 is a bit string that gives the order of any pair of operations. A bit value of 0 indicates that the first operation in the paired-combination must be performed before the second operation. Both strings of Chromosome B are as follows:

• String B₁ (identical to A₁)

where M_ijO is the machine to perform operation O_ij, M_O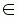ij M_ij.

• String B₂

where b_ijik is a bit specifying the precedence constraint between O_ij and O_ik.

Chromosome C: Simple Operation Order

Chromosome C by Ho and Tay [9] also consists of two strings (denoted as C1 and C2). This chromosome represents an instance of the FJSP, where the operations in each job have sequential precedence constraints. String C1 encodes the order of the operations with respect to other jobs. It does not specify the order of operations within the same job as this is already implied by its index value. String C2 represents the machine assignment to operations (as in A1 and B1) but with a twist. To ensure solution feasibility, the machine index is manipulated so that the string will always be valid. String C2 identifies those machines according to availability and viability. Therefore, if the machine is not available for an operation, it won’t have an index number in the set of machines and therefore this machine won’t be selected. Machine selection is indicated simple boolean values. Both strings of Chromosome C are given as follows:

• String C₁

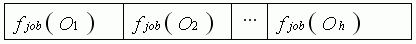
where O_h denotes the h_th operation to be performed, and f_job (O_h) indicates the job number of operation O_h.

• String C₂

Where M_Oij is the machine to perform operation O_ij, M_Oij 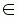M_ij, and f_idx (M_Oij) gives the set of index numbers of available machines for O_ij.

Fig. 1 gives an example of the FJSP for 2 jobs; each having 3 operations, running on 2 machines. One feasible solution for this problem is shown as an activity graph and a Gantt chart in Fig. 2. Note that the weight of an edge in the activity graph indicates the duration of the preceding operation node. The Chromosome C representation for this particular solution is shown in Fig. 3. Note that string C2 does not indicate the machine number but the index number of available machine. Therefore, machine 2 is the first available machine for O21.

Fig. 1. Example of a 2x2 FJSP

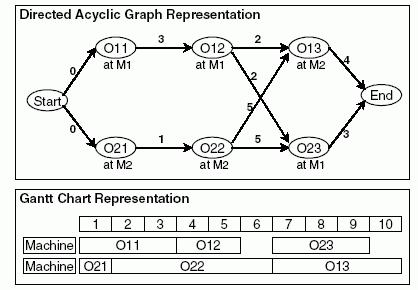
Fig. 2. Activity Graph and Gantt Chart for a Feasible Solution to the 2x2 FJSP

Fig. 3. Chromosome C Representation of the Feasible Solution to the 2x2 FJSP

Chromosome D: Operation Order with Bits

This chromosome is composed from chromosome representations B and C. The chromosome consists of three strings (denoted as D1, D2 and D3). D1 and D2 are equivalent to C1 and C2 respectively while D3 is similar to B2. String D3 is described as follows:

In string D₃, b_ijik is a bit specifying the precedence constraint between O_ij and O_ik. The constraints created by D₃ will only contain pairs of operations that are not included in the precedence constraints of the problem. Therefore, the possibility of invalid orders occurring due to precedence constraints is reduced. Also, a particular location in the chromosome only controls a specific property, therefore the difference between two solutions will be approximately proportional to the hamming distance between the chromosome representations. Table 1 shows the space complexity and the time complexity in converting each chromosome into a FJSP solution during each generation. T denotes the total number of job operations in the FJSP, c denotes the number of precedence constraints, and d denotes the length of the string D₃.

Although the asymptotic conversion complexity of Chromosome A is of the same order as Chromosome C, the former often has a larger hidden constant multiple. This is because, for each generation, Chromosome A has to be converted several times to process its partial string as follows: Though the validity of the machine can be checked in O(T) time, cycle detection in O(T + c) and cycle removal in O(c) time, other cycles often exists after the previous cycle is removed. Therefore, for one generation, the cycle detection and removal process maybe performed more than once.

4 Empirical Results

The purpose of this experiment is to empirically compare the four different chromosome representations. Our algorithm was coded in Java on a 2 GHz Pentium IV. The experiment was conducted for 100 runs of each chromosome representation to solve a randomized FJSP of 10 jobs x 10 machines using a population of 100 individuals.
Each run consists of at least 200 generations. Chromosome A, B and D may produce invalid solutions, therefore repairing the invalid chromosome can be optionally incorporated. Chromosome C [9] can only be used to solve the FJSP where the order of operations within a job is predetermined, therefore the problem definition for the chromosome C does not include randomized precedence constraints. The results of the experiment are shown in Table 2.

Table 2. Experimental results

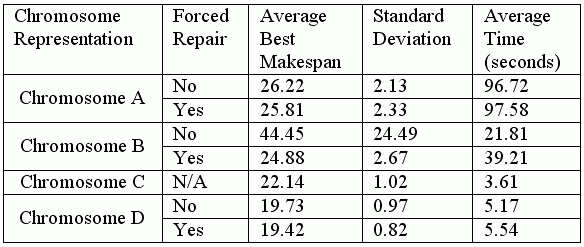
In terms of computation time, Chromosome A was the slowest. As strings A1 and A₂ of Chromosome A must be processed separately, the algorithm is not strictly a canonical GA. Each time A₁ was modified, A₂ had to be rebuilt [5]. As this process was performed for every generation, the total time required increased significantly. In contrast, the strings in B₁, C₁, and D1 can be modified independently of B₂, C₂, and D₂. The empirical results validate that these chromosomes are empirically faster. The fastest result was produced by chromosome C. Unfortunately, this representation was only able to solve the FJSP with ordered precedence constraints. Although the chromosome D was not the fastest, it could solve the general FJSP with acceptable computational time. As Chromosome A, B, and D may produce invalid representation, the forced mechanism to repair the invalid chromosome must be incorporated. For these chromosome representations, the presence of a repair mechanism always improves the makespan because it takes a larger number of generations to get a valid chromosome from the invalid chromosome by the using the standard crossover and mutation operator without any repair mechanism. From the result in Table 2, it can also be observed that the average best makespan produced by Chromosome B without a repair mechanism is very high. This indicates that Chromosome B would produce many invalid chromosomes. Without repair, the solution can only be found in 62 cases out of 100. The repair mechanism improves the solution of Chromosome B significantly. It could also be observed that the additional computation time for the repair mechanism of Chromosome B was also more significant than the other representations. In terms of the average best makespan, Chromosome D gives the best result compared to the other three representations. This is due to the simplicity of Chromosome D’s representation as compared to the others. Chromosome D also has a smaller standard deviation. Therefore, chromosome D is better in term of robustness and stability compared to the other chromosome representations used on this experiment.

5 Crossover Rates

Crossover Operators

String D₁ of Chromosome D describes the order of jobs. Therefore, offsprings may not be genetically reproduced by using standard 1-point or 2-point crossover, as the result may become unfeasible. We use order-preserving 1-point crossover operator [5] for D₁. The following is an example of order-preserving 1-point crossover given two strings D₁(1) and D₁(2).

Before crossover: a crossover b
String D1(1): 0 0 | 1 0 1 1
String D1(2): 1 0 | 1 0 0 1
After crossover:
String D1(3): 0 0 | 1 1 0 1
String D1(4): 1 0 | 0 0 1 1

String D₁(3) consists of partial strings denoted as D₁(3)a and D₁(3)b. String D₁(3)a, which contains the elements before the crossover point, is constructed from D₁(1)a. Therefore, D₁(3)a is “0 0” in this example. The string D₁(3)b, which contains elements after the crossover point, is constructed by removing the first occurrences of elements that are now in string D₁(3)a from the string D₁(2). In this case, the first two 0’s of string D₁(2) are removed, and therefore the string D₁(3)b is “1 1 0 1”. This method is also similarly applied to obtain D₁(4). It can be seen that the number of 0’s and 1’s are preserved by this method, and therefore the string D₁ of the offspring will always be valid. For string D₂ and D₃, we use the standard 1-point or 2-point crossover operator. For string D₂, the invalid machine index assignment is handled separately. If there exist invalid indices of available machines in string D₂ after crossover is applied, then the machine is reassigned randomly to a valid machine index number.

Suitable Rates for Crossover Operators

The canonical GA relies mainly on its operators to control the diversity of the population from one generation to the next. An experiment was conducted to study the effects of the crossover rate on the optimality of the makespan when using Chromosome D. In order to show the significance of the observed parameter and reducing the effects of the other factors, all other parameters are kept constant. Order-preserving 1- point crossover operator is used for the string D1, and standard 1-point crossover operator is used for the string D2 and D3, and the experiment is conducted without mutation. Therefore, the population will only be affected by the crossover operator. We use a modified JSP standard problem instance ft10 from Fisher and Thompson [10] with 10 machines, 10 jobs, each with 10 operations and vary the crossover rate from 0 to 1 with an interval step of 0.05. The experiment was repeated 100 times, and the averages of the best makespan were observed. The graphs of the average best makespans and its standard deviations are shown in Fig. 4. As the crossover rate increases, the average of the best makespans is observed to decrease gradually. The graph shows a significant improvement initially when the crossover rate is small. With a larger crossover rate, there is little improvement on the result and the trend flattens out. We conjecture that a crossover rate of greater than 0.85 may produce the best result. However, without mutation, it is unlikely to be the global optimal.

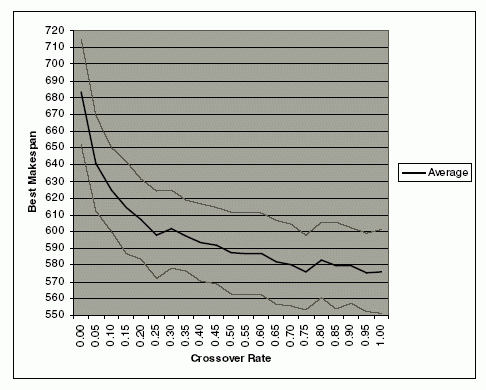
Fig. 4. Effects of crossover rate on the best makespan

6 Mutation Rates

Mutation Operators

Mutation can be applied to String D1 of Chromosome D by swapping two elements at two randomly selected locations. Another mutation operator that can be applied is the two-opt mutation operator [11]. This operator inverts the order of operations between two randomly selected locations. In this experiment, the string D1 is mutated by swapping two elements at two randomly selected locations, because this is commonly used for resource scheduling [12]. String D2 can be mutated by randomly changing the machine indices. The invalid machine assignment may be handled separately, or incorporated into the operator. By incorporating it into the operator, the mutation operator can be considered as a constraint- preserving operator that will always ensure feasibility of the mutated instance. Finally, string D3 is a sequence of bits, which can be mutated by simply inverting a random number of them.

Suitable Rates for Mutation Operators

This experiment uses the same configuration, as well as the same randomized problem as in the previous experiment on the crossover operator. In this experiment, the crossover operator was set at 0.95. The mutation rate was varied from 0 to 1. The experiment was repeated 100 times, and the averages of the best makespan were observed. The graphs of the average best makespans and its standard deviations are shown in Fig. 5 and Fig. 6. Fig. 5 shows that the best result is achieved when the mutation rate is around 0.025. There is a significant improvement on the average of makespan from mutation rate of 0 to 0.025. As the mutation rate increases beyond 0.025, the average of the best makespan also increases gradually. To investigate the significant improvement on the best makespan from mutation rate of 0 to 0.025, another experiment was conducted by varying the mutation rate from 0 to 0.03 with an interval of 0.001. The graph of the result is shown on Figure 6. In the interval of 0 to 0.004, the best makespan drops significantly. This shows the importance of the mutation operators in reducing the best makespan. As the mutation rate increases, the best makespan is quite stable and slowly increases beyond 0.018. The trend of increasing makespan after 0.03 is further supported by the trend of the best makespan after 0.025 in Fig. 6. A large mutation rate may destroy the good schemata and reduce the GA’s ability to find better makespans. Therefore, we conjecture that the mutation rate around 0.006 to 0.017 would produce the best result. The experiment was conducted using Chromosome D, with high crossover at null mutation until equilibrium is reached, then followed by regeneration and application of mutation at the previous equilibrium crossover point (or greater). We believe this is a good approach to solve the FJSP.

7 Conclusions

In this paper, a new chromosome representation for solving the FJSP was proposed. The three partial strings of Chromosome D are independent; therefore they can be modified separately by appropriate genetic operators. A particular location in the chromosome only controls a specific property, therefore the difference between two solutions will be proportional to the hamming distance between the chromosome representations. The order specified by String D₁ is always valid. The transitive closure of the precedence constraints has to be constructed to create String D₃. This may incur an overhead at the initial stage, but it will reduce the possibility of invalid orders due to precedence constraints as the explicit and implied precedence constraints of the problem are not included in the chromosome.

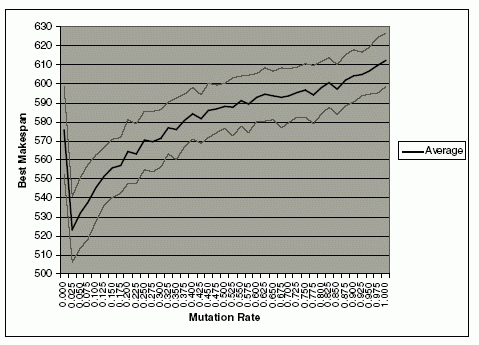
Fig. 5. Effects of mutation rate on the best makespan

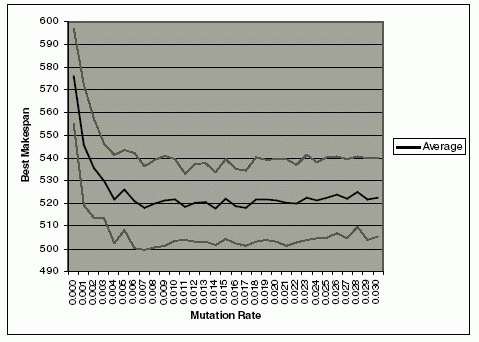
Fig. 6. Effects of mutation rate on the best makespan

The crossover operator and mutation operator for the new chromosome representation and their suitable rates were also presented. From the experiments conducted, it has been empirically shown that the new chromosome representation produces a schedule with shorter makespan. By using Chromosome D, with high crossover (> 0.85) at null mutation until equilibrium is reached, then followed by regeneration and application of mutation (around 0.006 to 0.017) at the previous equilibrium crossover point (or greater) would produce a lower average makespan.

References

1.Jain A.S. and Meeran S., “Deterministic Job-Shop Scheduling: Past, Present and Future”, In European Journal of Operation Research, 113 (2), 390-434, 1998.
2.Pinedo, M., Chao, X., Operations scheduling with applications in manufacturing and services, McGraw-Hill, Chapter 1, 2 – 11, 1999.
3.Gambardella, L. M., Mastrolilli, M., Rizzoli, A. E., Zaffalon, M., “An optimization methodology for intermodal terminal management”, In Journal of Intelligent Manufacturing, 12, 521-534, 2001.
4.Jansen K., Mastrolilli M., Solis-Oba R., "Approximation Algorithms for Flexible Job Shop Problems", In Proceedings of Latin American Theoretical Informatics (LATIN'2000), LNCS 1776, 68-77, 1999.
5.Chen, H., Ihlow, J., and Lehmann, C., “A genetic algorithm for flexible job-shop scheduling”, In Proceedings of IEEE International Conference on Robotics and Automation, 2, 1120 – 1125, 1999.
6.Mesghouni K., Hammadi S., Borne P., “Evolution programs for job-shop scheduling”, In Proc. IEEE International Conference on Computational Cybernetics and Simulation, 1, 720 -725., 1997.
7.Kacem I., Hammadi S. and Borne P., “Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems”, In IEEE Transactions on Systems, Man and Cybernetics, 32(1), 1-13, 2002.
8.Paredis, J., Exploiting constraints as background knowledge for genetic algorithms: A case-study for scheduling, Ever Science Publishers, The Netherlands, 1992.
9.Ho N. B. and Tay J. C., “GENACE: An Efficient Cultural Algorithm for Solving the Flexible Job-Shop Problem”, accepted for publication in IEEE Congress of Evolutionar Computation 2004.
10.Fisher, H., Thompson, G.L., “Probabilistic learning combinations of local job-shop scheduling rules”, Industrial Scheduling, Prentice Hall, Englewood Cliffs, New Jersey, 225-251,1963.
11.Lin, S., and Kernighan, B. W., “An effective heuristic for traveling salesman problem”, In Operations Research, 21, 498-516, 1973.
12.Syswerda, G., Schedule optimization using genetic algorithms, Ed. L Davis (New York: Van Nostrand Reinhold) 332-349, 1991.