Эффективное Представление Хромосомы для составления цехового гибкого расписания

Проблема составления гибкого цехового расписания работы (FJSP)- это NP-сложная задача, используемый эволюционный подход для нахождения субоптимальных решений требует эффективного представления хромосомы так же как тщательной проработки параметров для кроссинговера и мутациидля достижения эффективного поиска. Эта статья предлагает новое эффективное представление хромосомы и проект связанных параметров для эффективного решения задачи. Результаты применения нового представления хромосомы для решения задачи 10 работ x 10 машин FJSP - сравниваются с тремя другими представлениями хромосомы. Эмпирические эксперименты показывают, что предложенное представление хромосомы получает лучшие результаты чем другие и в качестве и в требуемой продолжительности обработки. Проблема составления гибкого цехового расписания, Генетический алгоритм, Хромосома

Проблема составления гибкого цехового расписания, Генетический алгоритм, Хромосома

1 Введение

В сегодняшней технической области, эффективное планирование и расписание работы стало критической проблемой [1]. Например, в линиях серийного производства, для выгодного и эффективного распределене ресурса обязаны поддерживать достаточные материальные запасы, максимизируя объем производства. Даже на меньших проблемах, число возможных планов и способов распределения ресурсов является предельно большим, чтобы устранить любую форму исчисляющего поиска. Обычно используемая абстракция планирования, задач известна как Гибкая Проблема Цехового расписания (или FJSP). FJSP - расширение классического цехового расписания (или JSP), которая позволяет операции быть обработанной любой машиной от данного набора ресурсов. Задача состоит в том, чтобы назначить каждую операцию на машину и заказывать операции на машинах, такой, что максимальное время завершения (или makespan) всех операций минимизировано.
Эта проблема имеет широкие заявления в системах производства и транспортировки [2] [3]. По сравнению с классическим JSP, FJSP это строго NP- сложная задача из-за 1) решений назначения операций к подмножеству машин и 2) установление последовательности операций на каждой машине. Поэтому, эвристика, основанная на случайном поиске типично была путем, принятой, для нахождения хороших приблизительных решений [4]. Недавно, некоторые исследователи сосредоточились на том, чтобы применять Генетические Алгоритмы (или ГА), чтобы решить FJSP и получили многообещающие результаты [5] [6] [7]. В их работах, представление хромосомы - первая важная задача для успешного заявления GA, которая решит FJSP. Chen и др. [5] использовали A-строку (операции) и B-строку (машины) представления, Mesghouni и др. [6] использовали параллельное представление машины и параллельное представление работы, в то время как Kacem и др. [7] использовал представление стола назначения. В этой бумаге, мы предлагаем новое представление хромосомы, которое может использоваться ГА, чтобы решить FJSP эффективно.
Эта бумага организована следующим образом: Секция 2 вводит формулировку проблемы. Секция 3 описывает три различных представления хромосомы, описанные в литературе и новом представлении хромосомы, предложенном нами непосредственно. Секция 4 сравнивает результаты представления хромосомы с тремя другими представлениями хромосомы, описанным в Секции 3 в решении этих 10 работ x 10 машин FJSP. Секция 5 и Секция 6 представляют операторы кроссинговера и операторы мутации с подходящими нормами для нового представления хромосомы. Наконец, Секция 7 суммирует и анализирует сильные стороны и слабости нашего представления.

2 Постановка задачи

FJSP [5] может быть описана следующим образом:

• Существует n работ, с индексом i, эти работы не зависят друг от друга.
• Каждая работа i имеет li операций, и множество принудительных ограничений P_i. i-я работа обозначена J_i.
• Каждая работа i есть множество операций O_i,j для j = 1, ..., l_i.
• Задано m машин, с индексами k.
• Для каждой операции O_i,j, существует множество машин способных сделать ее. Это множество обозначим M_i,j, M_i,j
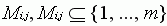
• Время обработки каждой операции O_i,j на машине k известен и имеет величину t_ijk.
• Каждая операция не может быть прервана до ее завершенияя.
• Каждая машина в каждый момент времени может выполнять только 1 операцию.
• Ограничения предшествования операций в работе могут быть определены для любой пары операций.
• Цель состоит в том, чтобы найти последовательность с самым коротким временем завршения, где короткое время завршения - время, требуемое для всех рабочих мест чтобы обработать все операции согласно расписанию.

Для простоты используем матрицу для обозначения M_ij и t_ijk.

3 Представление хромосомы

Представление решения

Каждая хромосома есть решение задачи.Решение можно представить в виде графа. Граф представляет собой утяжеленный направленный нецикличный граф G = (V, E, w). Вершина v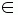V определяет операции и машину, где будет реализована данная операция. E представляет собой множество граней в G. Вес w грани v_i v_j обозначает длительность операции представленной гранью vi. G может быть перезаписана в Grantt симол для визуализации соответствующего расписания. Эта секция кратко опишет три представления хромосомы, обычно используемые для того, чтобы кодировать решения ГА FJSP, после которого, новое представление хромосомы будет представлено.

Хромосома A: Целочисленный порядок машино

Эта хромосома Chen и другие [5] состоит из двух строк целого числа (обозначенный как A1 и A2). Длина каждой строки равна общему количеству операций. Строка A1 назначает индекс машины на каждую операцию. Ценность j-го положения строки A1 указывает машину, выполняющую j-ю операцию. Строка A2 кодирует порядок операций на каждой машине. Обе строки Хромосомы A следующие:

• Строка A₁

где M_ijOмашина, чтобы выполнить операцию O_ij, M_O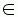ij M_ij.

• Строка A₂

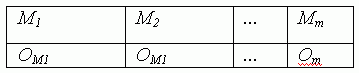
где O_Mk набор порядка операций на машине M_k.

Хромосома B: Битовый порядок маши

Хромосома Paredis [8] также состоит из двух строк (обозначенный как B1 и B2). Строка B1 идентична A1. Строка B1 - битовая строка, которая задает порядок любой пары операций. Битовое значени 0 указывает, что первая операция в комбинации должна быть выполнена перед второй операцией. Обе строки Хромосомы B следующие:

• СтрокаB₁ (идентична A₁)

где M_ijO машина, чтобы выполнить операцию O_ij, M_O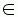ij M_ij.

• Строка B₂

где b_ijik бит определяет предшествующее ограничение между O_ij и O_ik.

Хромосома C: Простая последовательность операций

Хромосома C Ho и Теем [9] также состоит из двух строк (обозначенный как C1 и C2). Эта хромосома представляет случай FJSP, где операции в каждой работе имеют последовательные ограничения предшествования. Строка C1 кодирует заказ операций i, с учетом других рабочих мест. Это не определяет последовательность операций в пределах той же самой работы, поскольку это уже подразумевается ее ценностью индекса. Строка C2 представляет назначение машины на операции (как в A1 и B1), но с завихрением. Чтобы гарантировать выполнимость решения, индексом машины управляют так, чтобы строка всегда правомерной. Строка C2 идентифицирует машины согласно их пригодности и жизнеспособности. Поэтому, если машина будет не доступна для операции, то это не будет иметь номера индекса в наборе машин, и поэтому эта машина не будет отобрана. Выбор машины обозначен простыми булевыми значениями. Обе строки Хромосомы C даются следующим образом:

• Строка C₁

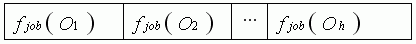
где O_h обозначает h_th выполненные операции , и f_job (O_h) показывающие номера работ в операции O_h.

• Строка C₂

Где M_Oij машина выполняющая операцию O_ij, M_Oij 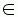M_ij, и f_idx (M_Oij) дает множество номеров индексов доступных машин для O_ij.

Фиг.1 показывает пример FJSP для 2-х работ; каждая имеет 3 операции выполняемых на 2-х машинах. Одно подходящее решение этой проблемы показано как активыный граф и диаграмма Ганта в фиг.2. Нужно заметить, что вес грани графа показывает направление предшествующего операционного узла. Представление Хромосомы С для данного решения показано в Фиг.3. Нужно заметить, что строка С2 не показывает номера машин, а показывает индексы номеров доступных машин. Поэтому машина 2 - первая доступная машина для O21

Фиг. 1. Пример 2x2 FJSP

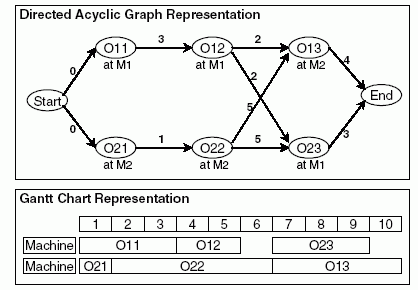
Фиг. 2.Граф работы и диаграмма Gantt для Выполнимого Решения 2x2 FJSP

Фиг. 3. Хромосома C Представление подходящего решения для 2x2 FJSP

Хромосома D: Битовый порядок операций

Эта хромосома составлена из представлений хромосомы B и C. Хромосома состоит из трех строк (обозначенный как D1, D2 и D3). D1 и D2 эквивалентны C1 и C2 соответственно, в то время как D3 подобен B2. Строка D3 описана следующим образом:

В строке D₃, b_ijik бит определяющий старшинство ограничений между O_ij и O_ik. Ограничения созданные в D₃ содержат лишь пары операций, которые не включены в предыдущие ограничения задачи. Поэтому, возможность недействительных заказов, происходящих из-за ограничений предшествования уменьшена. Кроме того, специфическое местоположение в хромосоме только управляет определенными параметрами, поэтому различие между двумя решениями будет приблизительно пропорционально расстоянию между представлениями хромосомы. Таблица 1 показывает комплексность и временую задержку в преобразовании каждой хромосомы в решение FJSP в течение каждого поколения. T обозначает общее количество операций работы в FJSP, c - обозначает число ограничений предшествования, и d обозначает длину строки D₃.

Хотя асимптотическая конверсионная сложность Хромосомы A имеет тот же самый порядок что и Хромосома C, первая часто имеет большее скрытое постоянное кратное число. Это - потому что, для каждого поколения, Хромосома A должна быть преобразована несколько раз, чтобы обработать ее частичную строку следующим образом: Хотя достоверность машины может быть зарегистрирована O (T) время, обнаружение цикла в O (T + c) и удалении цикла в O (c) времени, другие циклы часто существуют после того, как предыдущий цикл удален. Поэтому, для одного поколения, обнаружение цикла и удаление обрабатывают возможно выполненный не раз.

4 Эмпирические результаты

Цель этого эксперимента состоит в том, чтобы опытным путем сравнить четыре различных представления хромосомы. Наш алгоритм был закодирован в Яве на 2 ГГц Pentium IV. Эксперимент проводился для 100 пробегов каждого представления хромосомы, чтобы решить случайный FJSP 10 работ x 10 машин, используя популяцию в 100 особей. Каждый пробег состоит по крайней мере из 200 поколений.
Хромосома A, B и D может произвести неудовлетворительные решения, поэтому восстанавление недействительной хромосомы может быть включено произвольно. Хромосома C [9] может только использоваться, чтобы решить FJSP, где заказ операций в пределах работы определен, поэтому определение проблемы для хромосомы C не включает случайных ограничения предшествования. Результаты эксперимента показаны в Таблице 2.

Таблица 2. Результаты эксперимента

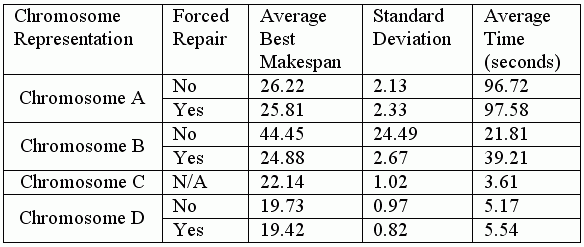
В терминах времени вычисления, Хромосома A была самая медленная. Так как строки A₁ и A₂ Хромосомы А должны быть обработанным отдельно, алгоритм не строго канонический ГА. Каждый раз, когда A₁ был изменен, A₂ должен был быть восстановлен [5]. Поскольку этот процесс был выполнен для каждого поколения, полное время работы значительно увеличелось. Напротив, строки в B₁, C₁, и D₁ могут быть изменены независимо от B₂, C₂, и D₂. Эмпирические результаты подтверждают что, эти хромосомы эмпирически быстрее. Самый быстрый результат был произведен хромосомой C. К сожалению, это представление было только в состоянии решить FJSP с заказанными ограничениями предшествования. Хотя хромосома D не была самая быстрая, она могла решить общую FJSP с приемлемым вычислительным временем. Так как Хромосома A, B, и D может произвести неудовлетворительное представление, принудительный механизм, чтобы восстановить неудовлетворительное хромосому должен быть включен. Для этих представлений хромосомы, присутствие механизма ремонта всегда улучшает максимальное время завершения, потому что требуется большее число поколений, чтобы получить действительную хромосому от неудовлетворительной хромосомы использованием стандартного кроссинговера и оператора мутации без любого механизма восстановления. Из результата Таблице 2, можно наблюдать, что среднее число лучше максимальное время завершения полученое Хромосомой B без механизма ремонта очень высоко. Это указывает, что Хромосома B произвела бы много недействительных хромосом. Без ремонта, решение может только быть найдено в 62 случаях из 100. Механизм ремонта значительно улучшает решение Хромосомы B. Можно также заметить, что дополнительное время вычисления для механизма ремонта Хромосомы B было также более существенно чем в другх представления. В терминах среднего числа лучшее максимальное время завершения, дает Хромосома D. Это происходит из-за простоты представление Хромосомы по сравнению с другими. Хромосома D также имеет меньшее стандартное отклонение. Поэтому, хромосома D лучше в сроке надежности и стабильности по сравнению с другими представлениями хромосомы, используемыми на этом эксперименте.

5 Оценка оператора кроссинговера

Оператор кроссинговера

Строки D₁ Хромосомы D, описывает порядок работ. Поэтому, потомки не могут быть генетически воспроизведены при использовании стандартного 1 и 2-х точечных операторов, поскольку результат мог стать неосуществимым. Мы используем сохраняющий 1-точечный оператор кроссинговера [5] для D₁. Следующее - пример сохраняющий 1-точечный оператор кроссинговера [5] для D₁(1) и D₁(2).

До кроссинговера: бит кроссинговера
Строка D1(1): 0 0 | 1 0 1 1
Строка D1(2): 1 0 | 1 0 0 1
После кроссинговера:
Строка D1(3): 0 0 | 1 1 0 1
Строка D1(4): 1 0 | 0 0 1 1

Строка D₁(3), состоит из частичных строк, обозначенных как D₁(3)a и D₁(3)b. Строки D₁(3)a, которая содержит элементы перед оператором кроссинговера, построена из D₁(1)a. Поэтому, D₁(3)a в этом примере "0 0" . Строка D₁(3)b, содержащая элементы после кроссинговера, построена, путем удаления первых возникших элементов, которые находятся теперь в строке D₁(3) от строки D₁(2). В этом случае, первые два 0 строки, D₁(2) удалены, и поэтому строка D₁(3)b, - "1 1 0 1". Этот метод также применен, чтобы получить D₁(4). Можно заметить, что число 0 и 1 сохранено этим методом, и поэтому вереница, D1 потомства всегда будет действительна. Для строки D₂ и D₃, мы используем стандартный 1-но и 2-х точечный оператор кроссинговера. Для строки D2, недействительное назначение индекса машины обработано отдельно. Если там существуют недействительные индексы доступных машин в веренице D₂ после того, применения кроссинговера, то машина повторно случайно назначена на действительное число индекса машины.

Подходящие нормы для оператора кроссинговера

Канонический GA полагается главным образом на его операторы, чтобы управлять разнообразием популяции от одного поколения к следующему. Эксперимент проводился, чтобы изучить эффекты оператора кроссинговера на оптимизацию максимального времени решения, используя Хромосому D. Чтобы показывать значение наблюдаемого параметра и сокращения эффектов других факторов, все другие параметры сохранены постоянными. Сохраненый 1-точечного оператора кроссинговера используются для строки D1, и 1-точечный оператора кроссинговера, используется для строк D2 и D3, и эксперимент проводится без мутации. Поэтому, население будет затронуто только оператором кроссинговера. Мы используем измененный стандартный случай проблемы JSP ft10 от Fisher и Thompson [10] с 10 машинами, 10 работами, каждый с 10 операциями и изменяем вероятность кроссинговера от 0 до 1 с шагом 0.05. Эксперимент был повторен 100 раз, и средние числа лучшего времени решения были соблюдены. График среднего числа лучшего времени решения и его стандартных отклонений показывают в рис. 4. Так как вероятность кроссинговера увелчивалось, среднее число лучшего решения, уменьшается постепенно. График показывает существенное усовершенствование первоначальноого решения, когда вероятность кроссинговера является маленькой. С большей вероятность кроссинговера, есть небольшое усовершенствование на результате, и тенденция выравнивается. Мы догадываемся, что вероятность кроссинговера больше чем 0.85 может произвести лучший результат. Однако, без мутации, это вряд ли будет глобальное оптимальное решение.

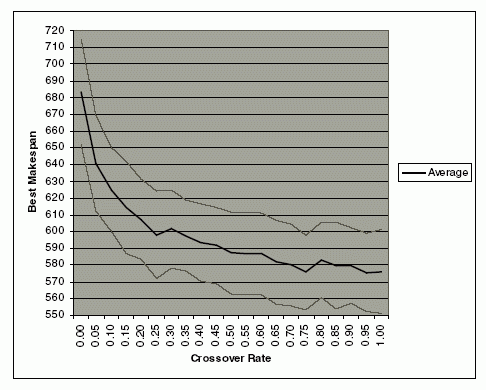
Рис. 4. Влияние вероятности кроссинговера на время решения

6 Размеры оператора мутации

Операция мутации

Мутация может быть применена для строк D1 Хромосомы D, путем обмена двух элементов в двух слачайно отобранных позициях. Другой оператор мутации, который может быть применен - двойной оператор мутации [11]. Этот оператор инвертирует порядок операций между двумя случайно отобранными позициями. В этом эксперименте, строка D1 видоизменена, путем обмена элементов в двух случайно отобранными позициях, потому что это обычно используется как способ составления расписания [12]. Строка D2 может быть видоизменена, путем случайного изменяя индексов машин. Недействительное назначение машины может быть обработано отдельно, или включено в оператор. Включая это в оператор, оператор мутации можно рассмотреть как ограничение - сохраняющий оператор, который будет всегда гарантировать выполнимость видоизмененного случая. Наконец, вереница, D3 является последовательностью битов, которые могут быть видоизменены, просто инвертируя их число случайное.

Наилучший интервал вероятности мутации

Этот эксперимент использует ту же самую конфигурацию, так же как ту же самую случайную проблему как в предыдущем эксперименте над оператором кроссинговера. В этом эксперименте, оператор кроссинговера был установлен с вероятностью 0.95. Норма мутации была различна от 0 до 1. Эксперимент был повторен 100 раз, и средние числа лучшего времени решения были соблюдены. Графы среднего числа лучше всего времени решения и его стандартных отклонений показывают рис. 5 и рис. 6. Рис. 5 показывает, что лучший результат достигнут, когда норма мутации - приблизительно 0.025. Есть существенное усовершенствование в среднем времени решения от нормы мутации 0 к 0.025. Как увеличения нормы мутации вне 0.025, среднее число лучшего времени решения также увеличивается постепенно. Чтобы исследовать существенное усовершенствование на лучшем времени решени от нормы мутации 0 к 0.025, проводился другой эксперимент, изменяя норму мутации от 0 до 0.03 с интервалом 0.001. График результата показан на иллюстрации 6. В интервале 0 к 0.004, лучшее время решения понижается значительно. Это показывает важность операторов мутации в сокращении лучшего времени решения. Так как нормы мутации увеличивается, лучшее время решения весьма устойчиво и медленно увеличивается вне 0.018. Тенденция увеличения времени решения после 0.03 далее поддержана тенденцией лучшего времени решения после 0.025 в рис. 6. Большая норма мутации может разрушить хорошие схемы и уменьшить способность GA найти лучшее время решения. Поэтому, мы считаем, что норма мутации приблизительно 0.006 к 0.017 произвели бы лучший результат. Эксперимент проводился, используя Хромосому D, с высокой вероятностью оператора кроссинговера с нулевой мутацией, пока равновесие не будет достигнуто, затем сопровождаемый регенерацией и заявлением мутации в предыдущем пункте перехода равновесия (или большее). Мы полагаем, что это - хороший подход решить FJSP.

7 Заключение

В этой бумаге, было предложено новое представление хромосомы для решения FJSP. Три частичных строки Хромосомы D независимы; поэтому они могут быть изменены отдельно соответствующими генетическими операторами. Специфическое местоположение в хромосоме только управляет определенной собственностью, поэтому различие между двумя решениями будет пропорционально расстоянию между представлениями хромосомы. Порядок, определенный строки D₁ всегда действителен. Переходное закрытие ограничений предшествования должно быть построено, чтобы создать строку D₃. Это может привести к переполнению в начальной стадии, но это уменьшит возможность недействительных заказов из-за ограничений предшествования, поскольку явные подразумеваемые ограничения предшествования проблемы не включены в хромосому.

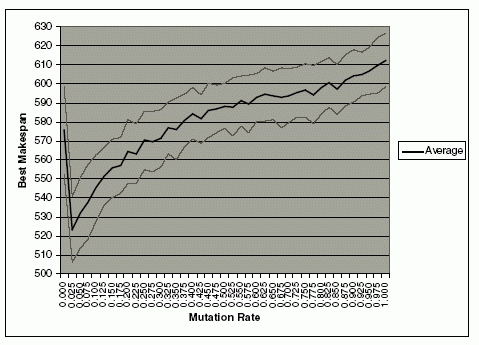
Рис. 5. Влияние мутаци на велечину времени решения

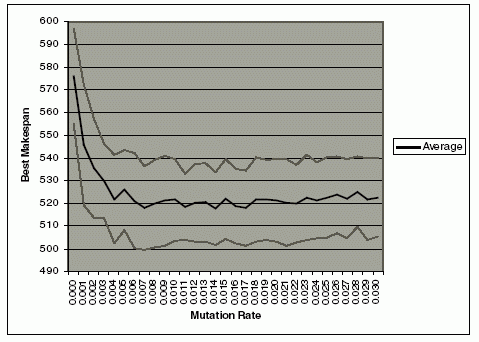
Рис. 6. Влияние мутаци на велечину времени решения

Оператор кроссинговера и оператор мутации для нового представления хромосомы и их подходящих норм были также представлены. От проводимых экспериментов, опытным путем показано, что новое представление хромосомы производит список с более коротким временем решения. При использовании Хромосомы D, с высоким переходом (> 0.85) и нулевой мутацией, пока равновесие не достигнуто, затем сопровождается регенерацией, и заявлением мутации (приблизительно 0.006 к 0.017) в предыдущем пункте перехода равновесия (или больше) произвело бы более низкое среднее число времени рещшения.

Ссылки

1.Jain A.S. and Meeran S., “Deterministic Job-Shop Scheduling: Past, Present and Future”, In European Journal of Operation Research, 113 (2), 390-434, 1998.
2.Pinedo, M., Chao, X., Operations scheduling with applications in manufacturing and services, McGraw-Hill, Chapter 1, 2 – 11, 1999.
3.Gambardella, L. M., Mastrolilli, M., Rizzoli, A. E., Zaffalon, M., “An optimization methodology for intermodal terminal management”, In Journal of Intelligent Manufacturing, 12, 521-534, 2001.
4.Jansen K., Mastrolilli M., Solis-Oba R., "Approximation Algorithms for Flexible Job Shop Problems", In Proceedings of Latin American Theoretical Informatics (LATIN'2000), LNCS 1776, 68-77, 1999.
5.Chen, H., Ihlow, J., and Lehmann, C., “A genetic algorithm for flexible job-shop scheduling”, In Proceedings of IEEE International Conference on Robotics and Automation, 2, 1120 – 1125, 1999.
6.Mesghouni K., Hammadi S., Borne P., “Evolution programs for job-shop scheduling”, In Proc. IEEE International Conference on Computational Cybernetics and Simulation, 1, 720 -725., 1997.
7.Kacem I., Hammadi S. and Borne P., “Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems”, In IEEE Transactions on Systems, Man and Cybernetics, 32(1), 1-13, 2002.
8.Paredis, J., Exploiting constraints as background knowledge for genetic algorithms: A case-study for scheduling, Ever Science Publishers, The Netherlands, 1992.
9.Ho N. B. and Tay J. C., “GENACE: An Efficient Cultural Algorithm for Solving the Flexible Job-Shop Problem”, accepted for publication in IEEE Congress of Evolutionar Computation 2004.
10.Fisher, H., Thompson, G.L., “Probabilistic learning combinations of local job-shop scheduling rules”, Industrial Scheduling, Prentice Hall, Englewood Cliffs, New Jersey, 225-251,1963.
11.Lin, S., and Kernighan, B. W., “An effective heuristic for traveling salesman problem”, In Operations Research, 21, 498-516, 1973.
12.Syswerda, G., Schedule optimization using genetic algorithms, Ed. L Davis (New York: Van Nostrand Reinhold) 332-349, 1991.