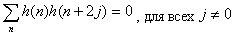
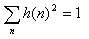
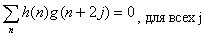
Источник: IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 25, NO. 5, MAY 2003
Аннотация
Классификация текстур на изображении, особенно тех, которые расположены под различными углами и в разном масштабе, является важной проблемой в анализе и классификации изображения. Эта статья предлагает эффективную схему классификации текстур, инвариантных к вращению и масштабированию, используя лог-полярные вейвлет-сигнатуры. Выделение признаков, инвариантных масштабированию и вращению, для данного изображения включает применение лог-полярного преобразования для устранения влияния вращения и масштабирования, но в то же самое время производит сдвинутое по рядам лог-полярное изображение, которое затем передается к адаптивному вейвлет-преобразователю, инвариантному сдвигу рядов, чтобы устранить эффекты сдвига рядов.
Таким образом, выходные коэффициенты вейвлета инвариантны к вращению и масштабированию. Адаптивное вейвлет-преобразование, инвариантное сдвигу рядов, весьма эффективно только с O(n*log(n)) сложностью. Вектор признаков доминирующих лог-полярных энергетических вейвлет-сигнатур, извлеченных из каждой подполосы коэффициентов вейвлета, создан классификации текстур, инвариантных к вращению и масштабированию. В экспериментах был использован классификатор Махаланобиса для классификации набора из 25 отличных природных текстур, выбранных из альбома Бродаца. Экспериментальные результаты, основанные на различных тестовых наборах данных для изображений с различными углами поворота и масштабами, показывают, что предложенная схема классификации, использующая лог-полярные вейвлет-сигнатуры, превосходит по быстродействию два других метода классификации текстуры. Точность метода для изображений, находящихся под различными углами поворота и в различном масштабе, составляет 90.8%, демонстрируя, что извлеченные энергетические сигнатуры являются эффективным для признаков, инвариантных к вращению и масштабированию. Относительно устойчивости к шуму схема классификации также превосходит другие методы.
1. Введение
Анализ текстуры играет очень важную роль в компьютерном представлении и распознавании изображений, так как большинство реальных объектов состоит из различных видов поверхностей текстуры. Текстура является признаком нижнего уровня изображения, и существует вокруг всех нас. Существует много различных приложений, основанных на анализе текстуры, включая медицинское отображение, дистанционное реагирование, индустриальный контроль, сегментацию документа, восстановление изображения и т.д. [1]. Анализ текстуры был изучен широко в течение более чем трех десятилетий. Первые подходы для классификации текстуры основывались на статистическом анализе текстур первого и второго порядка и на стохастических моделях, таких как модели случайных полей Гаусса и Маркова и авторегрессии [2]. Недавнее развитие пространственного частотного анализа на основе фильтров Габора [3], [4], вейвлет-преобразования [5], [6] и вейвлет-контуров [7] предоставляет хорошие аналитические инструментальные средства для анализа и классификации текстуры. Результаты экспериментов показывают, что эти методы могут достигнуть высокой степени точности.
Несмотря на такое разнообразие разработанных методов, большинство из них предполагает, что изображение не подвержено повороту или масштабированию. Однако это утверждение в основном не верно по отношению к практическим примерам, поэтому нельзя говорить об объективности таких методов.
Р.Кашьяп и А.Хотанзад [8] были одними из первых, кто осознал важность классификации текстур, инвариантных к вращению и масштабированию, и кто разработал круговую авторегрессионную (АР) модель. В их экспериментах были достигнуты хорошие результаты с маленькой базой данных из 12 текстур Бродаца.
М.Леун и А.Петерсон [9] предложили умственный подход преобразования, который оценивал масштаб и вращение текстуры первым прохождением спектра текстуры через лог-полярные фильтры Габора. Однако, это включает высокую вычислительную сложность, если количество классов текстуры или размер текстуры является большим.
Ф.Кохен и М.Пател [10] расширили двумерную модель случайного поля Гаусса и Маркова функцией вероятности, чтобы включить и оценивать параметры масштаба и вращения. Они утверждали, что достигли хороших результатов при использовании текстур девяти классов, взятых из базы данных Бродаца.
Дж.Йоу и Кохен [11] использовали алгоритм настройки с попыткой применить единственную маску свертки для сегментации и классификации текстур, подверженных повороту и масштабированию. Не так давно стали использовать многоканальные фильтры Габора для извлечения признаков текстур изображения, инвариантных к изменению угла поворота и масштаба [12], [13], [14], [15].
Р.Портер и Н.Канаджара [15] также использовали стандартное дискретное вейвлет-разложение с объединенными противоположными сигнатурами энергии в качестве признаков для классификации текстур, инвариантных к вращению и масштабированию.
Дж.-Л.Чен и А.Кунду [16], В.Ву и С.Вей [17] используют разложение подполосы и метод скрытой модели Маркова (СММ) для достижения инвариантности к повороту и масштабированию с помощью контролируемого изучения. Хотя они сообщили о достижении высоких результатов классификации, в их работах существуют некоторые недостатки. Так как стандартная подполоса и вейвлет-разложение чувствительны к вращению и масштабированию, то с увеличением количества классов не может сохраняться высокая степень точности.
Дж.Хайлей и Б.Манжунат [18] используют модель Габора полного пространственно-частотного вейвлета для классификации текстур, инвариантных к вращению и масштабированию, с очень перспективными результатами. Однако, здесь требуется высокая вычислительная сложность для выделения признаков.
С.-Д.Ким и С.Удпа [19] предложили для классификации текстур вращаемые вейвлет-фильтры, полученные вращением на 45o стандартного двумерного дискретного вейвлет-фильтра. Но, эти вращаемые фильтры являются инвариантными не ко всем углам вращения.
В общем, для многих разработанных методов классификации текстур, инвариантных к вращению и масштабированию существуют ограничения, включающие извлечение большого количества признаков текстуры и/или требуют высокой вычислительной сложности. Кроме того, многие из этих схем классификации, которые по утверждению их создателей были способными достигнуть высокой степени точности, основаны на экспериментах на маленьком наборе выбранных классов изображения.
Была неизвестна точность при увеличении количества классов или при использовании различных классов текстур. В этой статье предлагается эффективная схему классификации текстур, инвариантных к вращению и масштабированию, использующую лог-полярные вейвлет сигнатуры. Выделение признаков, инвариантных вращению и масштабированию, для данного изображения включает применение лог-полярного преобразования для того, чтобы устранить эффекты вращения и масштабирования, но в то же время производит лог-полярное изображение со сдвигом рядов, которое затем передается к адаптивному вейвлет-преобразователю, инвариантному сдвигу рядов, для устранения эффекта сдвига рядов.
Таким образом, выходные коэффициенты вейвлета инвариантны к вращению и масштабированию. Тогда для каждой подполосы этих коэффициентов вейвлета вычислена сигнатура энергии. Наконец, для уменьшения размерности признака, только самые доминирующие лог-полярные энергетические вейвлет-сигнатуры выбраны в качестве характеристического вектора для классификации текстур, инвариантных к вращению и масштабированию. Предложенный лог-полярный признак вейвлета был хорошо проверен с использованием классификатора Махаланобиса для того, чтобы классифицировать набор из 25 отличающихся между собой природных текстур, выбранных от альбома Бродаца.
План данной статьи организован в следующем порядке: В следующем разделе мы кратко вводим и рассматриваем стандартные методы 2-мерной вейвлет-пакетной декомпозиции. В разделе 3 мы представляем предложенную нами схему для извлечения инвариантных к вращению и масштабу логарифмически-полярных вейвлет сигнатур из любых изображений. Результаты классификации для разных энергетических шкал и разного количества преобладающих энергетических сигнатур по пяти наборам данных представлены в разделе 4. Сравнение качества классификации и помехоустойчивости нашего метода и другими существующими также рассматриваются в разделе 4.
2. Стандартное двумерное вейвлет-пакетное преобразование
Стандартное двумерное вейвлет-пакетное преобразование является обобщением двумерного дискретного вейвлет-преобразования (ДВП), которое предлагает более богатый диапазон возможностей для анализа изображения. В анализе ДВП изображение разложено на приблизительное и три детальных изображения. Приблизительное изображение в свою очередь само разбивается на приблизительное и детальное изображения второго уровня. Процесс рекурсивно повторяется. Таким образом, существует (n+1) возможных способов разбиения или кодирования изображения для n-уровневой декомпозиции. В двумерном вейвлет-пакетное преобразовании эти три детальные изображения так же, как и приблизительное изображение, могут быть раздроблены. То есть, существует 4n различных путей кодирования изображения, что обеспечивает лучший результат анализа изображения. Стандартое двумерное вейвлет-пакетное преобразование может быть описано парой квадратурных зеркальных фильтров (КЗФ) H и G [20]. Фильтр H – это низкоуровневый фильтр с конечным импульсом отклика, обозначенный h(n). Высокоуровневый фильтр G с конечным импульсом отклика определен:
| g(n)=(-1)nh(1-n), для всех n. | (1) |
Низкоуровневый фильтр выбран для того, чтобы удовлетворить следующим условиям ортонормального представления:
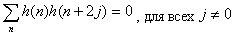 |
(2) |
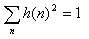 |
(3) |
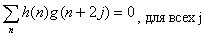 |
(4) |
Двумерная вейвлет-пакетная декомпозиция дискретного изображения X размером NxM до уровня p+1 рекурсивно определена через коэффициенты уровня p следующим образом:
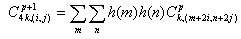 |
(5) |
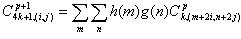 |
(6) |
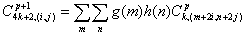 |
(7) |
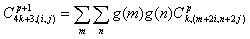 |
(8) |
где 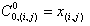 определяется уровнями интенсивности изображения X. На каждом шаге производится декомпозиция изображения
определяется уровнями интенсивности изображения X. На каждом шаге производится декомпозиция изображения 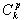 на 4 четырехмерных изображения
на 4 четырехмерных изображения  . Этот алгоритм декомпозиции представлен на рис.1.
. Этот алгоритм декомпозиции представлен на рис.1.
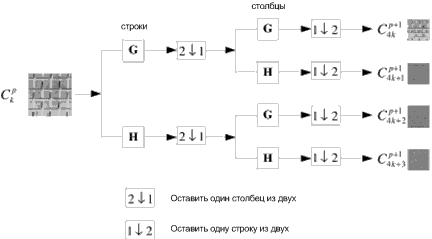
Рисунок 1. Декомпозиция изображения с совместным использованием фильтров H и G
Ряды изображения 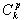 образуют свертку с одномерным фильтром, остальные ряды сохраняются. Затем столбцы результирующих изображений образуют свертку с другим одномерным фильтром, остальные ряды сохраняются.
образуют свертку с одномерным фильтром, остальные ряды сохраняются. Затем столбцы результирующих изображений образуют свертку с другим одномерным фильтром, остальные ряды сохраняются.
3. Лог-полярные энергетические вейвлет-сигнатуры, обеспечивающие инвариантность к вращению и масштабированию
ДВП, как показано в литературе [5], [6], [20], является полезным для анализа изображения благодаря вейвлетам, имеющим конечную продолжительность, которые обеспечивают и частоту и пространственное местоположение и эффективное выполнение. Иерархическое одномерное дискретное вейвлет-преобразование использует пару высокоуровневого и низкоуровневого фильтров, полученных из функций вейвлет для декомпозиции первоначального сигнала в две подполосы: детальную и приблизительную, соответственно. Процесс декомпозиции рекурсивно применяется к иерархии. Если был выбран ортонормальный базис вейвлета, то вычисленные коэффициенты независимы и обладают отличительным признаком первоначального сигнала. Однако известно, что один из главных недостатков ДВП – это недостаток инвариантности к смещению входного сигнала из-за двумерной структуры разложения вейвлета [29]. И для двух входных сигналов/изображений, двумерное ДВП также чувствительно к изменениям положения; то есть те же самые изображения с различными углами поворота могут иметь различные коэффициенты вейвлета. Основная причина состоит в том, что эффективное выполнение двумерного ДВП требует применения группы фильтров вдоль строк и столбцов изображения [20]. Из-за разделенности фильтров, разделенное двумерное ДВП строго ориентировано в горизонтальном и вертикальном направлениях. Это делает едва возможным извлечение признаков, инвариантных вращению, из коэффициентов вейвлета.
По алгоритму данного метода происходит извлечение лог-полярных энергетических вейвлет-сигнатур, инвариантных к вращению и масштабированию, для данного изображения, которые могут быть получены с помощью лог-полярного преобразования на изображении, а затем с помощью адаптивного вейвлет-преобразования, инвариантного сдвигу рядов (как показано в рис. 2).
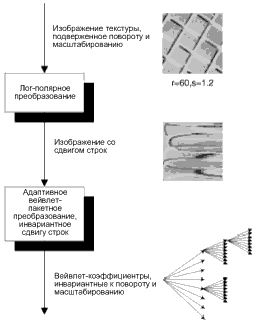
Рисунок 2. Выделение вейвлет-коэффициентов, инвариантных к повороту и масштабированию, из изображения текстуры, подверженной повороту и масштабированию
Затем, для каждого поддиапазона выходных коэффициентов вейвлет, инвариантных к вращению и масштабированию вычисляют энергетические сигнатуры, согласно определённой шкале энергии. Для уменьшения размерности признака, только самые существенные лог-полярные энергетические вейвлет-сигнатуры отбираются в качестве вектора признаков для классификации текстур, инвариантных к повороту и масштабированию. Ниже приведены детали.
3.1. Лог-полярное преобразование
На первом шаге предложенного метода вейвлет-сигнатур, инвариантных к повороту и масштабированию, используется лог-полярное преобразование для устранения эффектов поворота и масштаба во входном изображении, конвертируя его в соответствующее лог-полярное изображение. Такое лог-полярное изображение не зависит от изменения поворота и почти не зависит от изменения масштаба, так как изображения одного размера в разных масштабах имеют разный уровень видимой насыщенности (рис. 3).

Рисунок 3. Пример текстуры (D1) из альбома Бродаца с разными углами поворота (r в градусах) и в разном масштабе (s) и их лог-полярные изображения
Однако результирующее лог-полярное изображение сдвинуто по рядам. Алгоритм лог-полярного преобразования разделён на 2 основных этапа. На первом этапе радиус наибольшего круга внутри данного изображения используется как сканирующая линия выборки (сэмплирования) S раз от 0o до 360o для получения эквивалентной Sx[N/2] полярной формы (см. рис. 4a). Так, формально, полярная форма p(a,r) данного NxN изображения f(x,y) может быть вычислена как:
 |
(9) |
для а=0,…,S-1, и r=0,…,[N/2]-1.
На втором этапе логарифмическая функция применяется ко всем значениям радиуса в полярной форме, и их выходные величины квантуются на R состояний. Получаем SxR лог-полярное изображение для заданного NxN изображения, как показано на Рис. 4b.
 |
(10) |
для i=0,…,S-1, и j=0,…,R-1.
Рисунок 4. Лог-полярное преобразование NxN изображения (f(x,y)) в SxR лог-полярное изображение (lp(i,j)) посредством сначала (а) использования радиуса в качестве разделяющей линии для разбивки окружности на N частей для получения полярной формы p(a,r), а затем с помощью квантования логарифмических значений для получения лог-полярного изображения
Как показано на рис.3, лог-полярные изображения текстуры с разными углами поворота и масштабами кажутся имеющими только сдвиг по рядам, когда сравниваются с лог-полярным изображением (исходной) неповёрнутой текстуры. Лог-полярное преобразование достаточно эффективно со сложностью вычислений O(n), (где n – количество пикселей в исходном изображении).
3.2. Адаптивное вейвлет-пакетное преобразование, инвариантное к сдвигу по рядам
После применения операции лог-полярного преобразования, изображение с измененным углом поворота и масштабом должно быть превращено в соответствующее лог-полярное изображение, инвариантное к вращению и почти инвариантное к масштабу. Однако любые изменения положения приведут к сдвигу ряда в лог-полярном изображении. Общий подход вейвлет-пакетного преобразования или декомпозиции, как показано в разделе 2, эффективно рассчитывает вейвлет-пакетные коэффициенты со сложностью О(n) (где n – число пикселей в данном изображении)[29]. Однако полученные таким образом вейвлет-пакетные коэффициенты не инвариантны к сдвигу. Предложенные многочисленные алгоритмы инвариантной к сдвигу декомпозиции [21,22,23,24,25] являются инвариантными к сдвигу и по рядам, и по столбцам. Тем не менее, эти алгоритмы, генерирующие больше избыточных вейвлет коэффициентов, не подходят для выходного изображения со сдвигом по ряду, создаваемого нашим лог-полярным преобразованием. Нам нужна вейвлет-пакетная декомпозиция, которая должна быть инвариантной только к сдвигу по рядам, для более эффективного создания менее избыточных вейвлет-коэффициентов. Следовательно, мы предлагаем адаптивное вейвлет-преобразование, инвариантное к сдвигу рядов, для решения проблемы, создаваемой лог-полярным преобразованием изображения, и в результате мы можем получить инвариантность к вращению и масштабу.
В нашем адаптивном вейвлет-пакетном преобразовании, инвариантном к сдвигу рядов, мы используем пару квадратурных зеркальных фильтров (КЗФ) (как описывалось в разделе 2), для получения ортонормального представления. Для того, чтобы получить инвариантность к сдвигу рядов, мы используем метод периодической краевой обработки и создаем избыточный набор вейвлет-пакетных коэффициентов для одного дополнительного дугового сдвига ряда. То есть, на каждом уровне р+1, мы рассчитываем четыре периодических изображения без сдвига:
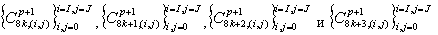
следующим образом:
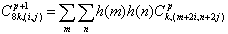 |
(11) |
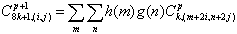 |
(12) |
 |
(13) |
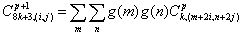 |
(14) |
где  задается уровнями серого цвета изображения х.
задается уровнями серого цвета изображения х.
Поскольку мы просто держим один из двух рядов, эти коэффициенты кажутся такими же, если  сдвинуто по дуге на 0,2,4…..2n рядов.
сдвинуто по дуге на 0,2,4…..2n рядов.
Для того, чтобы получить инвариантность ряда к сдвигу, нам нужно рассчитать другие четыре периодических изображения, каждое со сдвигом на один ряд:

следующим образом:
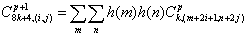 |
(15) |
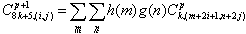 |
(16) |
 |
(17) |
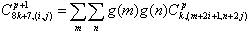 |
(18) |
Подобным образом эти коэффициенты окажутся теми самыми, если  сдвинется по дуге на 1, 3, 5, 2n+1 рядов, соответственно.
сдвинется по дуге на 1, 3, 5, 2n+1 рядов, соответственно.
На каждом шагу мы разбиваем изображение на 8 четверть-размерных изображения 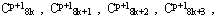
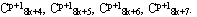 Этот алгоритм аналогичен стандартному ВПП и может быть проиллюстрирован блочной диаграммой на рис.5. Ряды изображения
Этот алгоритм аналогичен стандартному ВПП и может быть проиллюстрирован блочной диаграммой на рис.5. Ряды изображения 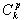 сначала свёртываются одномерным фильтром и остальные ряды запоминаются. Затем колонки полученного изображения свёртываются другим одномерным фильтром и также исходные запоминаются. Итак, 4 четверть-размерных изображения
сначала свёртываются одномерным фильтром и остальные ряды запоминаются. Затем колонки полученного изображения свёртываются другим одномерным фильтром и также исходные запоминаются. Итак, 4 четверть-размерных изображения 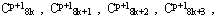 сгенерированы. Тот же процесс повторяется ещё для одного изображения
сгенерированы. Тот же процесс повторяется ещё для одного изображения 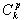 , только со сдвинутым вниз одним рядом, для получения других изображений
, только со сдвинутым вниз одним рядом, для получения других изображений 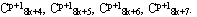
Набор из всех сгенерированных периодических изображений может быть организован в форме окта-дерева с полной рекурсивной декомпозицией (как показано на рис.5).
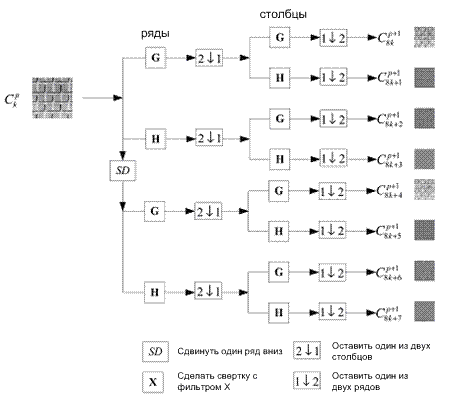
Рисунок 5. Декомпозиция дискретного изображения 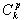 на 8 четверть-размерных сдвинутых по рядам инвариантных изображений
на 8 четверть-размерных сдвинутых по рядам инвариантных изображений 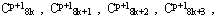
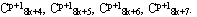 с помощью использования фильтров H и G.
с помощью использования фильтров H и G.
Очевидно, что это окта-дерево даёт более полное описание изображения по сравнению с представлением стандартного ВПП в виде квадро-дерева (Раздел 2). В целях повышения эффективности и локаничности представления и, в то же время, получения инвариантности к сдвигу по ряду, мы построили лучший базис представления изображения, инвариантного к сдвигу по ряду, чем ВПП. Согласно с предложением Кофмана и Виккерхозера мы адаптивно выбираем некоторые поддиапазоны для дальнейшей декомпозиции, вместо декомпозиции каждого поддиапазона. Основная идея – вычислить цену информации для каждого поддиапазона и сравнить ее с аналогичной полусуммой всех поддиапазона следующего уровня декомпозиции. Если цена информации текущего поддиапазона меньше полусуммы информации всех поддиапазонов следующего уровня, то текущий поддиапазон далее не декомпозируется; иначе мы декомпозируем текущий поддиапазон далее и делаем аналогичные сравнения до тех пор, пока не достигнут максимальный уровень декомпозиции. Следовательно, самый лучший базис представления может быть получен эффективным рекурсивным процессом отбора, который определяет лучшую декомпозицию изображения, базируясь только на локальной минимизации функции цены информации. Пусть лучший базис представления уровня j будет 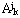 , тогда лучший базис
, тогда лучший базис 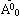 для изображения x может рекурсивно быть вычислен как:
для изображения x может рекурсивно быть вычислен как:
 |
(19) |
Рекурсивное вычисление продолжается до максимального или указанного уровня J, где
 |
(20) |
Функция цены информации должна быть аддитивной, где М(0)=0 и 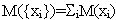 . Несколько полезных примеров включают:
. Несколько полезных примеров включают:
 |
(21) |
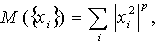 |
(22) |
 |
(23) |
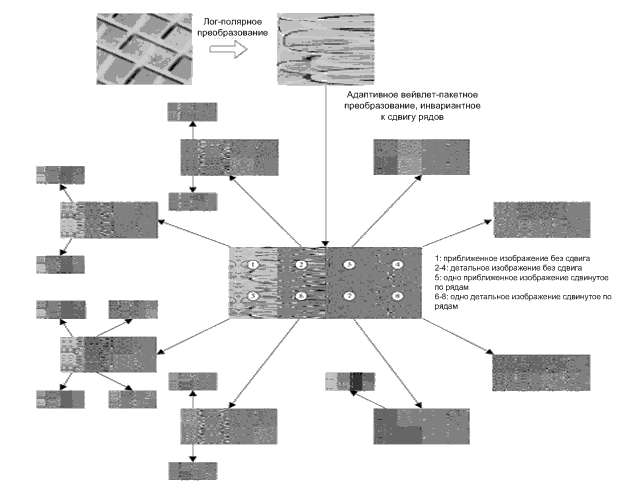
Рисунок 6. Лучшее представление базиса полярного изображения заданного изображения (D1 с углом поворота 120o и масштабом 1.2)
Схемы на рис. 6 и 7 показывают 2 примера представления лучшего базиса для лог-полярных изображений текстуры Бродаца D1 с разным углом поворота и масштабом. Их лучший базис представления оптимален согласно данной функции стоимости информации. Хотя исходное изображение на рис. 6 очевидно повёрнуто и отличается масштабом от такого же на рис. 7, их соответствующие лог-полярные изображения идентичны за исключением сдвига по ряду, и их структура адаптивного ВПП инвариантного к сдвигу по рядам одинакова, не считая взаимного расположения некоторых ветвей и подветвей.
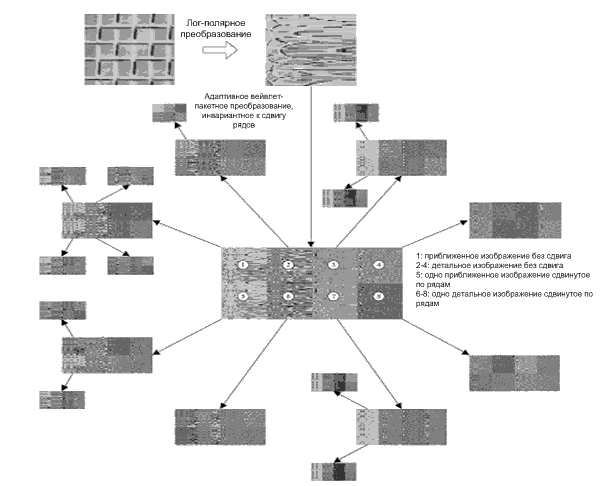
Рисунок 7. Лучшее представление базиса полярного изображения заданного изображения (D1 без поворота и изменения масштаба)
Для подсчёта сложности вычислений создаем восемь двумерных периодических изображений от одного уровня до более высокого. Таким образом, для достижения инвариантности к сдвигу по рядам, мы имеем 8l=2l*4l двумерных периодических изображений для декомпозиции до уровня l, что в 2l раз превышает сложность стандартного ВПП. Однако эта декомпозиция работает эффективно. Переходя от уровня к уровню, мы удваиваем количество двумерных периодических изображений и уменьшаем в 4 раза размер каждой из них. Применяя эту процедуру рекурсивно ко всем уровням, мы получаем вейвлет-пакетные коэффициенты для всех циклических сдвигов по ряду в log(N) шагах с общей сложностью O(n*log(n)), (где n – количество пикселей исходного изображения).
3.3. Выделение сигнатур, инвариантных к вращению и масштабу
Имея ряды сдвинутого лог-полярного изображения, полученного из лог-полярного преобразования в качестве входной информации для адаптивного вейвлет-пакетного преобразования, инвариантного к сдвигу рядов, можно решить проблему сдвига рядов лог-полярного изображения. Итак, генерируемые коэффициенты являются инвариантными к вращению и почти инваринантными к масштабу. Однако большое количество вейвлет-коэффициентов не пригодно для устойчивой текстурной классификации. Итак, мы уменьшаем характеристику размерности вейвлет коэффициентов, рассчитывая энергетические сигнатуры для каждой подполосы. Таким образом, число энергетических сигнатур равно числу подполос, генерируемых адаптивным вейвлет-пакетным преобразованием сдвига ряда. Однако, число энергетических сигнатур для текстурной классификации непостоянное, и может быть очень большим. Как предложили Чанг и Кои [5], большинство каналов с доминантной частотой предоставляют очень полезную информацию для дискриминационных текстур. Следовательно, мы классифицируем все энергетические сигнатуры и выбираем лишь М сигнатур с наиболее доминантной энергией (с самой высокой величиной энергии) в качестве вектора признаков. Детали этого алгоритма представлены ниже.
3.3.1. Алгоритм выделения лог-полярных энергетических вейвлет-сигнатур, инвариантных к вращению и масштабу
Шаг 1. Для данного изображения N x N, выполняем лог-полярное преобразование (как описано в разделе 1), для получения лог-полярного изображения S x R, где мы допускаем, что S = R = N.
Шаг 2. Применяем адаптивное вейвлет-пакетное преобразование, инвариантное к сдвигу ряда (как описано в разделе 2) к лог-полярному изображению, создавая m подполос вейвлет-коэффициентов 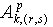 , где p*log2(N),
, где p*log2(N),  и r, s=0,1,…,2logN-p-1.
и r, s=0,1,…,2logN-p-1.
Шаг 3. Рассчитываем энергетические сигнатуры:

с несколькими измерениями энергии для каждой подполосы вейвлет-коэффициентов 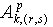 , где n=1,…,m.
, где n=1,…,m.
Шаг 4. Располагаем все энергии сигнатур в нисходящем порядке, согласно их значениям 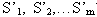 и выбираем первые М сигнатур с наиболее доминантной энергией (с самыми высокими значениями энергии) как вектор признаков,
и выбираем первые М сигнатур с наиболее доминантной энергией (с самыми высокими значениями энергии) как вектор признаков, 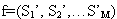 , где
, где  .
.
Шаг 5. Получаем характерный вектор f в качестве энергетических сигнатур, инвариантных к вращению и масштабу, для данного изображения.
4. Результаты сравнения эффективности методов
Для сравнения эффективности рассматриваемого метода был были проведены эксперименты по распознаванию текстур изображений с помощью следующих методов: методу, использующему лог-полярные энергетические вейвлет-сигнатуры, методу многоканальной фильтрации Габора и методу стандартных энергетических вейвлет-сигнатур. Результаты классификации были взяты из экспериментов этими тремя методами с одинаковыми входными данными и с использованием одного и того же классификатора Махаланобиса.
4.1. Результаты cравнения методов
В таблице 1 приведены сравнительные результаты классификации предложенным методом и другими двумя методами, инвариантными к вращению: методом многоканальной фильтрации Габора [12], [13] и стандартным методом сигнатур энергии вейвлет-пакета [6]. Экспериментальные результаты показывают, что предложенный метод классификации текстуры, использующий сигнатуры энергии полярного вейвлета превосходит по быстродействию другие два метода на всех наборах данных. В большинстве случаев усовершенствование весьма существенно. Предложенный метод очень эффективен. Он имеет вычислительную сложность O (n*log (n)) (где n - количество пикселей в изображении), а также высокую точность на трех различных наборах данных, хотя в некоторых случаях потребовалось больше признаков.
Таблица 1. Сравнительные результаты работы по трем методам: методу, использующему лог-полярные энергетические вейвлет-сигнатуры, методу многоканальной фильтрации Габора и методу стандартных энергетических вейвлет-сигнатур.
| Метод лог-полярных энергетических вейвлет-сигнатур | Метод многоканальной фильтрации Габора | Метод стандартных энергетических вейвлет-сигнатур | |
| Набор данных №1 (поворот и масштабирование) | 90.8% | 82.5% | 64.6% |
| Количество признаков | 96 | 48 | 64 |
| Набор данных №2 (только поворот) | 93.8% | 88.2% | 68.5% |
| Количество признаков | 64 | 48 | 64 |
| Набор данных №3 (только масштабирование) | 88.6% | 72.4% | 75.8% |
| Количество признаков | 96 | 48 | 64 | Набор данных №4 (только поворот) | 100% | 87.5% | 66.5% |
| Количество признаков | 64 | 48 | 64 | Набор данных №5 (только масштабирование) | 82.5% | 70.5% | 73.0% |
| Количество признаков | 96 | 48 | 64 |
| Приблизительная сложность | О(n*log(n)) | O(n2) | О(n*log(n)) |
4.2. Устойчивость к шуму
Были проведены эксперименты для исследования устойчивости вышеупомянутых трех различных методов классификации к шуму. Данные были введены с добавлением белого Гауссовского шума с нулевым средним значением и дисперсией, в зависимости от требуемого отношения сигнал-шум, равного n, к типовым изображениям текстуры от набора данных 1. Результаты, полученные вследствие эксперимента, представлены на графике на рис. 8, который демонстрирует, что предложенный метод, использующий энергетические сигнатуры лог-полярного вейвлет-пакетного преобразования, всегда превосходит по быстродействию другие два метода при различном уровне шума. Другое наблюдение состоит в том, что предложенный метод допускает шум в большей степени, чем другие два метода.
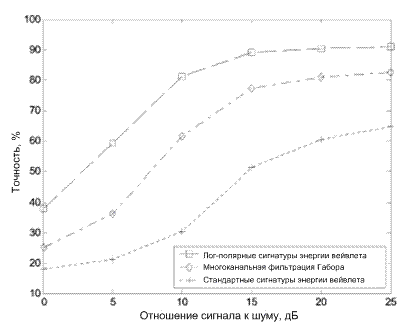
Рисунок 8. Сравнительные результаты работы по трем методам: методу, использующему энергетические сигнатуры лог-полярного вейвлет-пакетного преобразования, методу многоканальной фильтрации Габора и методу стандартных сигнатур энергии вейвлета; при условии, что входное изображение подвержено различным уровням шума
Список источников
[1] M. Tuceryan and A.K. Jain, “Texture Analysis,” Handbook of Pattern Recognition and Computer Vision, pp. 235-276, World Scientific, 1993.
[2] R.W. Conners and C.A. Harlow, “A Theoretical Comparison of Texture Algorithms,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 2, pp. 204-222, May 1980.
[3] A.C. Bovik, M. Clark, and W.S. Geisler, “Multichannel Texture Analysis Using Localized Spatial Filters,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 12, Jan. 1990.
[4] A. Teuner, O. Pichler, and B.J. Hosticka, “Unsupervised Texture Segmentation of Images Using Tuned Matched Gabor Filters,” IEEE Trans. Image Processing, vol. 6, no. 4, pp. 863-870, 1995.
[5] T. Chang and C.C.J. Kuo, “Texture Analysis and Classification with Tree-Structured Wavelet Transform,” IEEE Trans. Image Processing, vol. 2, pp. 429-441, Apr. 1993.
[6] A. Laine and J. Fan, “Texture Classification by Wavelet Packet Signatures,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 15, no. 11, pp. 1186-1191, Nov. 1993.
[7] M. Unser, “Texture Classification and Segmentation Using Wavelet Frames,” IEEE Trans. Image Processing, vol. 4, pp. 1549- 1560, Nov. 1995.
[8] R.L. Kashyap and A. Khotanzed, “A Model-Based Method for Rotation Invariant Texture Classification,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 8, pp. 472-481, July 1986.
[9] M. Leung and A.M. Peterson, “Scale and Rotation Invariant Texture Classification,” Proc. Int’l Conf. Acoustics, Speech, and Signal Processing, pp. 461-165, 1991.
[10] F.S. Cohen, Z. Fan, and M.A. Patel, “Classification of Rotated and Scaled Textured Images Using Gaussian Markov Random Field Models,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 13, no. 2, pp. 192-202, Feb. 1991.
[11] J. You and H.A. Cohen, “Classification and Segmentation of Rotated and Scaled Textured Images Using Texture ‘Tuned’ Masks,” Pattern Recognition, vol. 26, pp. 245-258, 1993.
[12] G.M. Hayley and B.M. Manjunath, “Rotation Invariant Texture Classification using Modified Gabor Filters,” Proc. Int’l Conf. Image Processing ’95, pp. 262-265, 1994.
[13] S.R. Fountain and T.N. Tan, “Extraction of Noise Robust Invariant Texture Features via Multichannel Filtering,” Proc. Int’l Conf. Image Processing ‘97, vol. 3, pp. 197-200, 1997.
[14] S.R. Fountain, T.N. Tan, and K.D. Baker, “A Comparative Study of Rotation Invariant Classification and Retrieval of Texture Images,” Proc. Ninth British Machine Vision Conf., pp. 266-275, Sept. 1998.
[15] R. Porter and N. Canagarajah, “Robust Rotation-Invariant Texture Classification: Wavelet, Gabor Filter and GMRF Based Schemes,” IEE Proc.—Vision Image Signal Processing, vol. 144, no. 3, June 1997.
[16] J.-L. Chen and A. Kundu, “Rotation and Greyscale Transform Invariant Texture Identification using Wavelet Decomposition and HMM,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 16, no. 2, 1994.
[17] W.R. Wu and S.C. Wei, “Rotation and Gray-Scale Transform- Invariant Texture Classification Using Sprial Resampling, Subband Decomposition, and,” IEEE Trans. Image Processing, vol. 5, Oct. 1996.
[18] G.M. Hayley and B.M. Manjunath, “Rotation Invariant Texture Classification Using a Complete Space-Frequency Model,” IEEE Trans. Image Processing, vol. 8, Feb. 1999.
[19] S.-D. Kim and S. Udpa, “Texture Classification Using Rotated Wavelet Filter,” IEEE Trans. Systems, Man, and Cybernetics, Part A, vol. 30, no. 6, pp. 847-852, Nov. 2000.
[20] S. Mallat, “A Theory for Multiresolution Signal Decomposition: The Wavelet Decomposition,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 11, no. 7, pp. 674-693, July 1989.
[21] G. Beylkin, “On the Representation of Operators in Bases of Compactly Supported Wavelets,” SIAM J. Numerical Analysis, vol. 6, no. 6, pp. 1716-1740, Dec. 1992.
[22] R.R. Coifman and D.L. Donoho, “Translation-Invariant De- Noising,” Wavelet and Statistics, Lecture Notes in Statistics, A. Antoniadis and G. Oppenheim, ed., Springer-Verlag, pp. 125-150, 1995.
[23] J. Liang and T.W. Parks, “A Translation-Invariant Wavelet Representation Algorithm with Applications,” IEEE Trans. Signal Processing, vol. 44, Feb. 1996.
[24] J.C. Pesquet, H. Hrim, and H. Carfantan, “Time-Invariant Orthonormal Wavelet Representations,” IEEE Trans. Signal Processing, vol. 44, Aug. 1996.
[25] I. Cohen, S. Raz, and D. Malah, “Orthonormal Shift-Invariant Wavelet Packet Decomposition and Representation,” Signal Processing, vol. 57, no. 3, pp. 251-270, Mar. 1997.
[26] R.R. Coifman and M.V. Wickerhauser, “Entropy-Based Algorithms for Best Basis Selection,” IEEE Trans. Information Theory, vol. 38, no. 2, pp. 713-718, Mar. 1992.
[27] I. Daubechies, “Orthonormal Bases of Compactly Supported Wavelets,” Comm. Pure and Applied Math., vol. 41, pp. 909-996, Nov. 1988.
[28] R.R. Coifman and D.L. Donoho, “Translation-Invariant De-Noising,” Wavelet and Statistics, Lecture Notes in Statistics, A. Antoniadis and G. Oppenheim, ed., Springer-Verlag, pp. 125-150, 1995.
[29] I. Daubechies, Ten Lectures on Wavelets, CBMS-NSF Regional Conf. Series in Applied Math., SIAM Press, 1992.
[30] G. Beylkin, “On the Representation of Operators in Bases of Compactly Supported Wavelets,” SIAM J. Numerical Analysis, vol. 6, no. 6, pp. 1716-1740, Dec. 1992.
[31] P. Brodatz, Texture: A Photographic Album for Artists and Designers. New York: Dover, 1966.
[32] R.J. Schalkoff, Pattern Recognition: Statistical, Structural, and Neural Approaches. New York: John Wiley and Sons, 1992.