к оси x:Источник: http://lear.inrialpes.fr/people/zhang/ECCV_paper.pdf [154 КБ]
Аннотация
В этой статье, мы представляем теоретически и в вычислительном отношении простой, но эффективный подход для классификации текстур, инвариантных к изменению угла поворота. Этот метод основан на новых текстурных признаках, извлеченных из спектра. Признаки текстуры, инвариантные к повороту, вычисляются на основании полученных сигнатур.
Признаки протестированы на 1000 примеров изображений с произвольными углами поворота из 20 классов текстур Бродаца. Результаты сравнения показывают, что данный метод очень эффективен в классификации текстур изображений, инвариантных к изменению угла поворота.
I. Введение
Анализ текстуры – фундаментальная проблема в обработке изображения, машинном зрении и его использовании в объектном распознавании, дистанционном воздействии, восстановлении изображения на основе его содержания и так далее. Это исследовательская тема активно развивается уже более трех десятилетий. Многочисленные методы были предложены в открытой литературе [1] [2] [3]. Большинство существующих методов делает явное или неявное предположение, что производится распознавание текстур на изображениях расположенных всегда одинаково (например, неизменный масштаб и отсутствие угла поворота). Однако во многих практических исследованиях, таких как восстановление изображения на основе его содержания, полученные изображения часто подвержены геометрическим искажениям, включая сдвиг, вращение, масштабирование и наклон. Кроме того, учитывая изображение текстуры, согласно опыту или познавательной теории, геометрически искаженные текстуры всегда выглядят именно так, как их наблюдает человек. В связи с этим признаки текстуры должны обязательно быть инвариантными к изменению угла поворота. Недавние обзоры проводимых исследований по этой важной теме могут быть найдены в [7] [8].
Анализ Фурье рассматривается как мощный инструмент в инвариантном анализе текстуры. Недавние исследования по этой теме могут быть найдены в [13] [14] [15]. В данной статье предлагается новый метод для простого в вычислительном отношении, но эффективного распознавания текстуры, инвариантной к вращению. Производиться расчет функции распределения сигнатуры, базируемой на представлении спектра повернутого изображения текстуры. Применяя преобразование Фурье на этой функции, была достигнута инвариантность к повороту. Мы исследуем полноценность этих предложенных признаков на базе данных изображений 1000 текстур с произвольными углами поворота. Обширное сравнительное исследование признаков Габора показывает, что предложенный алгоритм очень эффективен в инвариантной классификации текстуры.
II. Текстурные сигнатуры, инвариантные к вращению
В этом разделе предлагается алгоритм вычисления новых сигнатур текстуры, оценивается ее работа в фиксировании свойств текстуры и далее это разрабатывается, для достижения инвариантности к вращению.
1. Проекция
Пусть f(x,y) – первоначальное изображение текстуры. Определим проекцию f(x,y) на линию l под углом к оси x:
| где |  |
(1) |
Если =0, то получаем вертикальную проекцию на ось x:
 |
(2) |
Функция проекции может получить периодическую функцию текстур в разных направлениях. Это проиллюстрировано на рис.1 (здесь =0).
Проекция функции f(x,y) на линию, расположенную под углом, может быть оценена с помощью ее Фурье-версии на линию под углом .
Пусть функция fr(xr,yr) является повернутой версией функции f(x,y). Тогда взаимосвязь этих двух изображений формулируется следующим образом:
| fr(xr,yr)=f(x,y); |  |
(3) |
Известно, что при повороте первоначальной текстуры на какой-то угол спектр частотной области также сдвигается на этот угол. Это свойство поворота преобразования Фурье. Связь между спектром первоначального и повернутого изображения описывается следующим образом:
 |
(4) |
где 
- преобразование Фурье первоначальной текстуры f(x,y),
- преобразование Фурье текстуры fr(xr,yr),
- обратная транспонированная матрица матрицы R.
Одномерное преобразование Фурье для выражения (2):
 |
(5) |
Полученное выражение может быть записано в другой форме:
 |
(6) |
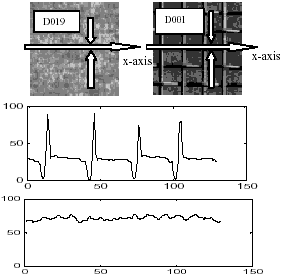
Рисунок 1. Иллюстрация свойств проекции в измерении параметров текстуры
2. Текстурные характеристики, инвариантные к повороту
Пусть 
, 
– преобразование Фурье проекции f(x,y) на линию под углом ; 
– преобразование Фурье проекции fr(xr,yr) на линию под углом 
. Их связь представляет собой:
| = |
(7) |
Центральный момент выражения (7):
 |
(8) |
где 
- средние значения 
.
Вычислим спектр сигнатур с углом и (=+
):
 |
(9) |
Таким образом получили спектральные сигнатуры направления T(). Очевидно, что текстурная сигнатура зависит от поворота и является функцией от с периодом 2
.
T()=T(), если -=. Это подразумевает, что поворот входного изображения f(x,y) на угол эквивалентен сдвигу его спектральных сигнатур на такое же число вдоль оси направления. Связь между T() и T() показана на рис.2.
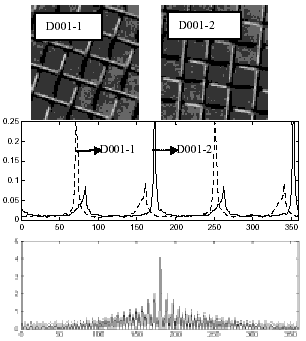
Рисунок 2. Иллюстрация влияния поворота на сигнатуры
Схематическая диаграмма получения признаков текстуры, инвариантных к вращению представлена на рис.3.
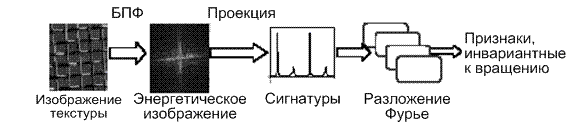
Рисунок 3. Схематическая диаграмма получения признаков текстуры, инвариантных к вращению
III. Экспериментальные результаты
Чтобы проверить эффективность предложенных признаков для анализа текстур, инвариантных вращению, был выполнен эксперимент на 20 изображениях текстур, выбранных из альбома Бродаца (рис. 4).
Рисунок 4. 20 образцов текстур Бродаца, использованных для классификации текстур, инвариантных к вращению
Необходимо отметить, что, если текстуры изотропны или случайны, любые описатели текстуры будут инвариантны к вращению [9]. Каждое изображение текстуры размера 512x512 произвольно повернуто на любой из 15 вариантов углов, из которых извлечены подизображения размера 128x128. Таким образом, для этого эксперимента создана база данных из 1000 изображений. База данных из 140 экземпляров (по 7 на каждый класс текстуры) используется для обучения и сохранения (860 изображений, 43 для каждой текстуры), для тестирования. Из каждого изображения извлечено распределение сигнатуры текстуры T (), и его амплитуда Фурье используются как признаки текстуры, инвариантной к вращения. Первые 7 величин выбраны для создания 7-мерных векторов признаков для использования в классификации текстуры, инвариантной к вращению. Для измерения подобия между текстурами рассчитано Эвклидово расстояние.
Используется классификатор К-ближайших соседей. Здесь оптимальное значение K выбрано равное 10, согласно точности. Получена средняя правильная норма распознавания 98.95%. Результаты классификации каждого класса текстуры показаны на рис. 5. Это явно показывает перспективную эффективность предложенных признаков для классификации текстур, инвариантных вращению.
Рисунок 5. Результаты классификации с помощью фильтров Габора и сигнатур
В нашей предыдущей работе, мы предложили описатели текстуры инварианта вращения [4] [5] [9] и провели сравнительное изучение четырех методов инвариантной классификации текстуры (метод Габора, скрытая модель Маркова, обрабатывающий модель контурного атрибута, и круговую одновременную авторегрессионную модель) [5]. Подробности могут быть найдены в этих статьях. В этой статье мы не должны повторить эти сравнения. Мы только сравниваем наш метод с признаками Габора, инвариантными повороту, который был указан самым эффективным в [5] [6]. Мы делаем это, чтобы далее прояснить работу нового предложенного признака в классификации текстур, инвариантных вращению. Мы выполняем это сравнительное изучение при том же самом условии, упомянутом выше. Средняя точность классификации 98.90% получена при использовании признаков Габора. Наше изучение указывает, что метод достигает почти тех же самых результатов классификации, что и метод Габора и Хьюмана (рис. 6).
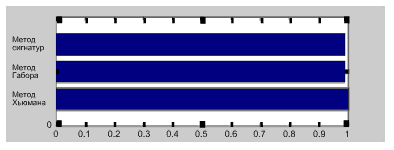
Рисунок 6. Сравнение точностей представления по методам сигнатур, Габора и Хьюмана
Однако вычислительная сложность метода Габора намного выше, чем предложенного алгоритма. Кроме того, недостатком метода Габора, инвариантного к вращению, является проблема осуществления выборки канала Габора. Результаты, приведенные на рис. 7, показывают, что работа метода Габора ухудшается, поскольку интервал осуществления выборки между каналами Габора увеличивается (или количество каналов Габора уменьшается).
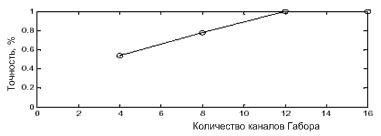
Рисунок 7. График зависимости точности метода Габора от количества каналов Габора
Для достижения более высокой точности интервал канала Габора должен быть меньшим. Это увеличит сложность вычислений. Необходимо отметить, что количество наложений между каналами Габора также увеличится в пространственной и частотной области [11]. С этой точки зрения предложенный новый алгоритм имеет меньшую вычислительную сложность.
IV. Заключения и будущая работа
Мы предложили теоретически и в вычислительном отношении простой алгоритм извлечения характеристик текстуры, которые могут фиксировать свойства текстуры. Новая характеристика вычислена в спектральной области. Это было разработано, чтобы получить характеристики текстуры, инвариантной к вращению. Инвариантные характеристики получены на основании расширения характеристик Фурье. Наше сравнительное изучение показывает его высокую эффективность в классификации текстур, инвариантных к вращению. Следует отметить, что при наличии теней, образованных вследствие неровности поверхности, вращение может пагубно изменить изображение, и работа этого метода может быть ухудшена. Дальнейшее исследование должно включить устойчивость метода к шуму изображения, его использование в восстановлении изображений с различными углами поворота и классификации текстуры, инвариантной к аффинным преобразованиям.
Список источников
[1] M. Tuceryan and A.K. Jain, Texture Analysis, in Handbook of Pattern Recognition and Computer Vision (C. H. Chen, et. al., Eds.), 1993, pp.235-276.
[2] A.R. Rao, Taxonomy for Texture Description and Identification. Springer Verlag: Berlin, 1990.
[3] F. Tomita, and S. Tsuji, Computer Analysis of Visual Textures, Hingham, MA: Kluwer Academic, 1990
[4] S.R. Fountain, T.N. Tan, “Efficient Rotation Invariant Texture Features for Content-based Image Retrieval”. Pattern recognition, Vol. 31,No. 11 1998, pp1725-1732.
[5] S.R Fountain, T.N. Tan, “A Comparative Study of Rotation Invariant Classification and Retrieval of Texture images. Proc. of BMVC, Vol. 1, pp. 266-275. 1998
[6] R. Porter, N. Canagarajah, "Robust rotation invariant texture classification: wavelet, Gabor filter, and GMRF based schemes," IEE Proc. –Vision Image Signal Processing, Vol. 144, No. 3, pp. 180-188, June, 1997.
[7] T.N. Tan, "Geometric transform invariant texture analysis," SPIE. Vol. 2488, pp475-485, 1995.
[8] J.G. Zhang and T.N. Tan, "Brief review of invariant texture analysis methods," Pattern Recognition, Vol. 35/3, pp.735-747, 2002.
[9] T.N.Tan, "Rotation invariant texture features and their use in automatic script identification," IEEE Trans. Pattern Analysis and Machine Intelligence Vol.20, No.7, pp. 751-756, July 1998.
[10] P. Brodatz, Textures: A Photographic Album for Artist and Designer. Dover, New York (1966).
[11] A.K. Jain, F. Farrokhnia "Unsupervised texture segmentation using Gabor filters", Pattern Recognition, Vol. 24, No. 12, pp.1167-1186, 1991.
[12] M. Pietikainen, T. Ojala, Z. Xu, Rotation-Invariant texture classification using feature distributions, Pattern Recognition 33 (2000) pp. 975-985
[13] H. Aof, F.Deravi, "Circular neighborhood and 1-D DFT feature for texture classification and segmentation", IEE Proc. Vision Image Signal Processing 145(3) pp. 167-172,1998
[14] "One dimensional Fourier transform coefficient for rotation invariant texture classification," Proc. SPIE 2908, pp.152-159, 1996.
[15] O. Alata, C. Cariou, C. Ramananjarasoa, M. Najim, "Classification of rotated and scaled textures using HMHV spectrum estimation and the fourier mellin transform", IEEE Proc. ICIP, pp.53-56, 1998
[16] A. Kadyrov and M.Petrou, "The Trace Transform and its applications", IEEE Pattern Analysis and Machine Intelligence, Vol. 23 No. 8, pp.811-828, 2001.