Источник: Обработка изображений, ICIP '04, Международная Конференция, Выпуск 1, 24-27 октября 2004, стр.:227 - 230
Аннотация
Сегментация изображения может рассматриваться как процесс классификации областей изображения в группы с общими свойствами (то есть текстуры). Возникновение трудностей состоит в том, что общая текстура может классифицироваться по-разному при рассмотрении ее в различных масштабах и с разными углами поворота. Эта статья представляет вектор признаков, основанный на методе КВП-ДД (комплексное вейвлет-преобразование «двойного дерева»), который является инвариантным к изменению угла поворота и масштаба. Многообещающие результаты сегментации изображения (без корректировки неклассифицированных областей) демонстрируют пригодность этого вектора признаков в представлении текстуры.
1. Введение
Текстурный анализ включает представление характеристик областей изображения в форме, которая может с готовностью определить их соответствующие классы. Это развилось за эти годы от статического критерия областей изображения (то есть разницы) к более поздним методам, где критерий структуры может базироваться на коэффициентах фильтрации с помощью вейвлет-преобразования Габора или дискретного вейвлет-преобразования (ДВП). Более недавние методы включают методы, инвариантные к изменению угла поворота и масштаба. Значение лучшего представления заключается в том, что сегментация достигнута точно за один шаг классификации признаков.
Вследствие исследований человеческой зрительной системы предполагается, что зрение базируется на реакции клеток с характеристикой, подобной двумерным вейвлетам Габора. Впоследствии, наблюдалось развитие методов представления текстуры, основанных на вейвлетах Габора. Ученый Р.Манталкар и другие описали способ определения признаков на основе преобразования Габора, инвариантного к изменению угла поворота и масштаба, путем объединения быстрого преобразования Фурье (БПФ) с вейвлетами Габора. Они используют этот вектор признаков при восстановлении изображений, в библиотеке изображений текстур, представленных в различных масштабах и с различными углами поворота.
Реально оцененные вейвлет-преобразования испытывают недостаток инвариантности и поэтому они предоставляют недостаточный выбор для представленной текстуры. Чтобы преодолеть эту проблему, Н.Кингсбери разработал комплексное вейвлет-преобразование «двойного дерева», чтобы показать приблизительную инвариантность к сдвигам изображения. П.Хилл объединил быстрое преобразование Фурье с двумерным комплексным вейвлет-преобразованием «двойного дерева», чтобы получить признаки, инвариантные к вращению, для представления текстуры.
Эта статья расширяет понятия, описанные П. Хиллом, о создании вектора признаков для текстуры, инвариантного к изменению угла поворота и масштаба. Она начинается с описания некоторых свойств КВП-ДД. Затем следует обсуждение процессов, необходимых для модификации этого преобразования для его использования в фильтрах, пригодных для анализа изображений в разных масштабах. Далее показано, как инвариантность к изменению масштаба достигается с помощью вектора признаков, и затем представлены результаты сегментации изображения. В конце обсуждается значение особенностей инвариантности к изменению масштаба для представления текстуры, и рассматриваются положительные результаты от получения их с помощью КВП-ДД.
2. Свойства комплексного вейвлет-преобразования «двойного дерева»
Комплексное вейвлет-преобразование «двойного дерева» является формой дискретного вейвлет-преобразования, которое производит комплексные оценочные коэффициенты. Это осуществляется с помощью двойных деревьев фильтров, которые независимо производят реальные и мнимые ответы. Свойства КВП-ДД включают:
Для двумерной функции фильтры подобны фильтрам Габора, поэтому КВП-ДД может быть эффективным способом произвести коэффициенты отклика подобные коэффициентам Габора. На каждом уровне производится 6 подполос, которые обнаруживают признаки, различающиеся на 30o.
3. ДВП# в анализе изображений с изменяющимся масштабом
ДВП обеспечивает инструмент многомасштабного анализа для рассмотрения сигналов. Это преобразование может быть представлено как полосно-пропускающий фильтр, фильтры которого чувствительны к частотам по двухэлементным шкалам. На каждом уровне анализа, входной сигнал разложен на функции по базису вейвлет:
где Ф – материнская вейвлет-функция, S – целое число для обозначения масштаба, К – число, определяющее сдвиг. Функции базиса вейвлета для КВП-ДД определяются таким же образом, как и для ДВП.
Для анализа признаков, инвариантного к изменению масштаба, используются фильтры, равные по амплитуде на каждом уровне анализа, поэтому можно убрать множитель 
. Получается новое семейство функций базиса вейвлета:
Ф#s,k(x)=Ф(2-sx-k).
Нет необходимости изменять фильтры для КВП-ДД. Нужно только умножить выходные коэффициенты на . Обозначим КВП-ДД# и ДВП# как преобразования, использующие Ф#s,k(x) для своих базисных функций вейвлета.
4. Инвариантность к масштабированию
Если проанализировать две синусоидальные волны (частота одной в два раза больше частоты другой), то получим, что значения откликов одинаковы в обоих случаях (рис.1(a) и (b)). Это иллюстрирует независимость величины отклика от масштаба.
Если изменения происходят не по двумерной шкале, то это изменение не отражается (рис.1(с)). Величина отклика при быстром преобразовании Фурье, примененная к коэффициентам на рис.1(a) будет эквивалентна на рис.(b) и отлична на рис.1(с). Это то, что мешает достигнуть инвариантности к изменению масштаба при любых факторах изменения масштаба.
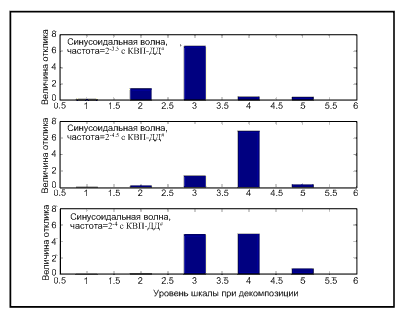
Рисунок 1. Изображение отклика |КВП-ДД#| на синусоидальные сигналы, где a) частота=2-3.5, b) частота=2-4.5, c) частота=2-4.
Достоинство использования вейвлет Габора вместе с методом ДВП# состоит в том, что анализируемый сигнал на должен быть представлен на двумерной шкале. Пользователь имеет возможность разделения частоты и определения степени наложения полос. Например, в научных работах Н.Жанга и В.Леова ими были подобраны такие значения: коэффициент наложения полос равен 0.75, а разделение частот равно 0.75 октав.
Во всех формах ДВП имеются фильтры, расположенные в двумерной шкале, с целью минимизировать избыточность и увеличить эффективность. Предлагается добавить фильтры в двумерные шкалы в КВП-ДД# для того, чтобы достигнуть необходимого уровня анализа, предоставленного вейвлетами Габора.
Необходимый фильтр должен быть размещен посередине между двумерными шкалами в КВП-ДД# (эта середина находится в логарифмическом представлении по двумерным шкалам). Фильтрация в этих серединных частотах эквивалентна применению КВП-ДД# к сигналу, масштабируемому с коэффициентом 2-1/2.
Если теперь в этих условиях повторить эксперимент с синусоидальными волнами разной частоты, то можно убедиться в эквивалентности величин отклика на всех трех рисунках (рис.2(a),(b),(c)).
Рисунок 2. Изображение отклика |КВП-ДД#| на синусоидальные сигналы, где a) частота=2-3.5, b) частота=2-4.5, c) частота=2-4.
Коэффициенты при инвариантности к изменению масштаба создаются из амплитуд отклика БПФ. Они равняются u=(…u-2, u-1, u0, u1, u2…) и имеют свойство: u-i= u*i. Если |u-n|=|un|, то коэффициенты избыточности |u1|, |u2|,… могут быть отброшены.
5. Инвариантность к повороту и изменению масштаба двумерных изображений
Пусть RI – rotation invariant (инвариантные к повороту) и SI – scale invariant (инвариантные к масштабированию) признаки были получены из КВП-ДД#2 (двумерное КВП-ДД#) и использованы для представления изображения. Шаги получения этих признаков из изображения I0(x,y) следующие:
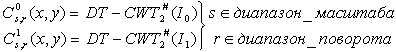
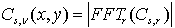для измерения поворота.
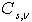и сохраняем в 
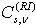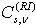. до количества рядов и столбцов изображения I0. 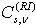производим преобразование 
для измерения масштаба.
и сохраняем в 
.Результат: Получили двумерный вектор признаков, построенный на u и 
, инвариантный к изменению масштаба и угла поворота для каждых x и y в . С помощью кластеризации этих двумерных векторов признаков мы можем сегментировать изображение I0 на области.
Кроме этого можно получить признаки, инвариантные к изменению амплитуды.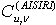 
можно вычислить путем деления на элемент CD в . Этот признак обеспечивает инвариантность к изменению яркости, поворота и масштаба при классификации текстур [13, 14].
6. Результаты сегментации изображения
Результат сегментации зависит от количества уровней декомпозиции и количества классов. На рис. 3 показан результат сегментации изображения, используя рассмотренный метод, инвариантный изменению угла поворота и масштаба. Здесь изображена группа зебр на фоне растительности.
Рисунок 3. Сегментация изображения зебр (3 уровня декомпозиции, 2 класса)
Рисунок 4. Сегментация изображения леопарда (3 уровня декомпозиции, 3 класса)
На рис. 4 показан результат сегментации изображения леопарда, наполовину спрятанного в траве.
7. Обсуждение
Текстурный анализ, инвариантный к изменению масштаба, требует новых методов представления текстуры, так как многие традиционно используемые методы для этого не совсем подходят. Например, мера грубости текстуры может использоваться как мера различия между областями изображения. Так как грубость – функция масштаба, то она не является подходящей для использования в качестве признака текстуры, инвариантного к изменению масштаба.
Использование КВП-ДД имеет преимущество вычислительной эффективности перед традиционными методами, основанным на вейвлетах Габора. Признаки текстуры, инвариантные к изменению угла поворота и масштаба, показывают хорошую пригодность для представления текстур и общее наблюдение заключается в том, что области сгруппированы в классы пятнистых, полосатых, плоских или перекрещивающихся текстур. Это может говорить о том, что рассмотренный метод несколько связан с познанием более высокого уровня.
8. Заключение
В модели машинного зрения сегментация текстуры является одним из возможных способов получения значения из изображения. Эта статья представляет методику, основанную на КВП-ДД, для генерирования описания текстуры неопределенного угла поворота и масштаба. Как следствие, это дает способность идентифицировать текстуру независимо от ее рассматриваемого угла поворота или масштаба. Для проверки этих свойств инвариантности к углу поворота и масштабу производится сегментация изображения с помощью классификации области по признакам. Экспериментальные результаты доказывают пригодность этого метода для лучшего представления текстур.
Использованные источники:
[1] N. Kingsbury, "Complex Wavelets for Shift Invariant Analysis and Filtering of Signals," Applied and Computational Harmonic Analysis, vol. 10, pp. 234-253, May, 2001.
[2] M. M. Leung and A. M. Peterson, "Scale and Rotation Invariant Texture Classification," in Proc. Asilomar Conf. Signals, Syst & Computers, Pacific Grove, CA, USA, Oct, 1992.
[3] Y. Wu and Y. Yoshida, "An Efficient Method for Rotation and Scaling Invariant Texture Classification," in Proc. ICASSP, Detroit, MI, USA, May, 1995.
[4] O. Alata, et al., "Classification of Rotated and Scaled Textures using HMHV Spectrum Estimation and the Fourier-Mellin Transform," in Proc. ICIP, Talence, France, Oct, 1998.
[5] D. G. Sim, et al., "Translation, Scale, and Rotation Invariant Texture Descriptor for Texture-Based Image Retrieval," in Proc. ICIP, Vancouver, BC, Canada, Sept, 2000.Ы
[6] T. S. Lee, "Image Representation using 2D Gabor Wavelets," IEEE Trans. PAMI, vol. 18, pp. 959-971, Oct, 1996.
[7] B. S. Manjunath and W. Y. Ma, "Texture Features for Browsing and Retrieval of Image Data," IEEE Trans. PAMI, vol.18, pp. 837-842, Aug, 1996.
[8] B. S. Manjunath, et al., "Color and Texture Descriptors," IEEE Trans. CSVT, vol. 11, pp. 703-715, June, 2001.
[9] R. Manthalkar, et al., "Rotation and Scale Invariant Texture Classification using Gabor Wavelets," in Proc. Int. Workshop Texture Analysis and Synthesis. Copenhagen, Denmark: HWU, June, 2002, pp. 87-90.
[10] P. R. Hill, et al., "Rotationally Invariant Texture Features using Dual-Tree Complex Wavelet Transform," in Proc. ICIP, vol. 3. Vancouver, BC, Canada: IEEE, Sept, 2000, pp. 901-904.
[11] A. Graps, "An Introduction to Wavelets," IEEE Computational Science & Engineering, vol. 2, pp. 50-61, 1995.
[12] N. Zhang and W. K. Leow, "Perceptually Consistent Segmentation of Texture using Multiple Channel Filter," in Proc. Asian Conf on Computer Vision. Hong Kong, China: HKUST, Jan, 1998, pp. 17-24.
[13] T. Ojala, et al., "Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns," IEEE Trans. PAMI, vol. 24, pp. 971-987, July, 2002.
[14] L. Wang and G. Healey, "Using Zernike Moments for the Illumination and Geometry Invariant Classification of Multispectral Texture," IEEE Trans. IP, vol. 7, pp. 196-203, Feb, 1998.