Source: Image Processing, 2004. ICIP '04. 2004 International Conference on Volume 1, 24-27 Oct. 2004 Page(s):227 - 230 Vol. 1
ABSTRACT
Image segmentation can be viewed as the process of classifying regions in a picture into groups with common properties (i.e. texture). A difficulty arising is that common texture can be classified differently when viewed at different scales and rotated viewpoints. This paper presents a feature vector based on the DT-CWT (dual-tree complex wavelet transform [1]) that is invariant to scale and rotation. The promising image segmentation results (without cleaning misclassified regions) demonstrate the suitability of this feature vector in representing texture.
1. INTRODUCTION
Texture analysis involves representing the characteristics of image regions in a form that can readily determine their respective classes. It has evolved over the years from a statistical measure of image regions (i.e. variance) to more recent times where the measure of texture may be based on the coefficients of filtering with DWTs or 2D Gabor wavelets. More recent techniques include those methods that are scale and rotation invariant [2-5]. The implication of better representation is that segmentation is achieved accurately in a single step of feature classification.
Research into the human visual system suggests that vision is based on responses of cells with a characteristic similar to 2D Gabor wavelets [6]. Subsequently, we have seen the evolution of texture representation techniques based on Gabor wavelets [7] with one considered as a texture descriptor for MPEG-7 [8]. Manthalkar, et al. describe a way of generating Gabor based features invariant to scale and rotation by combining the FFT with Gabor wavelets [9]. They use this feature vector in the application of content based image retrieval to a library of texture images presented at different scales and rotations.
Real valued DWTs lack shift invariance and therefore make a poor choice for representing texture. To overcome this problem, Kingsbury designed the DT-CWT [1] to exhibit approximate shift invariance. Hill, et al. combined the FFT with the 2D DT-CWT to derive features invariant to rotation for texture representation [10].
This paper extends the concepts described by Hill et al. to generate a feature vector for texture, invariant to both scale and rotation. It starts by describing some of the properties of the DT-CWT and follows by discussing the processes needed to modify this transform into filters suitable for multi-scale analysis. The subsequent section exposes how scale invariance is achieved by our feature vector and we then look at the results of image segmentation. A final section discusses the significance of scale invariant features for texture representation and looks at the benefits of deriving them from the DT-CWT.
2. PROPERTIES OF THE DT-CWT
The DT-CWT is a form of DWT that generates complex valued coefficients. It is implemented with dual-trees of filters that independently generate the real and imaginary responses. Properties of the DT-CWT include:
In 2D, the filters are similar to Gabor filters, so the DT-CWT can be an efficient way of generating Gabor-like response coefficients. At each level, it generates 6 subbands that detect features spaced 30o apart [1].
3. THE DWT#: FOR ANALYSIS ACROSS SCALES
The DWT provides a multi-scale analysis tool for looking at signals. It can be viewed as a band-pass filter whose filters are sensitive to frequencies over dyadic scales. At each level of analysis, the input signal is decomposed into functions of wavelet basis functions
such that Ô defines the mother wavelet, the integer s describes the scale of analysis while k defines the shift [11]. The wavelet basis functions for the DT-CWT are scaled in the same way as the DWT.
For scale invariant feature analysis, we desire filters that are equal in amplitude at each level of analysis and so we remove the scaling factor of 2-s/2. The new family of wavelet basis functions is generated by
Ô#s,k(x)=Ô(2-sx-k).
Fortunately, we do not have to modify the filters in the DT-CWT but instead, we only need to multiply the DT-CWT output coefficients by 2-s/2. For ease of reference, we denote DT-CWT# and DWT# as the transforms that use Ô#s,k(x) for their wavelet basis functions.
4. SCALE INVARIANCE
By default, a dyadic scale change in the input signal into the DT-CWT# and DWT# will result in a coefficient shift in the scale dimension. Let us analyse two sine waves, one twice the frequency of another. The profile across scale dimension of DT-CWT# magnitude response on each are shown in Figures 1(a) and (b). It illustrates dyadic scaling being equivalent to shifting in scale dimension.
Over non-dyadic scale changes, that shift does not occur and is illustrated in Figure 1(c). The magnitude response of the FFT applied to coefficients in Figure 1(a) will be equal over Figure 1(b) but different over Figure 1(c). This is precisely what prevents us from achieving scale invariance over arbitrary zoom factors.
The advantage with using Gabor wavelets over DWT# techniques is that signal analysis need not be performed on dyadic scales. The user has the option of specifying the frequency separation and the degree of overlap between the filter’s half-peak supports. The design of the filter used by Manthalkar, et al. had minimal overlap between bands and had a frequency separation of 0.7 octaves [9].
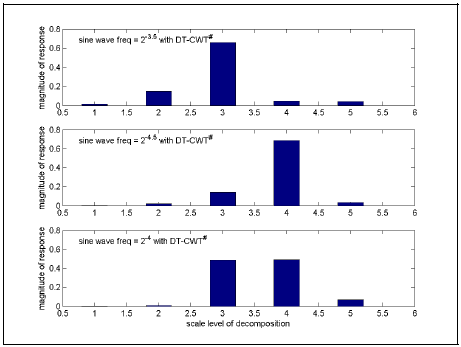
Figure 1: Profile of |DT-CWT#| response to sine waves of (a) freq = 2-3.5, (b) freq= 2-4.5 and (c) freq = 2-4.
In an application for image segmentation, Zhang and Leow generated feature vectors derived from a Gabor wavelet design with overlapping half-peak supports [12]. Following their notation, an overlap factor of ? = 0.75 and frequency separation of 0.75 octaves were used. In both these instances (Manthalkar, et al. and Zhang and Leow), scale invariance was attributed to their filter design.
All forms of the DWT have filters spaced at dyadic scales to minimise redundancy and maximise efficiency. While redundancy is important for image compression, it bears less importance for the purposes of signal analysis. We propose filters be added in between those at dyadic scales in the DT-CWT# to achieve the level of scale-space analysis afforded by the Gabor wavelets. Fortunately, we need not modify the DT-CWT# to achieve that outcome.
The filter design we seek is one that places filters halfway between dyadic scales in the DT-CWT# (this midpoint is in logarithmic view over dyadic scales). Filtering at these midpoint frequencies is equivalent to applying the DT-CWT# over the signal scaled by a factor of 2-1/2. A single pyramid of results is formed by interleaving the two results of filtering by scale level of the coefficients.
The experiment with sine waves of different frequencies is repeated to illustrate scale invariance. Figures 2(a) and (b) confirm that dyadic scaling still results in shifting over scale dimension. The major improvement is in Figure 2(c) where the waveform being tracked is almost preserved and provides the basis for scale invariance.
FFT has a property that converts the effect of shifting in the time domain into a change of phase in the frequency domain. Scale invariant coefficients are generated from the amplitude of the FFT response. The output of the FFT generates coefficients u=(…u-2, u-1, u0, u1, u2…) and has the property, u-i= u*i. Since |u-n|=|un|, the redundant coefficients |u1|, |u2|, … can be safely discarded.
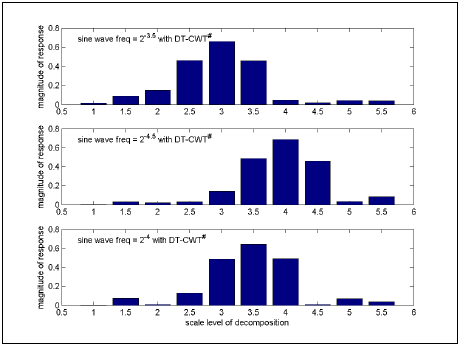
Figure 2: Profile of |DT-CWT#| response to sine waves of (a) freq = 2-3.5, (b) freq= 2-4.5 and (c) freq = 2-4.
5. SCALE & ROTATION INVARIANCE IN 2D
It is proposed that RI (rotation invariant) and SI (scale invariant) features be generated from the DT-CWT#2 (2D DT-CWT#) and used to represent texture. The steps that generate these features from image I0(x,y), are as follows:
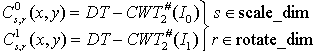
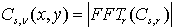over rotation dimension.
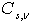relating to complex conjugates and store in 
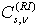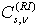. to number of rows and columns in image I0. 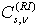pyramid, generate, 
over scale dimension.
relating to complex conjugates and store in 
.The result: there is a 2D feature vector spanning over u, 
that is invariant to scale and rotation for every x, y in . By clustering these 2D feature vectors, we can segment I0 into regions of similarity.
Through our design, each SIRI feature vector is invariant to scale and rotation. Furthermore, (outside this paper’s scope) the amplitude invariant feature,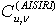 
may be derived by dividing all coefficients in by the DC component in . This feature provides illumination, rotation and scale invariant texture classification [13, 14].
6. RESULTS OF IMAGE SEGMENTATION
The results of segmentation depend primarily on how many levels of DT-CWT#2 decompositions L are used. The texture to be considered must be characterised within 2Lx2L pixels at most. High L results in better matching of textures over a greater number of scales while finer accuracy of segmentation is achieved when L is set low.
Two pictures will be used to illustrate the results of image segmentation using the SIRI feature vectors. The first one, in Figure 3 shows a group of zebras against a backdrop of vegetation. Figure 4 shows the second image and contains a leopard semi-camouflaged within a patch of grass. The segmentation process will involve classifying the SIRI features using k-means (without a post-processing stage).
Figure 3: Segmentation of zebras (L = 3, classes = 2).
Figure 4: Segmentation of leopard (L = 3, classes = 3).
Using DT-CWT#2 via L=3 decompositions and clustering with k-means to 2 classes, the zebras image is segmented into the classes shown in Figure 3. The top-right diagram in Figure 3 illustrates the pixel classes whilst those in the lower section reflect the textures that belong to those classes. Having all the zebras stripes grouped into a single class provides a good indication of scale and rotation invariance since the stripes vary in size and orientation.
Using DT-CWT#2 with L=3 and classifying with k-means to 3 classes generates the segmented regions shown in Figure 4. Segmentation of the background is easy because there is almost a complete absence of high frequency components. The true test is its ability to distinguish between grassy texture and spotty texture. It is interesting to note that the results of segmentation are fairly accurate. On close inspection, the grass seemingly misclassified as of leopard-like texture does indeed exhibit spottiness.
7. DISCUSSION
Scale invariant texture analysis requires new ways of representing texture but some techniques traditionally used as texture features are not suitable for scale invariant analysis. For example, the measure of texture coarseness can be used as a way of discriminating between image regions. Since coarseness is a function of scale it is not suitable for use as a scale invariant texture feature.
Using the DT-CWT has the advantage of computational efficiency over traditional techniques based on the Gabor wavelets. The scale and rotation invariant features detailed exhibit good suitability for texture representation and the general observation is that regions are grouped into classes of spotty, stripy, flat or crisscross textures. This may indicate that our scale and rotation features are somewhat associated with higher level cognition.
Future work will compare results from other methods of classification with those from k-means. Other techniques include statistical region shape models and methods that automatically cluster, for unsupervised segmentation.
8. CONCLUSION
In the model of computer vision, texture segmentation is one of the possible ways to derive meaning from images. This paper presents a technique based on the DT-CWT to generate a description of texture that is non-specific to orientation and scale. As a consequence it gives the ability to identify texture irrespective of its viewed orientation or scale. To test these properties of invariance to rotation and scale, we attempt to segment images by classifying regions based on the feature. The experimental results of segmentation are pleasing and suggest of the suitability of this new feature for better representing texture.
9. REFERENCES
[1] N. Kingsbury, "Complex Wavelets for Shift Invariant Analysis and Filtering of Signals," Applied and Computational Harmonic Analysis, vol. 10, pp. 234-253, May, 2001.
[2] M. M. Leung and A. M. Peterson, "Scale and Rotation Invariant Texture Classification," in Proc. Asilomar Conf. Signals, Syst & Computers, Pacific Grove, CA, USA, Oct, 1992.
[3] Y. Wu and Y. Yoshida, "An Efficient Method for Rotation and Scaling Invariant Texture Classification," in Proc. ICASSP, Detroit, MI, USA, May, 1995.
[4] O. Alata, et al., "Classification of Rotated and Scaled Textures using HMHV Spectrum Estimation and the Fourier-Mellin Transform," in Proc. ICIP, Talence, France, Oct, 1998.
[5] D. G. Sim, et al., "Translation, Scale, and Rotation Invariant Texture Descriptor for Texture-Based Image Retrieval," in Proc. ICIP, Vancouver, BC, Canada, Sept, 2000.Û
[6] T. S. Lee, "Image Representation using 2D Gabor Wavelets," IEEE Trans. PAMI, vol. 18, pp. 959-971, Oct, 1996.
[7] B. S. Manjunath and W. Y. Ma, "Texture Features for Browsing and Retrieval of Image Data," IEEE Trans. PAMI, vol.18, pp. 837-842, Aug, 1996.
[8] B. S. Manjunath, et al., "Color and Texture Descriptors," IEEE Trans. CSVT, vol. 11, pp. 703-715, June, 2001.
[9] R. Manthalkar, et al., "Rotation and Scale Invariant Texture Classification using Gabor Wavelets," in Proc. Int. Workshop Texture Analysis and Synthesis. Copenhagen, Denmark: HWU, June, 2002, pp. 87-90.
[10] P. R. Hill, et al., "Rotationally Invariant Texture Features using Dual-Tree Complex Wavelet Transform," in Proc. ICIP, vol. 3. Vancouver, BC, Canada: IEEE, Sept, 2000, pp. 901-904.
[11] A. Graps, "An Introduction to Wavelets," IEEE Computational Science & Engineering, vol. 2, pp. 50-61, 1995.
[12] N. Zhang and W. K. Leow, "Perceptually Consistent Segmentation of Texture using Multiple Channel Filter," in Proc. Asian Conf on Computer Vision. Hong Kong, China: HKUST, Jan, 1998, pp. 17-24.
[13] T. Ojala, et al., "Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns," IEEE Trans. PAMI, vol. 24, pp. 971-987, July, 2002.
[14] L. Wang and G. Healey, "Using Zernike Moments for the Illumination and Geometry Invariant Classification of Multispectral Texture," IEEE Trans. IP, vol. 7, pp. 196-203, Feb, 1998.