Преобразование Фурье
Анатолий КАРТАШКИН
Источник: http://www.n-t.ru/tp/iz/pf.htm
В основе преобразования Фурье (ПФ) лежит чрезвычайно простая, но исключительно плодотворная идея – почти любую периодическую функцию можно представить суммой отдельных гармонических составляющих (синусоид и косинусоид с различными амплитудами A, периодами Т и, следовательно, частотами ω). Пример одной из таких функций S(t), состоящей из гармоник Сi(t), приведен на рис. 1.
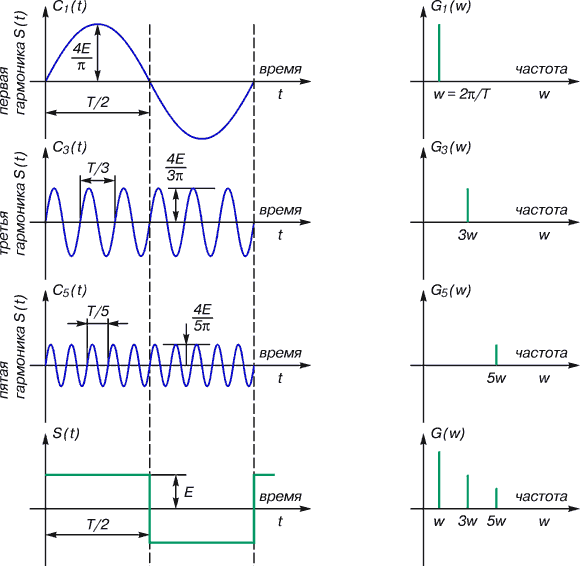
Рис. 1. Представление прямоугольного импульса суммой гармонических составляющих
Понятия «изобразить в частотной области некую функцию от времени» и «нарисовать спектр этой функции» – равнозначны. Если скользнуть по рис. 1 взглядом по горизонтали слева направо, то свершится переход от какой-либо функции времени к ее спектру – благодаря «магическому стеклу» ПФ. А нижняя часть рисунка есть иллюстрация одного из основных принципов ПФ – спектр суммарной функции времени равен сумме спектров ее гармонических составляющих.
Неоспоримым достоинством ПФ является его гибкость – преобразование может использоваться как для непрерывных функций времени, так и для дискретных. В последнем случае оно называется дискретным ПФ – ДПФ.
Для получения дискретной функции времени надо подвергнуть процессу дискретизации непрерывную функцию времени. Это изображено на рис. 2. Вырезаем отдельные значения из непрерывной функции, выстраивая дискретную функцию времени. Период одного цикла его работы Tд называется «периодом дискретизации», или «интервалом дискретности».
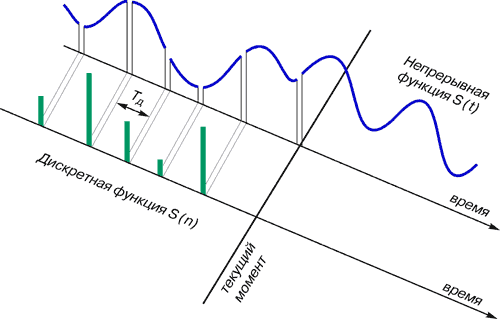
Рис. 2. Дискретное представление непрерывной функции
ПФ часто применяется при решении задач, возникающих в теории автоматического регулирования и управления, в теории фильтрации и т.д. Разберем один из примеров. Имеется некий линейный фильтр – изготовленный то ли в виде набора спаянных между собой резисторов, конденсаторов и катушек индуктивности, то ли в виде модульной конструкции интегральных микросхем. Известен также входной сигнал (на рис. 3 в качестве входного сигнала изображена дельта-функция, то есть импульс исчезающе короткой длительности и бесконечно большой амплитуды). Необходимо определить, какой сигнал появится на выходе нашего фильтра.
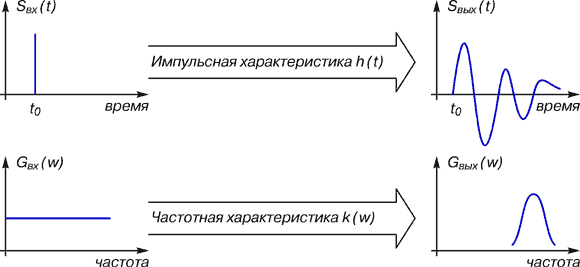
Рис. 3. Исследование линейного фильтра
Ход решения этой задачи зависит от того, какую позицию мы предпочтем. Выберем временной путь решения (верхняя половина рис. 4) – придется входной сигнал записать как функцию времени SBX(t) и использовать импульсную характеристику фильтра h(t), то есть математическую запись его работы во времени. Отправимся по частотному пути (нижняя половина рис. 4) – нужно будет оперировать уже не с самим входным сигналом, а с его спектром gbx(ω). Δа и алгоритм работы нашего фильтра потребуется представить в частотной области – в виде частотной характеристики K(ω). Δля этого воспользуемся помощью опять-таки «магического стекла» ПФ.
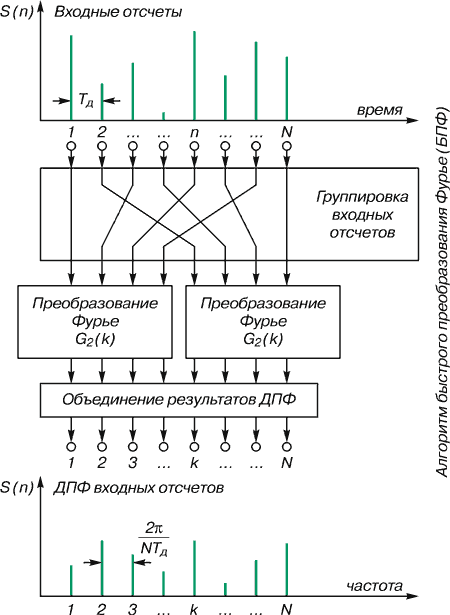
Рис. 4. Быстрое преобразование Фурье
Итак, два пути – какой из них избрать? По-видимому, тот, который проще. Во всяком случае, в большинстве практических задач предпочтение отдается частотному направлению.
Если выполнять ДПФ входной последовательности, так сказать, впрямую – строго по исходной формуле, то потребуется много времени (особенно если количество входных отсчетов велико). Конструктивнее использовать принцип «разделяй и властвуй», лежащий в основе алгоритма БПФ. Согласно ему входная последовательность делится на группы (например, четные и нечетные отсчеты), и для каждой из них выполняется ДПФ, а затем полученные результаты объединяются. В итоге получается ДПФ входной последовательности – и существенная экономия времени. Поэтому описанный алгоритм так и назвали – быстрое преобразование Фурье.
Источники информации:
- Лаврус В.С. Практика измерений в телевизионной технике. – К.: НиТ, 1996.
- Карташкин А. Уйти, чтобы вернуться.
Дата публикации: 25 июля 2000 года