"DYNAMIC MODELLING AND SELECTION OF RATIONAL PARAMETERS OF COMPLEX MECHANICAL SYSTEMS BY EMPLOYMENT OF NATURAL FORMS "

Soliterman Y.L.,Goman A.M.,Alexandrova V.S.

(INDMASH NAHB, Minsk,Belarus)

The proposed methods of dynamic modelling of complex mechanical systems give the possibility to select the rational parameters of systems without performing troublesome calculations. Decomposition of motion on natural form consists of the base of such methods. These methods have received the practical employment in design tractor transmissions.

The mechanical drives are ones from the most responsible parts of the modern technical systems, which quite often limit their reliability, qualitative, and service characteristics. The dynamic loads and vibration which arise during their work promote to the nucleation and development of fatigue failures of high loaded elements of such drives, gradual reducing of resource and sometimes to abnormal failure of the whole drive. On this reason it seems essential during design of drive mechanism to perform rational selection and sometimes to provide the possibility of the control of dynamic system parameters with aim to lowering the intensity of oscillating processes in drive's units. The methods of rational design of dynamic system are based on employment of phenomenon that during resonance regimes the amplitude of forced oscillation is proportional to amplitude of appropriate natural forms. The suggested criteria of comparison for the competitive variants of dynamic system design are based on the analysis of natural oscillation forms and give the possibility to define the rational parameters of drives parts. On our opinion, the most effective method of analytical investigation of mechanical drive dynamic models is the decomposition of system's motion by natural forms. The motion of any system s element under the influence of disturbing variable forces is defined by expression:

       

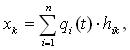
where q _i (t) - a normal coordinate; h _ik - an amplitude of oscillation of k mass on natural i form.

The rationalisation of drive may be achieved by variations of the system parameters (masses and rigidities). The analysis of the oscillation forms gives the possibility to find the most effective variant of system design. The level of minimum vibroactivity may be selected as a performance criterion and the rational parameters of the system may be defined at its base. For achieving this in the most of instances it is sufficient to limit consideration and analysis the first two or three oscillating forms only, because they have usually the primary influence. The dynamic system subjected to continuos spectrum G of disturbing oscillations is forced to fluctuate on natural frequencies located in this spectrum, li is supposed that the criterion of evaluation of vibroactivity for the possible competitive variants of dynamic system may be expressed through the norm amplitudes of natural forms:

       

where p ₁, p ₂ - spectra of frequencies of the competitive variants; h _ij, h _kj - norm natural forms of j structure; H _j - the degree of lowering of vibroactivity for j structure.

In machine's drives spectra of disturbing frequencies are usually located in some limited zone. So, for the selection of rational variant of dynamic system according to criterion (2) it is sufficient to limit the consideration of natural forms, the frequencies of which is located directly in this zone or close to it. This method gives the possibility on the design stage to perform the analysis and comparison of dynamic characteristics of complex systems without calculation of forced oscillation characteristics. In the case if the dynamic model is known and load factors may be defined, the ratio of vibroacceleration of system's elements may be used as a criterion of evaluation for the competitive variants of dynamic system. These vibroaccelerations are calculated by integration of differential equations of system's motion. This criterion is expressed as:

       

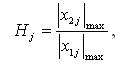
where x _1j, x _2j - vibroacceleralions of competitive variants for j element.

Let us consider the real application of above described method of investigation of dynamic loading in mechanical drives for the comparison of dynamic characteristics gearing with solid and self-adjusted gear wheels. Dynamic loading in gearing may be defined on the base of impact theory in proposition that the contact of conjugate teeth begins at velocity of impact . Dynamic model of gearing with solid wheels may be represented as chain two-mass system, and for self-adjusted wheels - chain three-mass system. The solution of these problems is defined by integration of differential equation systems at defined initial conditions with help of natural forms. The criteria of vibroactivity for considering variants of gearing may be expressed as and H2 for pinion and wheel correspondingly:

       

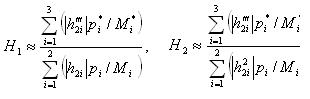
where p ₁, p ₂ - natural frequencies for gearing with solid wheels; p ₁*, p ₂*, p ₃* - natural frequencies for gearing with self-adjusted wheels; h ₂₁,h ₂₂ - amplitude values of wheel oscillations natural forms for gearing with solid wheels; h ₂₁", h ₂₂", h ₂₃" - amplitude values of wheel hub oscillations natural forms for gearing with self-adjusted wheels; M ₁, M ₂ - generalised masses for gearing with solid wheels; M ₁^*, M ₂^*, M ₃^* - generalised masses for gearing with self-adjusted wheels.

From (4) it is obvious, that effect of vibroactivity lowering is defined by natural forms and depends from their parameters only. The most rational design of gearing may be received by varying the parameters of dynamic system, such as, for example, mass of teeth ring and rigidity of elastic connection of ring and hub.

---

НАЗАД В БИБЛИОТЕКУ

---