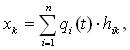
где q i (t) - нормальная координата; h ik - амплитуда колебания массы k на i-ой естественной форме.
Рационализация двигателя может быть достигнута изменениями параметров системы (массы и жесткости). Анализ форм колебания дает возможность найти наиболее эффективный вариант системы. Уровень минимума виброактивности может быть отобран как критерий выполнения, и рациональные параметры системы могут быть определены в ее основе. Для достижения этого в большинстве случаев достаточно ограничится рассмотрением и анализом первых двух или трех колебаний, потому что они имеют, как правило первичное влияние. Динамическая система, подвергнутая постоянному спектру G тревожащих колебаний вынуждена колебаться на естественных частотах, расположенных в этом спектре. Предполагается, что критерий оценки виброактивности для возможных конкурентоспособных вариантов динамической системы может быть выражен через амплитуды нормы естественных форм:

где p 1, p 2 - спектры частот конкурентоспособных вариантов; h ij, h kj - норма естественной формы j-ой структуры; H j - степень понижения виброактивности для j-ой структуры.
В спектрах двигателей машин волновые частоты обычно располагаются в некоторой ограниченной зоне. Так, для выбора рационального варианта динамической системы согласно критерию (2) достаточно ограничить рассмотрение естественных форм, частоты которых расположены непосредственно в этой зоне или близко к этому. Этот метод дает возможность на стадии проекта произвести анализ и сравнение динамических характеристик сложных систем без вычисления принудительных характеристик колебания. В случае, если динамическая модель известна и факторы груза могут быть определены, отношение виброускорений элементов системы может использоваться как критерий оценки для конкурентоспособных вариантов динамической системы. Эти виброускорения получены интегрированием дифференциального уравнения движения системы. Этот критерий имеет вид: :
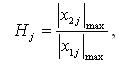
где x 1j, x 2j - виброускорения конкурентоспособных вариантов для j-го элемента.
Давайте рассмотрим реальное применение вышеупомянутого описанного метода исследования динамической погрузки в механических двигателях для сравнения динамических характеристик зацепления с твердыми и само - отрегулированными колесами механизма. Динамическая погрузка в зацеплении может быть определена на основе теории воздействия в суждении, что контакт сопряженных зубьев начинается на скорости воздействия . Динамическая модель зацепления с твердыми колесами может быть представлена как система двух- массовой цепи, и для само -отрегулированных колес - система трех- массовой цепи. Решение этих проблем возможно интегрированием дифференциальных систем уравнения при определенных начальных условиях с помощью естественных форм. Критерии виброактивности для рассмотренных вариантов зацепления могут быть выражены через и для связи и колесо соответственно:
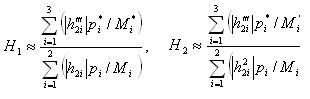
где p 1, p 2 - естественные частоты для зацепления с твердыми колесами; p 1*, p 2*, p 3* - естественные частоты для зацепления с само - отрегулированными колесами; h 21,h 22 - амплитуды колебаний колеса естественной формы для зацепления с твердыми колесами; h 21", h 22", h 23" - амплитуды колебаний центра колеса естественной формы для зацепления с само -отрегулированными колесами; M 1, M 2 - обобщенные массы для зацепления с твердыми колесами; M 1*, M 2*, M 3* - обобщенные массы для зацепления с само -отрегулированными колесами.
Из (4) видно, что эффект понижения виброактивности определен естественными формами и зависит только от их параметров. Наиболее рациональное зацепление может быть получено, изменением параметров динамической системы, её типа, например, массы зубчатого венца и жесткости упругой связи венца и центра. .
НАЗАД В БИБЛИОТЕКУ