Механическая обработка зубчатых колес на базе технологии непрерывного действия

Новикова О.Н., Горобец И.А., Сергиенко Д.К.(ДонГТУ, г. Донецк, Украина)

Оптимизация линии зацепления колесно-реечнои передачи при многопарном зацеплении /Прогрессивные технологии и системы машиностроения. Международный сб. научных трудов.– Донецк:ДонГТУ, 2001. Вып. 16. – c.139-145 .

Колесно-реечные движители, позволяющие преобразовать вращательное движение в поступательное и наоборот, нашли широкое применение в качестве исполнительных механизмов различных машин и установок.

Одним из основных требований к таким движителям является надежность их работы, высокий КПД, небольшая стоимость изготовления.

В результате проведенных нами экспериментальных исследований, установлено что процесс зацепления зубьев колесно-реечных движителей характеризуется зоной однопарного и двухпарного зацепления, причем зона двухпарного зацепления находится в пределах 5... 10% зоны однопарного зацепления.

Однако, незначительная по продолжительности зона двухпарного зацепления характеризует значительные изменения силовых и кинематических характеристик движителя, его КПД. Поэтому, при определении оптимальной линии зацепления необходимо учитывать не только зону однопарного, но и двухпарного зацепления.

В работе [2] авторами была получена энергетически оптимальная линия зацепления зубьев колесно-реечной передачи для зоны однопарного зацепления и определен оптимальный профиль зубьев колесно-реечного движителя с точки зрения минимизации скорости скольжения, а следовательно, минимизации работы трения.

В данной работе, как и [2], примем следующие допущения: потери Мощности от перекатывания профилей зубьев передачи пренебрежимо малы, по сравнению с потерями при скольжении; коэффициент трения скольжения мало зависит от скорости скольжения и равен 0,3; податливость зубьев элементов движителей не значима; флуктуации момента, реализуемого зубчатым колесом, отсутствуют; поле допуска межцентрового расстояния aw шага зубьев рейки РР) возникающая в процессе изготовления и эксплуатации, находятся в пределах 3% от номинальной их величины.

Здесь рассмотрим случай двухларного зацепления. Обозначим крутящий момент, приходящийся на любую i-тую точку контакта колеса через Ti. Тогда общий крутящий момент на колесе

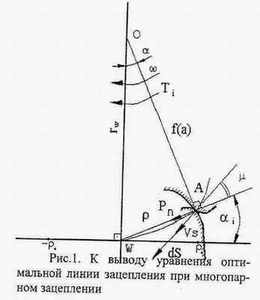
Тогда нормальная сила Рn в точках контакта, рис. 1

где rw - радиус начальной окружности колеса; а, - полярный угол i-той точки контакта оптимальной линии зацепления при многопарном зацеплении.

Будем считать процесс изнашивания установившимся, поэтому используем здесь линейные закономерности изнашивания материалов, установленные М.М. Хрущевым, Хирстом В. [1] в виде:

где Yn – скорость изнашивания по нормали к поверхности зубьев;

k = kу + k2 - коэффициент изнашивания, являющийся суммой коэффициентов изнашивания материалов в данных условиях:

Vi – скорость скольжения зубьев внешнего зацепления в точке i с координатой Pj (полярный радиус);

р - нормальное контактное давление в г-той точке;

w - угловая скорость колеса.

Принимаем, что в режиме установившегося изнашивания с учетом упругих деформаций условия неразрывности при изнашивании для чего, если крутящий момент не изменяется, сводится к равенству угловых скоростей изнашивания для любой i-той точки, т.е.

rw cosaj в (5) выражение (3), (4), (2) получим:

где w - угловая скорость изнашивания, приведенная к колесу.

Поскольку каждая контактная точка будет совершать один и тот же путь по линии зацепления при тех же условиях пересопряжения зубьев, то вычисления работы трения АТР (критерий оптимизации) приведет к одинаковым ее значениям для любой из них. Из выражения (6) выразим Тi:

Тогда мощность трения Niтр определяется как

Подставив в (8) выражение (7), получим;

Элементарная работа силы трения:

Исходя из данных [2] запишем выражение для dt:

где м- это угол между радиус-вектором р и касательной к линии зацепления, (см. рис. 1). Подставив в (10) зависимости (9) и (11), будем иметь:

Тогда полную работу сил трения найдем интегрированием вдоль участка Оцепления:

При решении задачи о минимуме работы трения, а следовательно и скорости изнашивания зубьев при двухпарном зацеплении, составим уравнение равновесия моментов всех сил, действующих в зацеплении. Поскольку силы в данном случае сосредоточены, то для нахождения их общего момента относительно оси колеса воспользуемся интегралом Стильтьеса. Но нормальные силы в точках контакта – непрерывные функции координат линии зацепления:

Линию зацепления разобьем на участки однопарного и двухпарного зацеплений. Примем, что участок однопарного зацепления соответствует углам (ao,ai), а один из участков двухпарного зацепления - углам (a1 ,а2 )При этом сосредоточенную функцию силы Р„ = Ф(а) будем считать интегрирующей функцией, а ее переменное плечо относительно центра колеса f(a) = rw cos a - интегрируемой функцией. Следуя правилу составления интеграла Стильтьеса:

Тогда, отбрасывая индексы i, получим:

Но

Где dP - элементарная сосредоточенная сила

рn – распределенная сила

Тогда, с учетом (17) имеем:

Значит выражение (19) можно получить с помощью вариационной техники по Эйлеру. Для этого постоянные члены вынесем за знак интеграла: