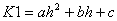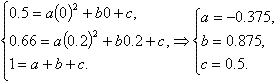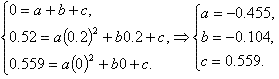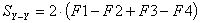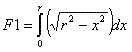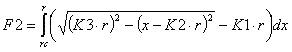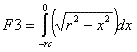Rus
L'exposé préparé pour l'intervention sur la chaire
CPM pour le jour de la science. (12.05.05)
La définition de l'aire de la section transversal du foret
Fedossov Nikolas
Le problème de la précision des trous reçu par les outils axiaux
coupant (foret) est actuel. Parfois à la projection de l'outil il est nécessaire de
calculer la valeur de l'erreur possible provoquées par lui pendant le travail. Par exemple,
calculer le foret pour la stabilité et la solidité. Il y a une multitude de
recommandations pour l'exécution de tels comptes. Mais ces recommandations concernent les
forets standard normalisés. Il y a une question : «Mais que faire, s'il y a des forets
distinguant de standard ?»
Au calcul des forets pour la solidité et la stabilité il est nécessaire de
savoir l'aire de la section transversal du foret. Le but du travail donné est généraliser
et déduire les dépendances de la géométrie de la section transversal du foret.
On livrait la tache tous les éléments géométriques de la section transversal
du foret lier au rayon du foret r et le rayon du coeur du foret rc,
qui se trouve en fonction de r, et est défini selon l'expression suivant:
rc= h•r,
Où h – le coefficient du rayon du coeur, pour les forets standard spiraux h = 0.12 – 0.25.
Nous trouverons la corrélation entre la valeur et la disposition de la rainure du copeau du foret (fig. 1).
Selon les recommandations [1, p.625] (voir fig. 2) au rayon du coeur rc = 0,2•r
le rayon de la circonférence de la rainure B=0.26D=0.52r. Le centre de
la circonférence donnée est déplacé en ce qui concerne le centre du foret sur
А=0.33D=0.66r selon l'axe Y – Y et sur С=0.1D=0.2r selon l'axe X - X.
Nous ferons les suppositions suivant:
- le coefficient du rayon du coeur h = 0 – 1,
- si h = 0: А=0.5r, С=0.25r,
- si h = 1: А=r, С=0, B=0,
- les valeurs А et B changent en fonction de la valeur du rayon du coeur selon
la loi quadratique, mais la valeur С selon linéaire.
Alors en prenant en considération les suppositions ci-dessus citées et nous
trouverons fig. 2 la corrélation entre le coefficient du rayon du coeur et А,
С, B.
Admettons que А=К1•r. Supposerons que:
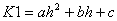
Trouverons les coefficients а, b et с.
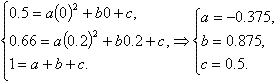
Alors
K1 = - 0.375h2 + 0.875h + 0.5
Analogiquement, admettons que B = К3 r. . Supposerons que:
K3 = a h2 + b h + c
Trouverons les coefficients а, b et с.
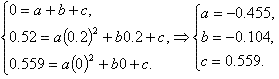
Alors
K3 = -0.455h2 - 0.104h + 0.559
Admettons que С = К2 r. Supposerons que:
K2 = a h + b
Alors, en prenant en considération plus haut dit, nous avons:
K2 = - 0.25h + 0.25
Ensuite trouverons l'aire de la section transversal du foret à l'aide de l'intégrale
définie. Définirons l'aire selon l'axe Y - Y (fig. 3) selon la dépendance suivant:
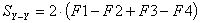
où
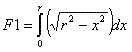
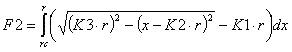
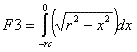
Présenterons les résultats des calculs pour le foret par le diamètre
5 – 20 mm sous forme du tableau 1.
| Le diamètre du foret, mm |
L'aire de la section transversal du foret, mm2 |
| rc / r |
| 0.1 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
| 5 |
9.099 |
9.54 |
11.499 |
15.279 |
18.115 |
19.625 |
| 10 |
36.396 |
38.161 |
45.996 |
61.118 |
72.462 |
78.5 |
| 20 |
145.584 |
152.642 |
183.984 |
244.472 |
289.847 |
314 |
Les dépendances déduites pour la définition de l'aire de la section
transversal du foret spiral ont l'erreur admise à la conception dans les industries
mécaniques et l'intervalle limitatif de l'utilisation :
0 < h < 1.
Список литературы: 1. Пономарев С.Д. Основы современных методов расчета на прочность в
машиностроении./М: Машгиз, 1952. – 864с.