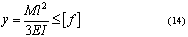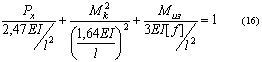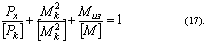Машиностроение и техносфера ХХІ века // Сборник трудов межд. н/т
конференции в г. Севастополе 13 – 18 сентября 2004 г. В 4-х томах. - Донецк: ДонНТУ, 2004. Т2.
С. 194 - 196.
УСТОЙЧИВОСТЬ ОДНОСТУПЕНЧАТОГО ОСЕВОГО ИНСТРУМЕНТА
Малышко И.А., Коваленко В.И., Кизименко Т.М.
(каф.ТМ, ДонНТУ, г. Донецк, Украина)
Осевой инструмент представляет собой упругую систему с различными сочетаниями
не только составляющих усилий резания на каждой ступени, но и систему взаимосвязи между силами,
действующими на каждую ступень.
Поэтому осевой инструмент можно представить как упругую систему с многопараметрическими
воздействиями.
При проектировании нового инструмента или при наличии готового инструмента возникает
необходимость, в определении допустимой величины подачи исходя из устойчивости инструмента,
особенно, когда l/d>10-20.
Устойчивость прямолинейного стержня, находящегося под действием приложенных к его концам
сжимающих сил и скручивающих моментов характерного, например, для одномерного инструмента при
отсутствии радиальных неуравновешенных сил была рассмотрена А.Г.Гринхиллом. Предполагая, что
концы стержня оперты, а главные жесткости его равны, он установил, что критическая длина
стержня l, за которой его прямолинейная форма теряет устойчивость, определяется:
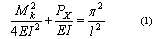
где Mk - крутящий момент действующий на стержень; Px - осевая
сила; E - модуль упругости материала стержня; I - осевой момент инерции; l - длина
стержня.
Исследования устойчивости стержня опертого обеими концами, когда его главные жёсткости не
равны, были проведены Грамелем, который установил, что:
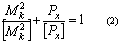
где Mk - крутящий момент, прикладываемый к упругой системе; [Mk] -
критический крутящий момент при чистом изгибе; Px - осевая сжимающая сила;
[Px] - значение критической осевой силы при чистом изгибе.
При совместном действии осевой и поперечной сил величина наибольшего изгибающего момента
определяется зависимостью:
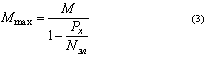
M - изгибающий момент от поперечной нагрузки; Nэл - величина
Эйлировой силы.
Устойчивость инструмента, работающего по последовательной схеме резания, нагруженного
осевой силой Px , крутящим моментом Mk, и изгибающим моментом
от неуравновешенной радиальной силы Mиз, можно выразить с учётом следующих
уравнений энергетическим критерием устойчивости:
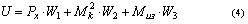
где U - энергия деформации упругой системы; W - работа внешних сил;
W1, W2, W3 - геометрические характеристики,
являющиеся квадратическими функциями потери устойчивости.
Полагая, что M2x = Pэк уравнение можно
представить в виде:
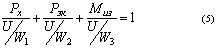
Данное уравнение является уравнением устойчивости или уравнением безопасности при
трёхпараметрическом нагружении по координатам XYZ для одномерного инструмента.
Критическое значение осевой нагрузки, при котором прямолинейная форма равновесия переходит
из устойчивого состояния в неустойчивое, определяется из равенства:
U = W . (6)
Учитывая, что 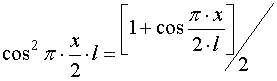 уравнение можно привести к виду:
уравнение можно привести к виду:
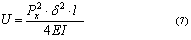
Тогда, подставив значение U в уравнение работы, произведённой осевой силой
Px, при изгибе оси инструмента получим:
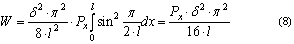
После подстановки значений [6] и [7] в равенство [5] и соответствующих преобразований
получим уравнение критической осевой силы для одномерного инструмента:

Путём дальнейших преобразований получаем, что:
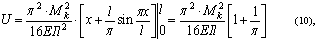
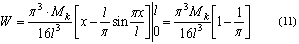
Критическое значение крутящего момента, при котором прямолинейная форма равновесия переходит
из устойчивого состояния в неустойчивое, определится из равенства [5].После подстановки значений
уравнений [9] и [10] получим:

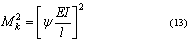
где 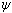 = 1.64 - коэффициент устойчивости.
Третьим членом уравнения устойчивости является отношение изгибающих моментов,
создаваемых радиальной неуравновешенной силой Py, к изгибающему моменту,
допускаемому стержнем. Критерием допускаемого изгибающего момента могут быть напряжения,
допускаемые стержнем при изгибе или величина прогиба. На данном этапе исследований допускаемый
изгибающий момент будет определяться через допускаемую величину прогиба, которая при консольном
закреплении стержня определяется зависимостью:
= 1.64 - коэффициент устойчивости.
Третьим членом уравнения устойчивости является отношение изгибающих моментов,
создаваемых радиальной неуравновешенной силой Py, к изгибающему моменту,
допускаемому стержнем. Критерием допускаемого изгибающего момента могут быть напряжения,
допускаемые стержнем при изгибе или величина прогиба. На данном этапе исследований допускаемый
изгибающий момент будет определяться через допускаемую величину прогиба, которая при консольном
закреплении стержня определяется зависимостью:
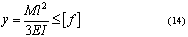
[ f ] - допускаемая величина прогиба инструмента.
Принимая, что y = [ f ] значение допускаемого изгибающего момента определится
из уравнения [13] зависимостью:

Пространственное уравнение устойчивости [5] после подстановки критических значений нагрузок
Pk, Mk, [ M ] будет иметь вид:
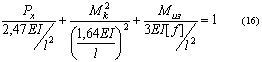
В общем виде уравнение устойчивости можно записать:
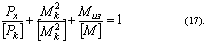
В результате исследований была составлена таблица влияния составляющих силы резания на
устойчивость инструмента, в зависимости от его длины, при t = 2,5мм; S = 0,4мм/об; d = 20мм.
Таблица 1.- Влияние составляющих сил резания (Px,
Py, Mk) на устойчивость зенкеров, в %
| L, мм |
Px |
Py |
Mk |
| 60 |
1.27 |
98.7 |
0.03 |
| 400 |
17.14 |
82.7 |
0.1 |
| 800 |
44.28 |
55.5 |
0.22 |
Из таблицы видно, что преобладающее влияние на устойчивость инструмента оказывают радиальные
неуравновешенные силы. По мере увеличения длины инструмента, при постоянном диаметре, от 60 мм
до 800 мм степень влияния радиальных неуравновешенных сил на устойчивость инструмента уменьшается,
а осевых сил увеличивается.
Крутящий момент на устойчивость инструмента не оказывает существенного влияния. Но с
увеличением длины рабочей части инструмента в 2,8 раза степень влияния крутящего момента
увеличивается в 7,3 раза. Поэтому при сверлении сверхглубоких отверстий, у которых l/d>20,
влияние крутящего момента на устойчивость необходимо учитывать.
Список литературы: 1. Малышко И.А. Основы теории проектирования осевых
комбинированных инструментов, Автореферат докторской диссертации/ДонГТУ.-Донецк,1995.-36с.
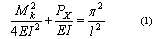
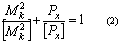
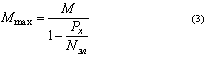
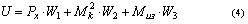
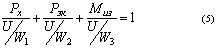
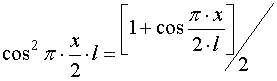 уравнение можно привести к виду:
уравнение можно привести к виду:
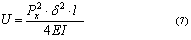
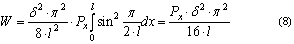

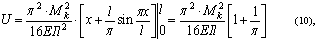
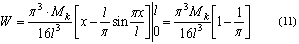

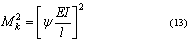
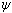 = 1.64 - коэффициент устойчивости.
= 1.64 - коэффициент устойчивости.