К ВОПРОСУ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СМЕШАННЫХ ГРАНИЧНЫХ УСЛОВИЙ В КРАЕВЫХ ЗАДАЧАХ ТЕОРИИ ОБОЛОЧЕК И ПЛАСТИН
http://www.rusnauka.com
Пасечник В.А.
Днепропетровский национальный университет
Решение многих практических задач расчета современных конструкций на базе оболочек и пластин связано с необходимостью математического описания сложных условий закрепления их контура. Основными широко используемыми и хорошо изученными моделями в этих задачах являются, ставшие уже классическими, граничные условия шарнирного опирания и жесткого защемления контура.
В настоящей работе для описания сложных условий закрепления оболочек и пластин предложены математические модели, позволяющие эффективно использовать методы возмущений для построения аналитических решений соответствующих краевых задач.
Так условия упругого закрепления контура пластины предлагается представить в виде комбинации граничных условий шарнирного опирания и жесткого защемления
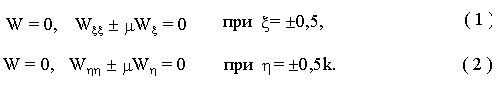 где эпсилон, этта - безразмерные координаты, мю - коэффициент упругого защемления.
где эпсилон, этта - безразмерные координаты, мю - коэффициент упругого защемления.
Коэффициент упругого защемления представляем в виде 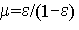 , тогда граничные условия (1), (2) запишутся в виде
, тогда граничные условия (1), (2) запишутся в виде
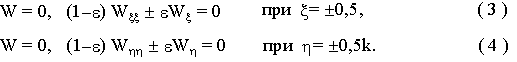
Для случая смешанных условий закрепления контура "шарнир - упругое защемление - жесткое защемление", соответствующие граничные условия предлагается представить следующими соотношениями
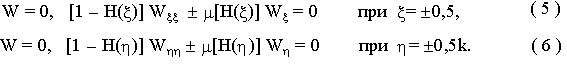
Здесь 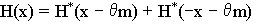 , H*(x) - функция Хевисайда, qm - величина участка шарнирного опирания.
, H*(x) - функция Хевисайда, qm - величина участка шарнирного опирания.
В предложенные соотношения граничных условий (3) - (6) входит малый параметр e, что дает возможность применить метод возмущения для построения асимптотического решения соответствующей краевой задачи [1].
Литератра:
1. Андрианов И.В., Пасечник В.А. Численно–асимптотический метод решения нелинейных смешанных краевых задач механики //Вісник Дніпр. у–ту. Механіка. –1999. –Вип.2. Т.2. –С.5–12.
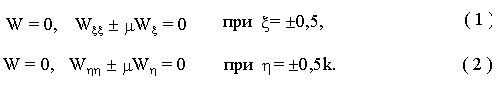 где эпсилон, этта - безразмерные координаты, мю - коэффициент упругого защемления.
где эпсилон, этта - безразмерные координаты, мю - коэффициент упругого защемления.
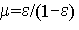 , тогда граничные условия (1), (2) запишутся в виде
, тогда граничные условия (1), (2) запишутся в виде
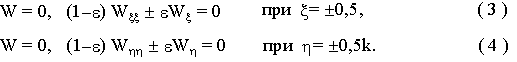
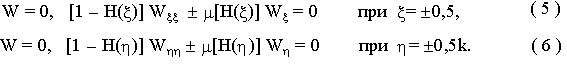
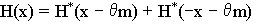 , H*(x) - функция Хевисайда, qm - величина участка шарнирного опирания.
, H*(x) - функция Хевисайда, qm - величина участка шарнирного опирания.