 (2)
(2)
1996 Canadian Conference on
Electrical and Computer
Engineering
Ìàó
26 - 29, 1996Sponsored by
IEEE Canada
CONFERENCE PROCEEDINGS
theme
Glimpse into the 21st Century
Edited by
Terrance J. Malkinson University of Calgary
VOLUME I
IOrganized with the participation of
The University of Calgary
Department of Electrical and
Computer Engineering
²55Í
Electromagnetic compatibility in electric circuits: a modelling approach
Eduard G. Kurennyi and Elena N. Dmitrieva
^ Donetsk State University, Artyoma Street, 58
Donetsk 340000, Ukraine
* Stockholding Company “Concern STIROL"
Gorlovskaia Divizia Street, 10
Gorlovka 338010, Ukraine
Problem description
Conventional indices of electromagnetic compatibility (EMC) are valid, as a rule, for the particular type of interference, e.g. stationary or periodic. However, the problem of estimation of voltage oscillations revealed that these were insufficient and inaccurate. It was proposed to base the indices on models of the influence of illumination oscillations on people [1,2]. We think that other EMC indices in the 21st century will be developed similarly. In this work we provide examples to show the effectiveness of such an approach.
Modelling principles
Since electrical systems are affected by the consequences of EMC distortions rather than the interference parameters, evaluation of EMC should be based on models of interference influences on electrical systems, circuits and people. A model of the object should be simple enough for practical applications, while possessing the principal properties of the object such as its
reaction, y(t), to an interference, un(t), and the inertia. The model should include the following modules: (1) the module for extraction of the interference from the input process u(t), (2) the filter that models the reaction, (3) the module that squares the object reaction (the influence of the interference depends on the power of the object reaction), and (4) the module for modelling the inertia. Since the process on the output of the module 3 reflects directly or indirectly the EMC distortions, the changes in its amplitude are the current values of the dynamic EMC index.
The inertia of the object with the inertial constant T can be easily modelled using the inertial smoothing:
T Y /T(t)+ Y T(t)=y2(t) (1)
or the sliding averaging (averaging on an interval):
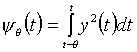 (2)
(2)
on the period q (Dirichlet window). The functions Y T and Y q will be referred to as the inertial dose and cumulative dose, respectively.
If changes in the interference are small then the filter (module 2) can be linearized. If the average reaction is big then module 3 may be omitted.
Standards, measurements, and calculations
EMC standards should be established on the basis of the acceptability of the object reaction to an interference. This is usually applied to simple
types of interference, such as constant, when knowing amplitude of the interference is sufficient, or periodic, when knowing the frequency is also necessary. However, this inevitably raises the problem of equalizing of complex and simple types of interference. Obviously, it is impossible to do without using an EMC model. The standard dynamic index (standard dose, Y ) is defined for both simple and complex types of interference. Thus, a modelling approach allows generalization of currently used standards to any type of interference.
Unambiguous, accurate and significant EMC estimates are achieved when a structural EMC scheme (as in [1]) is standardized, and the measuring devices have the same structure as the model. Currently used standards for EMC indices are employed for calibration. In spite of the complexity of the devices, EMC estimates become simple since the index value is observed directly. It is necessary to standardize the requirements to the accuracy of reproduction of the frequency functions and the transfer functions of the model modules.
The dynamic indices for one source of interference is to be estimated empirically or theoretically. The index for a set of sources of interference can then be derived using methods of probability theory. The usage of dynamic indices can simplify calculations.
Voltage asymmetry
!
The voltage asymmetry causes additional heating of electrical systems. Currently used standards limit the coefficient of asymmetry, K2,(the relative value of the reversed sequence voltage U2) and the period of time, q 2, when it exceeds the limit K2 are standardized [3]. These indices are only correct for slowly changing interference, when the duration of the interference is longer than the standard Q2.
In order to generalize the currently used standards to any type of interference it is worthwhile to use the dynamic index, the cumulative coefficient of asymmetry k2q . The corresponding model consists of two modules: module 1 extracts the acting values U2 from the voltage u(t), while module 4 performs the cumulative transformation (2) of the process U2(t) on the interval q 2. The acceptable limit k2q is equal to K2.
The nature of the problem dictates that another model may be used which would include module 3 and module 4 of inertial smoothing (1) at T2=q 2/3. The inertial dose Y T2 in relative units corresponds to temperature.
Using the doses it is possible to minimize the requirements to EMC, and hence to minimize extra cost of EMC stabilization. Without considering the inertia of the object, the asymmetry should be estimated on the basis of maximum current value, K2max. Due to smoothing (1) or averaging (2), the maximum dose value is smaller than K2max.
Non-sinusoid voltage
Conventional EMC indices are mainly related to particular cases of periodic interference or failures in sinusoid shape. We introduce a system of more general indices:
- the tnertial coefficient of non-sinusoid shape reflecting additional heating of objects with active conductance;
- the dynamic coefficient of non-sinusoid shape reflecting additional heating of objects with capacitive conductance (capacitors, insulation etc.);
- the coefficients of narrow-band nitration modelling interference influences on objects that are sensitive to narrow-band interference close to harmonic frequencies;
- the dose of non-sinusoid shape estimating energy of deflection from a sinusoid shape over a particular period of time (e.g. trigger pulse duration).
In contrast to the conventional indices, ours are invariant to the kind of interference and include inertia of objects.
The model for active conductance has only module 1 of extraction of distortions from a sinusoid, module 3 and module 4 of cumulative averaging. The standard for the inertial coefficient of non-sinusoid shape is equal to the coefficient of non-sinusoid shape calculated from acting voltage values of harmonics.
The model for capacitive conductance should also include module 2 which models the current in a real capacitor. The standard for the dynamic coefficient of non-sinusoid shape is established from the acceptable overloading of the capacitor during a particular period of time, e.g. 30% during 3-5 min. In case of periodic interference with v-harmonics of amplitude UV, this condition can be expressed in relative units as:
![]() (3)
(3)
This gives the value for a dynamic coefficient of non-sinusoid
shape: ![]()
Voltage oscillations
The oscillations in illumination cause additional fatigue in people, which decreases their productivity and may lead to the health problems. Therefore, the dynamic model (flickermeter) is to model a fatigue. The model described in [1] complies with such a criterion reasonably well. Its disadvantage is that the band-pass characteristics of the filter does not correspond to experimental data at low frequencies. In order to avoid underestimation of the requirements at frequencies Í 0.5 Hz, the fixed value for the voltage oscillations is used (0.514% in Table II).
We think that the reason for this is lack of consideration of slow vision adaptations. We have proposed to include into the flickermeter a module of slow adaptation, which is a real differential unit with the gain 0.09 and the time constant 70 s [3]. This additional module removes the disadvantage mentioned above.
In addition, on the basis of experiments performed together with V.M. Kovalchuk, we propose to estimate the fatigue using transformation (2) at q =10 min, as in [4]. This allows the simplification of modules 4 and 5 in [1] ;
and the summation of flicker doses from several sources of interference.
The experiments on the estimation of duration of cumulative fatigue were performed as follows. A volunteer was asked to read a text placed in the frame, which was connected to a movement detector. The volunteer's head was fixed so that
the volunteer had to adjust position of the frame m order to achieve better vision conditions. The volunteer was unaware when the voltage oscillations were applied to the lamp. The initial parts of the graph of the frame movement were similar with and without the oscillations. However, in 8-10 mm after the oscillations had been applied the amplitude of the frame movements significantly increased.
The standardization based only on the magnitude and frequency of the oscillations gives different results for the interference of different nature (e.g. rectangular pulses vs. sinusoid) or even for the interference of the same nature but of different proportions (e.g. rectangular pulses of different durations occurred at the same frequency). The error in EMC estimation comparing to the flicker dose may be substantial. For example, the method in [4] overestimates the EMC requirements by 3.8-4.7 fold for the group of rolling mills.
Conclusions
1. Most existing EMC indices are valid and | provide unambiguous, accurate and significant f EMC estimates only for particular cases of stationary or periodic interference.
2. Objective EMC indices are established on the oasis of modelling interference influences on electrical systems, circuits and people. For practical purposes, structural EMC models should be designed as a linear block modelling the object reaction on interference and a non-linear block Evaluating consequences of EMC distortions.
3. Consideration of the inertia of the object
avoids overestimates of the requirements for EMC, which is especially significant for countries with limited energy resources.
4. New generation devices for EMC evaluation must have the same structural scheme as the corresponding EMC model. This makes them universal and profoundly simplifies measurements in electrical circuits.
Acknowledgements
We gratefully acknowledge the contribution of Dr. V.M. Kovalchuk to the conduct of the experiments on visual fatigue. We also thank Dr. D.E. Kurennyi for the help in the manuscript preparation.
References
[1] Flickermeter: Functional and design specifications. Report of International Electrotechnical Commission, vol. 868,1986, p.31. [2] A.K. Shidlovskii and E.G. Kurennyi, Introduction to the statistical dynamics of electrical systems, Kiev: Naukova Dumka, 1984 (in Russian). [3] Planning limits for voltage Unbalance in the United Kingdom. The Electricity Council, Engineering Recommendation, London, 1978, p.29. [4] GOST 13109-87. Electrical Energy. Requirements to the quality of electrical energy in electrical circuits of general usage. Started 1 January 1989 (in Russian).