LINEAR FILTRATION OF RANDOM PROCESSES IN EMC MODELS:
THE "PARTIAL REACTION" METHOD
Eduard G. Kourennyi*, Victor A. Petrosov**, Lidiya V. Chemikova*
Fifteenth International Wroclaw symposium and exhibition: Electromagnetic compatibility 2000.- Wroclaw: National Institute of Telecommunications, 2000, part 2.- P. 587-590.
*ChairofEPG, The Donetsk State Technical University, Artema St.,
58, Donetsk 83000 Ukraine,
led@gdgru.doneisk.ua,
lida@elf.donntu.ru
**ChairofEPP, The Priasovsk State Technical
University, Republic alley, 7, Mariupol
87500,Ukraine
The task of determination of random process characteristics on linear filter output is considered and unified calculation method is suggested. It is based on representation of linear system inform of linear aperiodic links connected in parallel. This method allows to umfv and simplify solution of linear filtering problem. The effectiveness of method is illustrated by EMC estimation of lighting facilities by dose of voltage oscillations.
1. PROBLEM DESCRIPTION
Linear filter is a component in the dynamic EMC model. The filter models the reaction Y(t) of an object to the interference X(t). The problem consists of the determination of probabilistic reaction characteristics from the known interference characteristics. Generally, this problem is solved within the bounds of correlation theory of random processes. For simplicity, let us limit the problem to finding the reaction dispersion DY(t) from the influence of stationary random interference on an object. We assume that the con-elation function KX(t ) and the spectral density SX(w ) do not depend on time t.
After feeding stationary interference to the object input, the transitional random process starts to proceed at the object output, and for t® ¥ the steady state sets in. For the steady state, the reaction dispersion can be calculated by well-known formulas (e.g. [1]):
![]() (1)
(1)
where g(t) is the weight or impulse function of the filter, A(w ) is the amplitude-frequency function of the filter, and v and u are variables of integration.
The usage of these formulas, however, entails cumbersome computations. First, the filter should be described by linear differential equation of the nth degree (n is high), making the expression for g(t) and A(w ) quite complicated. For example, for the flickermeter filter n=4 [2]. Second, it is necessary to fulfil double integration in each new task.
The purpose of the paper is to work out a unified calculation method that would allow solution of the problem by algebraic transformation without integration. There are two types of the problem: in the first type the unification is realized partially for every type of the interference correlation function; in the second type the total unification is realized.
2. PROBLEM OF THE FIRST TYPE
The idea of the suggested method is that the filter with
complex structure is represented in the form of linear aperiodic links connected
in parallel.![]()
The decision reaction equals to the sum of "partial" reactions y(t) of each link to interference. Transfer coefficients a and time constants J of the links are determined from the condition that the transfer function G(s) of the filter must be equal to the sum of transfer functions of the links.
The transfer function of the filter is equal to the ratio of two polynomials/^-) and z(s). This ratio is expressed by means of simple roots s1, s2, ...., sn of equation z(s)=0. This allows dcterm ination of characteristics of any link i:
 ;
Ji=-1/si , (2)
;
Ji=-1/si , (2)
where Tnn is the coefficient of sn in the polynomial
z(s). For s=si, the value of ai is not zero because the multiplier (s-si) is cancelled by the same multiplier in denominator. The values of link parameters can be complex, however the imaginary quantities are absent in final expressions.
The same process X(l) is fed to the inputs of links, thus the "partial" reactions are correlated variables. Therefore, in addition to "partial" dispersion Dy, it is necessary to take into account the intercorrelation moment kir. Intercorrelation moment between i and r "partial" reactions is calculated by formula
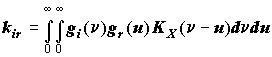 , (3)
, (3)
The decision dispersion of reaction is
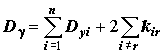 , (4)
, (4)
For each type of correlation function, Dy and kir were calculated by means of using g(t) =g ae-g t as weight functions in formulas (1) and (3), with g =1/T. For instance, for exponential correlation function with dispersion Dx and parameter a we will have
 ,
,
 ,
(5)
,
(5)
Correlation functions of reactions are found similarly.
Thus for users this task comes to determination of roots si and to algebraical calculations by formula (4). Unification of computations means that the same expressions for Dy and kir are used for filters of different structure.
In this case unification is not total because quantities Dy and kir are different for different correlation functions. However fundamental advantage of such unification is that it can also be applied to nonstation-ary processes X(t) and Y(t).
3. PROBLEM OF THE SECOND TYPE
Total unification of calculations is only possible for the steady state processes (indicated by tilde. ~). It is well known that stationary process X(t) is a result of passing white noise x (t) through a linear svstem with transfer function GX{s) (Fig 2), the parameters of which depend on interference correlation function tvpe. For example, for exponential correlation function the linear system is an aperiodic link with parameters
 ,
,
![]()
where the constant c is spectral density of white noise.
As a result, the filter can be represented as the combined system with transfer function Gc(s)=GX(s)G(s). If m is the degree of the polynomial in denominator G(s), then the system has n+m degree.
Instead of interference, white noise is fed to the input of the combined system. Using the "partial reactions" method for this system, one can obtain n+m linear aperiodic links connected in parallel. Parameters a and J of these links are determined by formulas (2), but for n+m roots. Spectral density of white noise is equal to the constant c and the correlation function of white noise is expressed through delta-function:
![]() , (7)
, (7)
Using these values in formulas (1) and (2) yields simple expressions after integration:
 ,
, 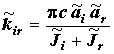 ,
(8)
,
(8)
Decision dispersion is calculated by formula (4). In the final expression, the constant quantity nc is canceled out. Therefore we can put nc=\. Unification of calculation is total since formulas (8) are independent on the type of correlation function and G(s).
5. CONCLUSION
It is recommended that determination of the process characteristics after linear filtering in EMC models is done using "partial reactions" method, which unifies and simplifies the calculations.
6. REFERENCES
6.1 A.K. Shidlovskyi, E.G. Kourennyi "Introduction in statistical dynamics of power supply systems" (in Russian), Naukova dumka, Kiev, 1984, pp. 56-57 .
6.2 "Flickermeter. Functional and design specifications" (in English), IEC, Publication 868, Geneva, 1986, p. 19.
6.3 COST 13109-87 "Electrical energy. Requirements for quality of electrical energy in general-purpose electrical networks" (in Russian), Moscow, brought to use at 01.01.89.pp.2-3.