Как известно, анализ динамических режимов выполняется как при проектировании, так и при эксплуатации электрических систем. Наиболее жесткие требования к методам оценки устойчивости возникают при решении задач противоаварийного оперативного управления. Анализ большого числа работ показывает, что методы анализа динамической устойчивости энергосистем могут быть разбиты на группы [1]: численные методы оценки устойчивости во временной области; прямые методы по типу метода Ляпунова и псевдометоды ляпуновских подходов. Эти исследования позволили сформулировать такие выводы [1]: проблему оценки области устойчивости можно решать, рассматривая одно- или двухмашинный эквивалент многомашинной энергосистемы; проблему моделирования можно решать путем интеграции прямого метода с расчетами процессов во временной области.

Сегодня более чем когда–либо разгосударствление электроэнергетики делает совершенно необходимым решение проблемы надежности режима по отношению к динамическим возмущениям для задач оперативного управления и планирования межсистемных обменов энергией во временном разрезе от одних суток до получаса [1]. В зависимости от того, каким образом получена информация о параметрах режима во времени (от программы расчета переходного процесса или от средств измерений параметров режима реальной системы в темпе прогресса), различают реализации гибридных программ в форме превентивного или противоаварийного SIME. Согласно [1] метод превентивный SIME в настоящее время состыкован с промышленными программами и проверен на многих моделях энергосистем ряда стран Европы, США, Канады и др. В этих работах используются классические модели синхронного генератора. Наиболее полная модель учитывает физические процессы в роторе генератора с помощью одного демпферного контура в осях d и q.

Таким образом, повышение эффективности функционирования гибридных методов может быть обеспечено достоверностью отражения физических процессов в синхронном генераторе при условии сохранения уровня сложности математической модели.

В данной работе излагаются результаты разработки методов анализа асинхронных режимов. Методы основаны на использовании математической модели генератора, которая при повышении точности описания физических процессов в генераторе по сравнению с классическими моделями генератора, используемыми в многомашинных моделях электрических систем, с точки зрения вычисления практически соответствует затратам при использовании классической модели.

Как известно, уравнения Парка–Горева в оперативной форме имеют вид:

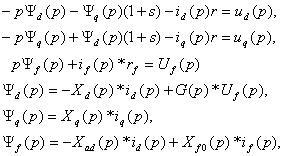
где Xd(p), Xq(p) – операторные сопротивления синхронного генератора по осям d и q ротора; Xf0(p) – операторное сопротивление со стороны обмотки возбуждения при разомкнутой обмотке статора; G(p) – операторная роторная проводимость генератора; S – скольжение ротора; id, iq, if – токи обмотки статора по осям симметрии ротора и возбуждения соответственно; r, rf – активные сопротивления обмоток статора и возбуждения.

Выполним следующие преобразования:

- определим токи по осям d, q при неучете активных сопротивлений и ЭДС трансформации;

- определим потокосцепления с учетом токов статора;

- определим на основании произведений токов и потокосцеплений мощности:

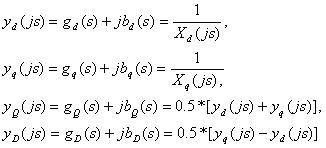
выражения для расчета активной и реактивной мощностей.

Выражение для расчета активной мощности состоит из следующих составляющих:

- первое слагаемое выражения это синхронная мощность;

- второе слагаемое включает в себя среднюю и пульсирующую составляющие асинхронной мощности и мощность динамической явнополюсности.

При неучете возбуждения получаем приведенные в [2] выражения для расчета асинхронного режима генератора при отсутствии возбуждения.

Зависимости G(js), gd(s), gq(s), bd(s), bq(s), gD(s), gQ(s), bD(s), bQ(s) могут быть определены через параметры многоконтурных схем замещения с вынесенным контуром намагничивания либо с учетом обмоток статора и возбуждения.

Система дополняется дифференциальными уравнениями, описывающими работу систем автоматического регулирования скорости агрегата и возбуждения генератора.

Анализ расчетов экстремальных значений скольжений в асинхронном режиме для различных генераторов при различном состоянии обмотки возбуждения при использовании типовых параметров демпферных контуров [3] позволяет сделать следующие выводы:

- изменение индуктивного сопротивления рассеяния влияет на экстремальное значение скольжения в большей степени, чем изменение сопротивления взаимоиндукции;

- индуктивное сопротивление рассеяния обмотки возбуждения при его изменении в пределах от минимального до максимального значений для конкретных генераторов, практически не сказывается на значении экстремума скольжения;

- значение активного сопротивления обмотки возбуждения значительно влияет на экстремальное значение скольжения.

Сопоставительный анализ результатов расчетов асинхронного режима при использовании полученных моделей генератора с результатами расчетов по полным уравнениям Парка - Горева и данными натурных экспериментов показал эффективность предложенных моделей. При достаточной точности определения режимных параметров по сравнению с классическими моделями требуются существенно меньшие затраты машинного времени по сравнению с вариантом использования уравнений Парка – Горева при использовании многоконтурных схем замещения.

ЛИТЕРАТУРА

1. Павелла М. Об общей теории Ляпунова к практическому прямому методу анализа динамической устойчивости // Электричество.2000. №6. С. 14-26.

2. Заболотный И.П., Диа Ибрагим. Разработка минимальной сложности математической модели генератора для анализа длительных переходных процессов в энергосистемах // Сборников научных трудов Донецкого государственного технического университета. Серия: электротехника и энергетика, выпуск 2 – Донецк: ДонГТУ. – 1998. – С. 181 – 188.

3. Лукашов Э.С., Калюжный А.Х., Гамм Б.З. Определение и использование в расчетах типовых характеристик и параметров демпферных контуров турбогенераторов // Электричество. 1997. №7. С.27-32.