 (2.1)
(2.1)
При анализе и оценке надежности, в том числе и в электроэнергетике, конкретные технические устройства именуются обобщенным понятием "объект". Объект - это предмет определенного целевого назначения, рассматриваемый в периоды проектирования, производства, эксплуатации, изучения, исследования и испытаний на надежность. Объектами могут быть системы и их элементы, в частности технические изделия, устройства, аппараты, приборы, их составные части, отдельные детали и т.д.
В соответствии с ГОСТ 27.002-89 "Надежность в технике. Основные понятия. Термины и определения" надежность трактуется как свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонта, хранения и транспортирования. Как видно из определения, надежность является комплексным свойством, которое в зависимости от назначения объекта и условий его пребывания может включать безотказность, долговечность, ремонтопригодность и сохраняемость или определенное сочетание этих свойств.
Безотказность - свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.
Долговечность - свойство объекта сохранять работоспособное состояние при установленной системе технического обслуживания и ремонта.
Ремонтопригодность - свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта.
Сохраняемость - свойство объекта сохранять в заданных пределах значения параметров, характеризующих способность объекта выполнять требуемые функции, в течение и после хранения и (или) транспортирования.
Указанные важнейшие свойства надежности характеризуют определенные технические состояния объекта. Различают пять основных видов технического состояния объектов.
Исправное состояние. Состояние объекта, при котором он соответствует всем требованиям нормативно-технической и (или) конструкторской (проектной) документации.
Неисправное состояние. Состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно-технической и (или) конструкторской (проектной) документации.
Работоспособное состояние. Состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской (проектной) документации.
Неработоспособное состояние. Состояние объекта, при котором значения хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям нормативно-технической и (или) конструкторской (проектной) документации.
Предельное состояние. Состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна , либо восстановление его работоспособного состояния невозможно или нецелесообразно.
Переход объекта (изделия) из одного вышестоящего технического состояния в нижестоящее обычно происходит вследствие событий: повреждений или отказов. Совокупность фактических состояний объекта, к примеру, электроустановки, и возникающих событий, способствующих переходу в новое состояние, охватывает так называемый жизненный цикл объекта, который протекает во времени и имеет определенные закономерности, изучаемые в теории надежности.
Согласно ГОСТ 27.002-89 отказ - это событие, заключающееся в нарушении работоспособного состояния объекта.
Повреждение - событие, заключающееся в нарушении исправного состояния объекта при сохранении работоспособного состояния.
Переход объекта из исправного состояния в неисправное не связан с отказом.
В ГОСТ 15467-79 введено еще одно понятие, отражающее состояние объекта - дефект. Дефектом называется каждое отдельное несоответствие объекта установленным нормам или требованиям. Дефект отражает состояние отличное от отказа. В соответствии с определением отказа, как события, заключающегося в нарушении работоспособности, предполагается, что до появления отказа объект был работоспособен. Отказ может быть следствием развития неустраненных повреждений или наличия дефектов: царапин; потертости изоляции; небольших деформаций.
В теории надежности, как правило, предполагается внезапный отказ, который характеризуется скачкообразным изменением значений одного или нескольких параметров объекта. На практике приходится анализировать и другие отказы, к примеру, ресурсный отказ, в результате которого объект приобретает предельное состояние, или эксплуатационный отказ, возникающий по причине, связанной с нарушением установленных правил или условий эксплуатации.
При расчетах и анализе надежности широко используются термины "элемент" и "система". Под элементом понимается часть сложного объекта, которая имеет самостоятельную характеристику надежности, используемую при расчетах и выполняющую определенную частную функцию в интересах сложного объекта, который по отношению к элементу представляет собой систему.
Например, изолятор в гирлянде изоляторов выполняет роль элемента, а гирлянда изоляторов - это система. На трансформаторной подстанции выключатели, отделители, разъединители, силовые трансформаторы и т.п. являются элементами, а сама подстанция является системой. Из приведенных примеров видно, что в зависимости от уровня решаемой задачи и степени объединения анализируемых аппаратов и устройств определенный объект может в одном случае быть системой, а в другом - элементом. Так при анализе надежности трансформатора его можно "разложить" на множество элементов: обмотки высокого и низшего напряжения, высоковольтные и низковольтные вводы, магнитопровод, бак трансформатора и т.д. С другой стороны, для трансформаторной подстанции трансформатор удобнее представить как элемент, у которого есть свои характеристики надежности, нормативно-техническая документация, требования к эксплуатации.
В соответствии с ГОСТ 27.002-89 для количественной оценки надежности применяются количественные показатели оценки отдельных ее свойств: безотказности, долговечности, ремонтопригодности и сохраняемости, а также комплексные показатели, характеризующие готовность и эффективность использования технических объектов (в частности, электроустановок).
Эти показатели позволяют проводить расчетно-аналитическую оценку количественных характеристик отдельных свойств при выборе различных схемных и конструктивных вариантов оборудования (объектов) при их разработке, испытаниях и в условиях эксплуатации. Комплексные показатели надежности используются главным образом на этапах испытаний и эксплуатации при оценке и анализе соответствия эксплуатационно-технических характеристик технических объектов (устройств) заданным требованиям.
На стадиях экспериментальной отработки, испытаний и эксплуатации, как правило, роль показателей надежности выполняют статистические оценки соответствующих вероятностных характеристик. В целях единообразия все показатели надежности, в соответствии с ГОСТ 27.002-89, определяются как вероятностные характеристики. В данном пособии отказ объекта рассматривается как случайное событие, то есть заданная структура объекта и условия его эксплуатации не определяют точно момент и место возникновения отказа. Принятие этой, более распространенной, концепции предопределяет широкое использование теории вероятностей [4, 7, 9, 11,13, 15].
2.1. Основные показатели безотказности объектов
2.1.1. Вероятность безотказной работы
Вероятность безотказной работы - это вероятность того, что в пределах заданий наработки отказ объекта не возникает. На практике этот показатель определяется статистической оценкой
 (2.1)
(2.1)
где No - число однотипных объектов (элементов), поставленных на испытания (находящихся под контролем); во время испытаний отказавший объект не восстанавливается и не заменяется исправным; n(t) - число отказавших объектов за время t.
Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени, причем она является убывающей функцией и может принимать значения от 1 до 0.
График вероятности безотказной работы объекта изображен на рис. 2.1.
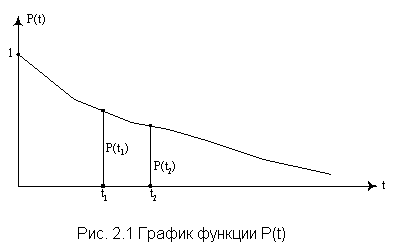
Как видно из графика, функция P(t) характеризует изменение надежности во времени и является достаточно наглядной оценкой. Например, на испытания поставлено 1000 образцов однотипных элементов, то есть No = 1000 изоляторов.
При испытании отказавшие элементы не заменялись исправными. За время t отказало 10 изоляторов. Следовательно P(t) = 0,99 и наша уверенность состоит в том, что любой изолятор из данной выборки не откажет за время t с вероятностью P(t) = 0,99.
Иногда практически целесообразно пользоваться не вероятностью безотказной работы, а вероятностью отказа Q(t). Поскольку работоспособность и отказ являются состояниями несовместимыми и противоположными, то их вероятности [4,13] связаны зависимостью:
Р(t) + Q(t) = 1, (2.2)
следовательно:
Q(t) = 1 - Р(t).
Если задать время Т, определяющее
наработку объекта до отказа, то Р(t) = P(T і t), то есть вероятность безотказной
работы - это вероятность того, что время Т от момента включения объекта до
его отказа будет больше или равно времени t, в течение которого
определяется вероятность безотказной работы. Из вышесказанного следует,
что ![]() . Вероятность отказа есть функция распределения времени работы Т
до отказа:
. Вероятность отказа есть функция распределения времени работы Т
до отказа: ![]() . Статистическая оценка вероятности отказа:
. Статистическая оценка вероятности отказа:
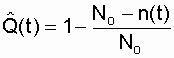 ; < (2.3)
; < (2.3)
Из [4, 13, 15] известно, что производная от вероятности отказа по времени есть плотность вероятности или дифференциальный закон распределения времени работы объекта до отказа
 . (2.4)
. (2.4)
Полученная математическая связь позволяет записать
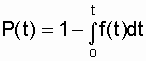 .
.
Таким образом, зная плотность вероятности ¦ (t), легко найти искомую величину P(t).
На практике достаточно часто приходится определять условную вероятность безотказной работы объекта в заданном интервале времени Р (t1, t2) при условии, что в момент времени t1 объект работоспособен и известны Р (t1) и Р (t2). На основании формулы вероятности совместного появления двух зависимых событий, определяемой произведением вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило [4, 13], запишем
![]() , откуда
, откуда
 . (2.5)
. (2.5)
По известным статистическим данным можно записать:
 ,
,
где N (t1), N (t2) - число объектов, работоспособных соответственно к моментам времени t1 и t2:
![]() .
.
Отметим, что не всегда в качестве наработки выступает время (в часах, годах). К примеру, для оценки вероятности безотказной работы коммутационных аппаратов с большим количеством переключений (вакуумный выключатель) в качестве переменной величины наработки целесообразно брать количество циклов "включить" - "выключить". При оценке надежности скользящих контактов удобнее в качестве наработки брать количество проходов токоприемника по этому контакту, а при оценке надежности движущихся объектов наработку целесообразно брать в километрах пробега. Суть математических выражений оценки P(t), Q(t), f(t) при этом остается неизменной.
2.1.2. Средняя наработка до отказа
Средней наработкой до отказа называется математическое ожидание наработки объекта до первого отказа T1.
Вероятностное определение средней
наработки до отказа [13] выражается так: 
Используя известную связь между f(t),
Q(t) и P(t), запишем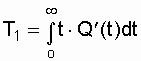 , а зная, что
, а зная, что![]() , получим:
, получим:
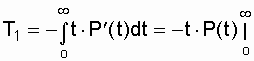 +
+ 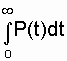 .
.
Полагая, что![]() и учитывая, что Р(о)
= 1, получаем:
и учитывая, что Р(о)
= 1, получаем:
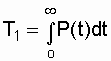 . (2.6)
. (2.6)
Таким образом, средняя наработка до отказа равна площади, образованной кривой вероятности безотказной работы P(t) и осями координат. Статистическая оценка для средней наработки до отказа определяется по формуле
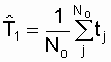 , ч. (2.7)
, ч. (2.7)
Интенсивность отказов - это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не наступил. Из вероятностного определения следует, что
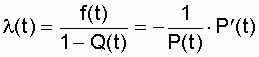 . (2.8)
. (2.8)
Статистическая оценка интенсивности отказов имеет вид :
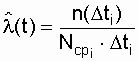 , (2.9)
, (2.9)
где ![]() - число отказов
однотипных объектов на интервале
- число отказов
однотипных объектов на интервале ![]() , для которого
определяется
, для которого
определяется ![]() ;
; ![]() - число работоспособных объектов в середине интервала
- число работоспособных объектов в середине интервала ![]() (см. рис.
2.2).
(см. рис.
2.2).
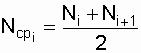 ,
,

 , (2.10)
, (2.10)где Nо - количество объектов,
поставленных на испытания; ![]() - интервал,
продолжающий время t;
- интервал,
продолжающий время t; ![]() - количество отказов
на интервале
- количество отказов
на интервале ![]() .
.
Умножив и поделив в формуле (2.10) правую часть на Nо и перейдя к предельно малому значению D t, вместо выражения (2.9), получим
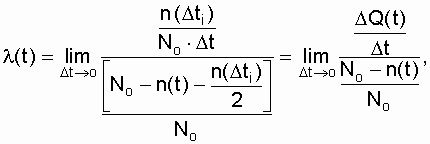
где 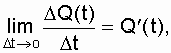 а
а 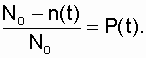
Следовательно,
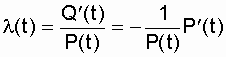 ,
,
что и записано в вероятностном определении l (t), см. выражение (2.8).
Решение [13] выражения (2.8) дает:
 или
или  .
(2.11)
.
(2.11)
Выражение (2.11) показывает связь l (t) и P(t). Из этой связи ясно видно, что по аналитически заданной функции l (t) легко определить P(t) и Т1:
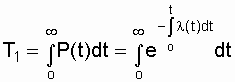 . (2.12)
. (2.12)
Если при статистической оценке ![]() время
эксперимента разбить на достаточно большое количество одинаковых
интервалов D t за
длительный срок, то результатом обработки опытных данных будет график,
изображенный на рис. 2.3.
время
эксперимента разбить на достаточно большое количество одинаковых
интервалов D t за
длительный срок, то результатом обработки опытных данных будет график,
изображенный на рис. 2.3.
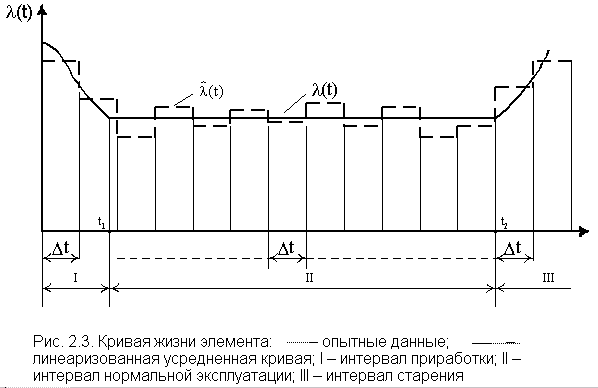
Как показывают многочисленные данные
анализа надежности большинства объектов техники, в том числе и
электроустановок, линеаризованная обобщенная зависимость l (t) представляет собой сложную
кривую с тремя характерными интервалами (I, II, III). На интервале II
(t2 - t1) l = const. Этот интервал может составлять более 10 лет [8], он
связан с нормальной эксплуатацией объектов. Интервал I (t1 - 0)
часто называют периодом приработки элементов. Он может увеличиваться или
уменьшаться в зависимости от уровня организации отбраковки элементов на
заводе-изготовителе, где элементы с внутренними дефектами своевременно
изымаются из партии выпускаемой продукции. Величина интенсивности отказов
на этом интервале во многом зависит от качества сборки схем сложных
устройств, соблюдения требований монтажа и т.п. Включение под нагрузку
собранных схем приводит к быстрому "выжиганию" дефектных элементов и по
истечении некоторого времени t1 в схеме остаются только
исправные элементы, и их эксплуатация связана с l = const. На интервале III (t >
t2) по причинам, обусловленным естественными процессами
старения, изнашивания, коррозии и т.д., интенсивность отказов резко
возрастает, увеличивается число деградационных отказов. Для того, чтобы
обеспечить l = const
необходимо заменить неремонтируемые элементы на исправные новые или
работоспособные, отработавшие время t << t2.
Интервал
l = const cоответствует экспоненциальной модели распределения
вероятности безотказной работы. Эта модель подробно проанализирована в
подразделе 3.2. Здесь же отметим, что при l = const значительно упрощается
расчет надежности и l
наиболее часто используется как исходный показатель надежности элемента
[14, 18, 19].
2.1.4. Средняя наработка на отказ
Этот показатель относится к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работу и продолжает работу до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений - поток восстановлений.
Средняя наработка на отказ объекта (наработка на отказ) определяется как отношение суммарной наработки восстанавливаемого объекта к числу отказов, происшедших за суммарную наработку:
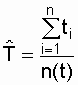 , (2.13)
, (2.13)
где ti - наработка между i-1 и i-м отказами, ч; n(t) - суммарное число отказов за время t.
2.1.5. Параметр потока отказов
Этот показатель также характеризует восстанавливаемый объект и по статистическим данным определяется с помощью формулы:
 , (2.14)
, (2.14)
где n(t1) и n(t2) - количество отказов объекта, зафиксированных соответственно, по истечении времени t1 и t2.
Если используются данные об отказах по определенному количеству восстанавливаемых объектов, то
 , (2.15)
, (2.15)
где ![]() - количество отказов по
всем объектам за интервал времени
- количество отказов по
всем объектам за интервал времени ![]() ; Nо -
количество однотипных объектов, участвующих в эксперименте (отказавший
объект восстанавливается, Nо = соnst). Нетрудно увидеть, что
выражение (2.14) похоже на выражение (2.8) с той лишь разницей, что при
определении
; Nо -
количество однотипных объектов, участвующих в эксперименте (отказавший
объект восстанавливается, Nо = соnst). Нетрудно увидеть, что
выражение (2.14) похоже на выражение (2.8) с той лишь разницей, что при
определении ![]() предполагается моментальное восстановление отказавшего объекта
или замена отказавшего однотипным работоспособным, то есть Nо =
соnst.
предполагается моментальное восстановление отказавшего объекта
или замена отказавшего однотипным работоспособным, то есть Nо =
соnst.
Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта. Отказы объектов возникают в случайные моменты времени и в течение заданного периода эксплуатации наблюдается поток отказов. Существует множество математических моделей потоков отказов. Наиболее часто при решении задач надежности электроустановок используют простейший поток отказов - пуассоновский поток [13, 15]. Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствия последствия.
Стационарность случайного
процесса (времени возникновения отказов) означает, что на любом промежутке
времени ![]() вероятность возникновения n отказов зависит только от n и
величины промежутка
вероятность возникновения n отказов зависит только от n и
величины промежутка ![]() , но не зависит от
сдвига
, но не зависит от
сдвига ![]() по оси времени. Следовательно, при
по оси времени. Следовательно, при ![]() вероятность появления
n отказов по всем интервалам составит
вероятность появления
n отказов по всем интервалам составит
![]() .
.
Ординарность случайного
процесса означает, что отказы являются событиями случайными и
независимыми. Ординарность потока означает невозможность появления в один
и тот же момент времени более одного отказа, то есть ![]() .
.
Отсутствие последствия
означает, что вероятность наступления n отказов в течение
промежутка ![]() не зависит от того, сколько было отказов и как они распределялись
до этого промежутка. Следовательно, факт отказа любого элемента в системе
не приведет к изменению характеристик (работоспособности) других элементов
системы, если даже система и отказала из-за какого-то
элемента.
не зависит от того, сколько было отказов и как они распределялись
до этого промежутка. Следовательно, факт отказа любого элемента в системе
не приведет к изменению характеристик (работоспособности) других элементов
системы, если даже система и отказала из-за какого-то
элемента.
Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно и если старение элементов отсутствует (l = const), то поток отказов в системе можно считать простейшим.
Случайные события, образующие простейший поток, распределены по закону Пуассона [4,13, 15]:
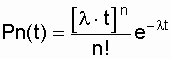 при n і 0 (2.16)
при n і 0 (2.16)
где Рn(t) - вероятность возникновения в течение времени t ровно n событий (отказов); l - параметр распределения, совпадающий с параметром потока событий.
Если в выражении (2.16) принять n = 0,
то получим ![]() - вероятность безотказной работы объекта за время t при
интенсивности отказов l =
const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии
восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, мы обязаны
записать w(t) = const;
l = w [13]. Это свойство широко
используется в расчетах надежности ремонтируемых устройств. В частности, в
[9, 10, 14, 18, 21] важнейшие показатели надежности оборудования
электроустановок даны в предположении простейших потоков отказов и
восстановлений, когда
- вероятность безотказной работы объекта за время t при
интенсивности отказов l =
const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии
восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, мы обязаны
записать w(t) = const;
l = w [13]. Это свойство широко
используется в расчетах надежности ремонтируемых устройств. В частности, в
[9, 10, 14, 18, 21] важнейшие показатели надежности оборудования
электроустановок даны в предположении простейших потоков отказов и
восстановлений, когда  и
соответственно
и
соответственно  .
.