УДК 621.313.33. СШ. 4.004.5

The control of air–gap uniformity  of the asynchronous machine over value of synchronous inductive resistance

Rogozin, cand.tech.sci., Lapshina. N.S, eng.

Донецкий государственный технический университет

e-mail автора rgg@elf.dgtu.donetsk.ua

Приведеная статья является переводом статьи «Косвенный контроль неравномерности воздушного зазора асинхронной машины по значению синхронного индуктивного сопротивления». Г. Г. Рогозин, канд. техн. наук, Н. С. Лапшина, инж. ДонНТУ.
Перевод осуществлён Лозицким Ю.В. yurilozitski@yandex.ru

Absence of effective ways of indirectly control of air–gap uniformity of asynchronous machines can be carried to one of unresolved problems of industrial power. A perspective direction of these decisions is the establishment and use with a view of technical diagnostics criteria estimations of parametrical effect – the phenomenon connected with air–gap non–uniformity and change of inductive resistance of the machine.

One of the important preconditions of such approach was development of techniques [Srs. 1–4], allowing with necessary, accuracy for the considered purposes to make measurement of equivalent parameters of the principal scheme of electric machines of an alternating current. It gives the certain advantages in comparison with settlement methods of definition of electromagnetic parameters in conditions of infringement of symmetry of an air–gap that, as is known, is connected with the decision of a challenge of a three–dimensional magnetic field.

Development and research of the mathematical model reflecting effect of change of synchronous inductive resistance – one of the most sensitive parameters of the machine – for the set air–gap non–uniformity, is the actual problem creating a basis for an establishment of criteria of working capacity, necessary for realization of the effective indirect control of uniformity of an air–gap.

Believing, that the deflection of a shaft and relative shift of the centers of stator and rotor magnetic systems are absent, position of a rotor and stator chisele of asynchronous machine can be unequivocally certain at use of three–dimensional system of coordinate axes. However in some cases use of two independent two–dimensional coordinate axes located in planes of face sections stator chisele of the machine (fig. I) is represented to more expedient. Components of vectors eccentricity on horizontal х and vertical y to axes in the specified sections are given in next expressions

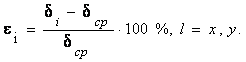                                         (1)

where δ_ср – average value of air-gap length in face section stator chisele; δ_i – air-gap length in a direction of chosen mutually perpendicular axes in face sections.

Using designations fig. 1 for the set intermediate section stator chisele l_j, applying a known rule of the vector analysis about division of a piece in the set parity, we have:

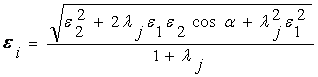,                              (2)

where ε1, ε2–modules of vectors eccentricity in first and the second face sections stator chisele, %;

;

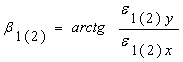α = β₁ – β₂ ;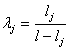   

l – length stator core, accepted to equal unit.

Synchronous inductive resistance of the asynchronous machine can be calculated on expression [Srs. 3]:

                                               (3)

where x_s=0,ε≠0 synchronous inductive resistance of the asynchronous engine at absence of air–gap non–uniformity, per.  unit; the k–factor considering relative is increased; ш synchronous inductive resistance at entry conditions ε1= ε2=100%; α=0.

For asynchronous and synchronous machines with the smooth rotor, pairs poles having number more than two, it is possible to accept approximately k =0.2∙10–2.

For approximation resulted above integrated dependence by the equation of regress it was used known of the theory of planning of factorial experiment [Srs. 5] the orthogonal central–composite plan (OCCP) the second order. Coding of values of components of vectors eccentricity ε1 and ε2 within the limits of from–1,414 (ε =  –100%) till 4–1.414 (ε = 100%) in a considered case leads to that for of some planned experiments of border of a modeled hyper surface of the response (synchronous inductive resistance) fall outside the limits physical realization of air–gap non–uniformity .

Fig. 1. Coordinate axes of model of air–gap non–uniformity of the asynchronous machine.

The equation of regress of required mathematical model has a following appearance:

The equation (4) and expression (3) can used for calculation of synchronous inductive resistance at zero entry conditions (x_s=0,ε=0) for this purpose it is necessary to have data of calculation on (4) and skilled measurement according to a technique [Srs. 4] synchronous inductive resistance at the any entry conditions, two vectors characterized by four components eccentricity in face sections stator chisele. Practical interest represents also use (4) for definition of coordinates of an axis of a rotor concerning an axis stator chisele by results of skilled measurement of synchronous inductive resistance at four (or more) consecutive test moving of a rotor to a direction of the accepted coordinate axes (fig. I).

For analytical research of functional dependence between synchronous inductive resistance and changes of an air–gap it is expedient to reduce quantity of independent factors. Using the concept of a vector entered above eccentricity in face sections stator chisele , we shall present approximated system dependent on factors ε1, ε2 and (fig. 1) – By means of OCCP the second order for three independent variables we shall receive the equation of regress of a kind:

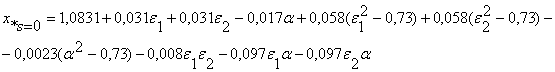         (5)

Errors of approximation of a surface of the response in three–dimensional space of coordinates for each of fifteen experiments of the plan do not exceed 1,1 %.

For definition of the minimal values of synchronous inductive resistance at all possible changes eccentricity within the limits of its set maximal values in face sections stator chisele sections of a surface of the response paid off at the values ε1 equal 100; 87,5; 75; 62,5; 50 %. Thus value eccentricity ε2, varied in the second face section stator chisele (at all possible values of a corner), did not exceed specified above values.

As an example we shall consider results of the analysis of section of a surface of the response at ε1=100 the %, representing the greatest interest. Obviously equation of regress necessary for research can be received from (5) after substitution ε1 = + 1,215. However for reception of more exact results we shall take advantage of the equation of regress received on the basis of OCCP of the second order, approximating synchronous inductive resistance з planes only two variables ε2 and:

x_s=0,ε=0 = 1,1244+0,027ε2 – 0,0277α+0,0078(ε2² – 2/3) – 0,0066(α² – 2/3) – 0 ,025ε2α                    (6)

After reduction (6) to an initial kind by carry of the beginning of axes of coordinates to a special point (ε2 =–1,267, а=0,291) and their turn on a corner 0 = –29°57 we shall receive:

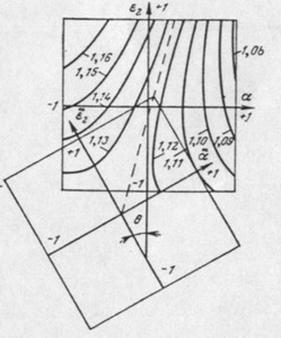
Fig. 2. Planimetric curves of factorial space of synchronous inductive resistance at value eccentricity in first of face section stator chisele, equal 100 %.

x_s=0,ε=0 = 0,015 –0,0139 +1,124                                 (7)

The equation (7) describes a hyperbolic paraboloid. As signs on factors at unknown persons different to the rights the part of the equation represents a surface of type "minimax" with the equation asymptots:

                                                   (8)

As follows from fig. 2, minimally possible for a considered condition (ε1=100 %) value of synchronous inductive resistance is equal approximately 1,082 x_s=0,ε=0. As the planimetric curve of this value of resistance (at α≈±1) is extended lengthways, axes ε2 exact definition is direct under the schedule of the second coordinate of an extreme point inconveniently.

Calculations on (3) and vicinities α=±1 variations ε2 have allowed to receive following specifications of a required minimum and its coordinates:

x_*s=0 = 1,082;  ε2 = 37,5%;      α = 180˚

Similarly under condition of ε2 ε1 were analyzed sections of investigated function for other values ε1. A number of minima of function x_*s=0 depending on the maximum permissible values set in planned area eccentricity has been as a result received. The specified minima of function are certain in the table as much as possible admissible values of synchronous inductive resistance of the asynchronous machine. In the same place values of corresponding coordinates of investigated function are resulted.

As much as possible admissible values of synchronous inductive resistance take place at opposite directed displacement of the ends has fallen a rotor of the asynchronous machine, thus of a parity, ε2/ε1 in face sections stator chisele at ε1> 50 % are within the limits of 0,375–0,5. At displacement only one end of a shaft (ε2=0) as much as possible admissible values of resistance x_*s=0 will be at values eccentricity ε1, approximately on 17 % less limiting. At radial displacement of a rotor and both face stator sections in one party (α = 0) and ε1 = ε2 same values x_*s=0  are reached at twice smaller values eccentricity, than in case of unilateral displacement.

Data cited in the table allow to prove also a choice of factor of a stock on change of synchronous inductive resistance at the control of working capacity of the asynchronous machine over this parameter. With this purpose it was considered dependences. Factor

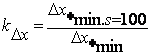
in function of factor of a stock on value set maximum permissible eccentricity machines

The factor  k_Δх reflects of adjust degree an admissible increment of synchronous inductive resistance of the asynchronous machine in operation from it « emergency values »

In the analytical form of the record using approximating Lagrange polynom, the specified dependence (with a margin error no more than 2 %) look like:

k_Δх = –0,255+1,407 k_s –0,1515 k²_s

Thus, the generalized criterion of working capacity of the machine, based on parametrical effect of air–gap non–uniformity, can be expressed by parity:

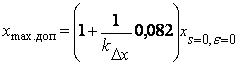
The given tables and dependences (0) show, that отстройка from as much as possible admissible increase synchronous inductive the resistance, corresponding eccentricityу in one of face sections of the rotor, equal 100 %, with factor of a stock k_Δх =2 theoretically provides revealing growth eccentricity at achievement by the last in one of face sections 50 of %. However at measurement of synchronous inductive resistance by means of integrating devices with accuracy of 1 % [Srs. 4] value eccentricity can appear 63 % equal approximately (see the table). In a kind of that character of the schedule corresponding (9), is close to linear dependence, a zone of a possible error of measurements correspond to a zone controllable eccentricity (for any preset value) within the limits of ±13 % of border of a field of the admission.

List of sources

1.     Казовский Е. Я – Переходные процессы в электрических   машинах   переменного   тока. — М.:   АН   СССР,   1962.

2.     Гашимов М. А. Вопросы исследования нес им метрик воздушного зазора электрических машин: Автореф. дис. на соиск. учен. степени к–та техн. наук. Баку, 1972.

3.     Рогозин Г. Г., Лапшина Н. С. Косвенный контроль неравномерности  воздушного зазора  асинхронных  машин.— Электротехника. 1980, № 3.

4.     Рогозин Г. Г., Лапшина Н. С. Определение индуктивных сопротивлений схемы замещения синхронной машины при неподвижном роторе. — Электротехника, 1976, № 6.

5.     Ивоботенко Б. А.,  Ильинский И. Ф–, Копылов И. П. Планирование эксперимента в электромеханике. — М.: Энергия, 1975.