IMPACT OF THE AIR GAP ECCENTRICITY ON THE LEAKAGE FLUX
CHANGE OUTSIDE THE IM FRAME DURING RUN-OUT OF THE MOTOR
AFTER DISCONNECTION FROM THE SUPPLY
G.G. Rogozin
National Technical University of Donetsk
Department of Electrical Engineering
58, Artem Sir., 83000 Donetsk, Ukraine
phone: +38(0622)910307-fax: +38(0622) 278-e-mail: rgg@elf.dgtu.donelsk.ua
Abstract
The paper is devoted to analyzing the influence of the air gap eccentricity on the electromagnetic quantities and transient processes in the phase-wound rotor of the 40 kW induction motor after switching off from the electrical network. The conclusion is drawn that the changes in the magnetic induction outside the IM frame can be used for determining the air gap eccentricity.
1-INTRODUCTION
There are the problems of saving the electrical energy and reliability of induction motors (IMs) that are of primary concern. Both of these problems manifest themselves at the air gap eccentricity. The mentioned phenomenon is a consequence of the gradual cutting wear of bearings, deformation of the end shields, etc. The indicated causes are responsible for the increase of the motor vibration and accelerate the wear of bearings. In some cases it is quite possible that the rotor will touch the inside surface of the stator. Such damages demand of carrying out the prolonged restoration repairs of IMs. As a result of eccentricity changes, it is known, the efficiency of an IM can decrease by 2.8 %, the - breakdown and locked rotor torques are reduced within the limits of 20 and 8 % correspondingly, the slip can increase by 10 %. The noticeable effect on the above mentioned operating variables becomes apparent as the eccentricity increases more than 30-35 percent. Sufficiently accurate but labour consuming method for monitoring the air gap eccentricity in IMs was based on using the direct current [1]. The modem on-line IM diagnostics, as a rule, is based on measuring and processing the phase armature currents and terminal voltages. The above mentioned data are the secondary operational variables of the corresponding metering transformers. Meanwhile the most part of IMs, from the standpoint of the total consumed active power, belong to the low voltage range and is not equipped with transformers. Under these conditions the new approach of using, as a test parameter, the leakage flux appearing outside the IM frame during decaying the aperiodic current rush in a rotor winding (or a rotor squirrel cage) after switching off an IM from the electrical network for a short time (not more 3 s) is of prime interest. The application of the mentioned approach that uses as an input impulse signal the switched armature current of an IM under its normal transient process offers a number advantages over the conventional methods, in particular, it offers the prospects of designing the specialized portable devices for testing the air gap eccentricity.
2. - ANALYSIS OF AIR GAP ECCENTRICITY INFLUENCE ON EQUIVALENT-CIRCUIT PARAMETERS OF IMs
Magnetic flux of an IM disconnected from the power supply system includes the space zones associated with the air gap as well as with rotor slots, rotor end rings, differential and tooth leakage permeances being denoted by X,2, X,2, Xd2 and Ä,2 respectively. Making use of the geometrical dimensions and the mathematical model of the Ằ based on the set of design equations the permeance components for leakage flux linkage at the given air gap eccentricity were calculated (in dimensionless quantities).
With the stator winding disconnected from the power supply the alterations in tooth and differential leakage permeances is found to be of prime interest for the problem set up. The changes in the mentioned permeances as a function of the eccentricity are analyzed below in some detail. Consideration is given with (and wimout) taking into account the saliency of the stator and rotor cores.
The results of engineering design of the IM total electromagnetic quantities have been obtained on making certain universally adopted assumptions as follows:
• ferromagnetic cores have an infinitly large permeability in comparison with that of free space;
• possibility of applying the principle of superposition to treat the magnetic field of the machine as the sum of the fields set up by each of its windings and separate components;
• diminishing all the stator phase currents to zero, when disconnecting off an Ằ from the external circuit, rapidly, i.e. during the time span when an arc exists between the contacts interrupting the stator circuit.
The above mentioned findings for the IM ̀À36-41/8Ô (40 kW, 380/660 V, 730 r.p.m.) are given in the Table 1.
Table 1. Electromagnetic quantities of the ̀À36-41/8Ô induction motor
Permeances |
Equivalent-circuit parameters, p.u. |
|||||
|
|
|
|
|
|
|
3.479 |
0.380 |
0.0163 |
0.082 |
1.963 |
0.0236 |
0.1461 |
The tooth leakage permeance depends on the air gap changes within the limits of a tooth pitch. The mentioned relationship is dependent upon ratio between the width of opening the slot towards the air gap (b) and the radial length of the air gap (5). The latter one along the radial tooth axis was determined from the formula
(1)
were ε - rotor eccentricity; φ - space angular coordinate counted out from the minimum air gap length (δmin). The influence of the air gap eccentricity on the tooth leakage permeances was calculated by the expression [2]
(2)
The leakage permeance Xa under consideration for the ̀À36-41/8Ô IM at the uniform air gap is equals 0.1227. The graphical representation of X,2 versus b/S in the range 2(50 ă S 2 0 is shown in the Figure 1 for two coordinate axes along the absciss.
Figure 1. - Changes in the rotor tooth leakage permeance of the ̀À36-41/8Ô Ằ with the ratio b/δ
The design dependence 
calculated with the use of the curve 
is presented in the Figure 2. In the construction of this Figure was assumed that
The relationship shown in the Figure 2 was calculated by the equation
(3)
where the numerator presents the sum of the rotor tooth leakage permeances above the each slot.
The design expression for calculating die differential leakage permeance of the rotor [2] takes the form
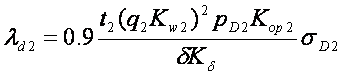(4)
where 
_ coefficient dependent on the ratio between the slot
opening and the slot pitch (t2), 
- rotor
damping coefficient; q2- number of slots per pole per phase; 
- winding factor; 
-
air gap factor
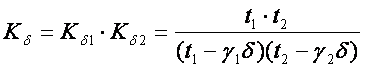(5)
- factor of the differential leakage; γ1, γ2-coefficients dependent on 
;
- slot width at the air gap; t1, t2- stator and rotor slot pitches.
Figure 2. - Dependence of the rotor tooth relative leakage permeance with the ̀À36-41/8Ô IM rotor eccentricity
The results of calculating the differential leakage permeance versus the eccentricity from the equation (4) are given in the Figure 3.
The dependences 
and 
were obtained by die use of equations
and 
where
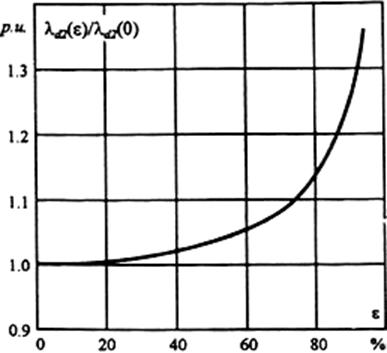
Figure 3. - Dependence of the rotor differential relative leakage permeance with the ̀À36-41/8Ô IM rotor eccentricity
3. - SIMULATION OF THE AIR GAP ECCENTRICITY IMPACT ON DECAYING THE ROTOR CURRENT AFTER DISCONNECTING THE Ằ FROM THE SUPPLY
3.1 - Analysis of the eccentricity impact on the IM and gap permeance
The design main mutual and leakage reactances of the IMs being considered were used for calculating the electromagnetic transient processes, namely, the decay of the rotor current from its initial value and, consequently, the change of the magnetic induction with time.
In line with me well-known expression for determining the air gap specific magnetic permeance without considering the toothed core and saturation phenomenon
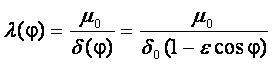(6)
where in accordance with me Fourier's
harmonic expansion 
; φ- electrical angle defining the position of the rotor relative to me
reference axis (origin); λ0,
λ1 - permeance components
when using the simplest expansion row [2],
,
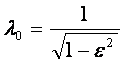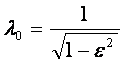
Taking into account the influence of the double-sided toothed core (q1(2)) on the fundamental harmonic of air gap magnetic flux [2]
(7)
The results obtained by use of expression (7) for the ̀À36-41/8Ô induction motor are illustrated in the Figure 4.
Figure 4. - Changes is air gap permeance of the IM versus eccentricity:
1 - q1(2)= 0
; 2 - q1(2) 
0
As indicated in the Figure 4 the air gap permeance essentially depends on the eccentricity at its values above 50 %.
3.2 -Transients after disconnecting the IM from external circuit
The rotor current phasor (I2 ) can be determined from the equation for the short-circuited rotor winding
with the stator winding open-circuited. The rotor equation, using a set of axes
rotating at an arbitrary velocity 
,
can be written in the form
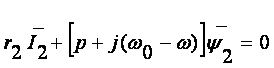(8)
where 
- rotor flux linkage equal to its intrinsic component, 
Using the d- and q- axes rotating at the rotor velocity ω0=ω, we can obtain the following solution of the above initial equation
(9)
where τ2–time constant of the rotor winding, τ2 = x2 / r2.
The resultant rotor current phasor I2 corresponds to a set of aperiodic currents in the rotor phases
where a = åơđ(j2π/3), a = exp(-j2π/3). The change in the rotor magnetic flux induction after disconnection of the IM from the power supply follows the pattern seen in the rotor current, that is
(10)
As can well be imagined the change in the voltage across the terminals of the IM depends on the rotor speed and magnetic saturation along the path of the mutual field. The change in the magnetic induction with account of the eccentricity impact was calculated by the use of the following expressions
, 
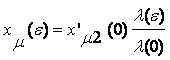
given in Figures 5, 6.
The change in the rotor time constant at the open-circuited stator winding calculated by the expression
is shown in the Figure 7.
As may be inferred from the graph the change in the magnetic induction flux leakage, in concept, can be used in the warning diagnostics of the Ằ eccentricity by the approach considered.
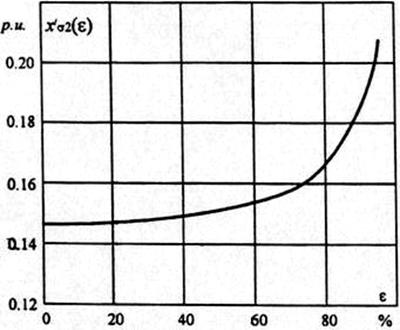
Figure 5. - Change in the rotor winding reactance of the ̀À36-41/8Ô IM
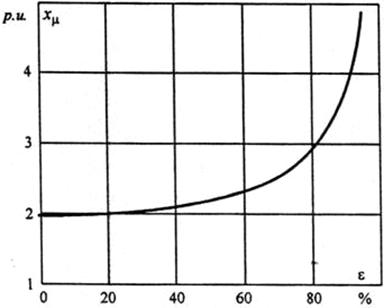
Figure 6. - Change in the mutual reactance oftheMA36-41/8Ô IM
Figure 7. - Relationship of the rotor time constant versus eccentricity of the
̀À36-41/8Ô IM after disconnection from the supply
4. - EXPERIMENTAL DATA
The experimental arrangement included the above mentioned unique slip-ring motor of the ̀À36-41/8Ô type and the device for the digital signal registration. The IM was equipped with the plug-in type bearings located in the eccentric disk.
The instantaneous phase currents 
of the rotor measured
at zero and 50 per cent eccentricity level were used for calculating the rotor
current phasors by the formula
(12)
The time-dependences of the above mentioned rotor current phasors and their difference are shown in the Figure 8.
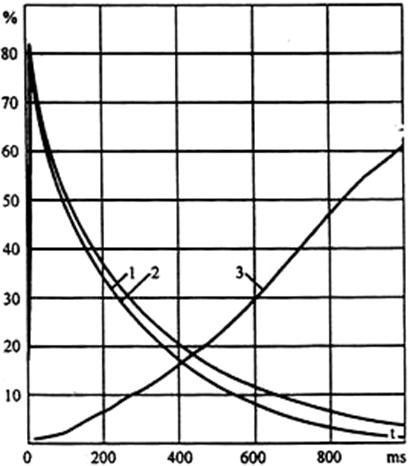
Figure 8. - Time-dependences of the ̀À36-41/8Ô IM rotor current phasors:
1 - IM without eccentricity (ε = 0); 2 - IM ε = 50 %; 3 - deviation of the 2nd curve from the 1st (standard) one
Maintenance diagnostics of the eccentricity in IMs can be based on using the methods of the pattern recognition theory or those based on the absolute deviation between the measurements at the given time multiple of the time constant at the zero eccentricity and the definite temperature. The standard time constant (τst) should be previously reduced to the current diagnostic check temperature (τd.ch) by the formula
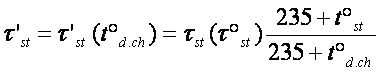(13)
It is obvious that in this instance the standard magnetic induction at the definite temperature tdch can be obtained by the expression
where 
As is clear from a more sophisticated analysis of the curves 1, 2 shown in the Figure 8 the latter ones can be presented by several exponential components. This phenomenon adequately agrees with the influence of saturation effect on the path of the main magnetic flux and manifests itself in the initial stage of the transient process in a short time interval (approximately 100 ms at s = 0and 150 ms at ε = 50%).
In the case being considered the IM was switched off the electrical network at the no-load condition. At the first instant of disconnecting the same IM at rated load the rotor current will be less than in the former case. So, the fast decaing components in the rotor current and the leakage flux outside the IM frame can be absent in the diagnostical signal.
5.-CONCLUSION
The leakage flux change outside the induction motor frame, independent of the rotor slip, can be used for detecting the air gap eccentricity at the IM run-out after disconnection from the electrical network. The Hall sensor data display obtained through the use of the digital signal registration of the leakage flux induction, at the point positioned nearby the outside end shield surface of the induction motor, reflects the rotor current rush appearing at the first instant of the stator disconnection. At the succeeding time periods, due to the rotor revolution, the generalized vector of the induced rotor currents (in accordance with the law ef electromagnetic inertia of the rotor resulting flux linkage) and its leakage magnetic flux rotate with the rotor angular velocity relative to the Hall sensor. The oscillogram recorded under the diagnostic check represents, at a certain scale, the force-free rotor currents decaying with time. It is evident, from the above mentioned simulation, that the time constant of the leakage flux induction exponential decay is air gap eccentricity dependent.
REFERENCES
[1] Rogozin, G.G.; Lapshina, N.S.: Monitoring the
uniformity of the air gap in induction motors from the
value of the synchronous reactance. Electrichestvo,
no. U.pp.44-46, 1981 (in Russian).
[2] Sergeev, P.S.; Vinogradov, N.N.: Design of electrical
mashines. Moscow: Energia Publishers, 1970 (in
Russian).
[3] Geller, Â.; Gamata, V.: Higher harmonics in
asynchronous machines. Moscow: Energia Publishers,
1981 (in Russian).