|
Расчет нагрева обмоток глубокопазного асинхронного двигателя в пусковом режимеТехническая электродинамика. - 1984. -
№2. - С. 80 - 86 Бурковский А. Н., Голянд Б. С.,
Кублицкая Т. В., Родионенко Г. Я. Задача определения допустимого числа
включений подряд глубокопазнных асинхронных двигателей является весьма
актуальной и наиболее точно может быть решена на основе расчета полей
температур в обмотках при пусках. Способ расчета, изложенный в работе [б],
пригоден лишь для определения средних превышений температур по высоте
стержня ротора, что приемлемо лишь для двигателей с простой геометрией
паза ротора (с малым влиянием вытеснения тока). В глубокопазных роторах во
время переходного процесса превышения температур по высоте стержня резко
изменяются из-за неравномерной плотности потерь (например, при коротком
замыкании разница превышений температур верхней и нижней части стержня
достигает 80—100 °С [4]). Поэтому для достижения достаточной точности
расчета в математической модели необходимо учесть реальные зависимости
изменения пусковых потерь в обмотках статора и ротора от времени пуска и
изменения плотности потерь по высоте стержня ротора. При пуске электромагнитные параметры
двигателя, плотность потерь в обмотках и теплоотдача с их
поверхностей изменяются во времени по нелинейным зависимостям. Поэтому
целесообразно разделить время пуска на ряд интервалов, в пределах каждого
из которых указанные величины могут быть представлены их средними
значениями. Это позволит рассчитывать нагревы обмоток статора и ротора на
каждом интервале скольжения с усредненными значениями параметров схем
замещения. Тепловые схемы замещения статора и ротора составляют таким
образом, чтобы можно было непосредственно определить нагревы наиболее
теплонапряженных участков обмоток и железа сердечников. На рис. 1 [1]
показаны тепловые схемы замещения статора (а) и ротора (б).
Особенностью первой схемы является наличие четырех узлов, моделирующих
изоляцию вдоль секции (расчетная точка на середине
толщины изоляции), а во второй схеме — стержень обмотки по высоте
моделируется четырьмя участками с постоянной (условно) на каждом участке
плотностью потерь в пределах интервала времени изменения скольжения на
Токовую характеристику рассчитывают по
следующей формуле [2]:
Время пуска:
где
Принимая на каждом интервале
скольжения
где n—число интервалов
скольжения;Kп—коэффициент пропорциональности. Общее количество
тепла в обмотке статора за время пуска:
где Dk—диаметр круговой диаграммы;
Средний квадрат тока на i-м интервале
скольжения:
Коэффициент пропорциональности
потерь:
Далее производят расчет распределения
потерь по высоте стержня ротора и по узлам схемы замещения. Для расчета
распределения плотности тока стержень ротора по высоте разделен на ряд
(N) слоев с условно постоянной плотностью тока внутри каждого слоя
(например, бутылочнообразный паз—на 10 слоев, пусковая часть обмотки—на 6
слоев, а рабочая—на 4). Коэффициенты магнитной проводимости
а активные сопротивления слоев:
где
В схеме замещения стержня
………………………………………………………….. ………………………………………………………….. …………………………………………………………..
где
а) с учетом вытеснения тока
б) без учета вытеснения тока
где
а) сопротивление стержня
б) сопротивление кольца
где
Потери энергии в обмотке статора:
Потери энергии в обмотке ротора:
Потери энергии в стержнях:
Потери энергии в кольцах:
Тепловые схемы замещения описываются
системами обыкновенных дифференциальных уравнений, при этом в главных
коэффициентах матрицы проводимостей учитывается изменение греющих потерь
при изменении температуры [I]. Тепловые проводимости конвективно-го
теплообмена рассчитываются по средним значениям частоты вращения на каждом
интервале скольжения. За время выбега после отключения указанные
проводимости рассчитываются по средней частоте вращения, а во время паузы
учитывается естественная конвекция и лучеиспускание. Затем проводится
расчет нагрева обмоток статора и ротора. Результаты расчета нагрева
обмотки статора за время пуска фиксируются и сравниваются с допустимым
превышением температуры. Если превышения температуры всех узлов меньше
допустимых, то производится расчет кривой остывания (во время паузы),
расчет следующего пуска и т. д. При достижении допустимого превышения
температуры во время очередного пуска расчет заканчивается, при этом
фиксируется число пусков и кривая нагрева. После расчета нагрева ротора на
первом интервале времени пуска фиксируются превышения температур, далее
производится расчет распределения потерь по высоте при новом распределении
превышений температур, выполняется расчет нагрева на следующем интервале
времени и т. д. до завершения пуска; максимальное превышение температуры
сравнивается с 'допустимым и т. д. (как для обмотки
статора). Программа расчета допустимого числа
включений двигателей подряд оформлена в виде цикла, изменяемым параметром
которого является номер интервала скольжения и, соответственно, значение
скольжения на данном интервале. По окончании расчета очередного пуска
производится сравнение температур точек схем замещения статора и ротора
допустимыми температурами. Если значения расчетных температур меньше
допустимых, то рассчитывается остывание двигателя во время паузы и
очередной пуск, в противном случае счет прекращается. Для решения систем обыкновенных
дифференциальных уравнений использован метод Рунге—Кутта, который
позволяет интегрировать с переменным шагом, что сокращает время решения
систем уравнений. Так как программа достаточно объемная, то для удобства
трансляции отдельные ее блоки оформлены в виде автономных процедур.
Применяя этот режим, можно устранить большинство количественных
ограничений, присущих транслятору, так как в автономно запрограммированной
процедуре все локализованные в ней величины и константы располагаются в
самой процедуре. Машинное время экономится за счет того, что процедуры
повторно не транслируются. В режиме автономной трансляции процедур
оформлены следующие блоки программы: расчет распределения потерь в функции
времени пуска, расчет параметров тепловой схемы замещения статора, расчет
нагрева обмотки статора во время пуска и ее охлаждения во время паузы,
расчет параметров тепловой схемы замещения ротора. По окончании расчета печатаются
значения температур во всех точках схем замещения статора и ротора по всем
пускам, а также количество пусков. Печать результатов сопровождается
текстовыми пояснениями. Для пояснения логической структуры программы
введены комментарии. Программа расчета нагрева обмоток двигателя при
пусках подряд составлена на языке АЛГОЛ-60 для транслятора TA-IM на ЭВМ
М-222. Для проверки точности методики
выполнен расчет нагрева при пусках двигателя ВА02 450LB-4 мощностью 400
кВт с бутылочнооб-разным пазом ротора: пуски под нагрузкой с моментом
сопротивления В заключение можно отметить, что
описанный способ расчета нагрева обмоток асинхронного двигателя в пусковых
режимах применим для двигателей различных конструкций, отличающихся между
собой формами пазов, уровнями напряжения на зажимах и формами
характеристик момента сопротивления. 1.
Бурковский А. Н., Ковалев Е. Б., Коробов В. К. Нагрев и охлаждение
электродвигателей взрывонепроницаемого исполнения.—М.: Энергия, 1970.—185
с. 2.
Немченко Н. М. Отношение тока асинхронного двигателя к его току
холостого хода, как функция скольжения.—Изв. вузов. Электромеханика, 1981,
№3, с. 281— 284. 3.
Проектирование электрических машин/Под ред. И. П. Копылова, М.:
Энергия, 1980.—495 с. 4. Сарач
А. А. Исследование нагрева короткозамкнутых роторов асинхронных
двигателей в режиме короткого замыкания с учетом вытеснения тока. Автореф.
дис. ... канд. техн. наук, Новочеркасск, НПИ, 1976.—15
с. 5.
Филиппов М. Н. О расчете коэффициентов проводимости пазового
рассеяния электрических машин.—В кн.: Разработка и исследование
взрывозащищенного электрооборудования. Донецк, 1981, с.
40—48. 6.
Чертков М. А. Расчет нагрева обмоток асинхронного двигателя при
пуске.—Электричество, 1979, №6. с. 48—51. |
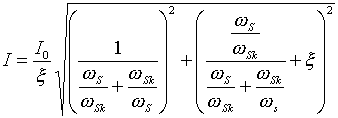
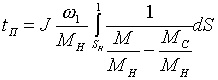 , (2)
, (2)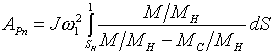 , (3)
, (3)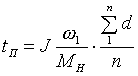 , (4)
, (4)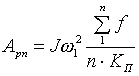 , (5)
, (5)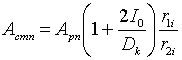 , (6)
, (6)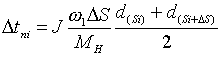 , (7)>
, (7)>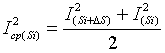 . (9)
. (9)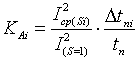 . (10)
. (10)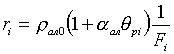 , (12)
, (12)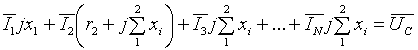 ;
;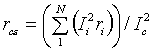 ; (13)
; (13)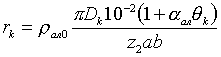 , (15)
, (15)