Сборник статей кафедры "Общая электротехника"
УДК 621. 313
ВЛИЯНИЕ НЕРАВНОМЕРНОСТИ ВОЗДУШНОГО ЗАЗОРА НА ЭЛЕКТРОМАГНИТНЫЕ ПАРАМЕТРЫ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ РОТОРА ПРИ ОТКЛЮЧЕНИИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
Рогозин Г.Л, Мироненко И.А.
Донецкий государственный технический
университет
mailto:rgg@elf.donntu.ru
The article is devoted to analysis of the influence of the air gap eccentricity on the electromagnetic quantities and transient processes in the rotor current after switching off two induction motors from an electrical network– The first part of the article deals with the eccentricity–dependences of the reactances being caused by the changes in the mutual field and the spatial pattern components of the magnetic field set up by the slot and differential leakage fields, leakage fields in the tooth and coil–end of a motor. The second part is about the results of the mathematical simulation of the changes in the rotor current analyzed for the MA 36–41/8Ф and BAOK 450 U–6 types induction motors.
Введение. Наиболее важные проблемы электроэнергетики связаны с сокращением потерь энергии и повышением надежности эксплуатации оборудования. Обе проблемы проявляются при возникновении неравномерности воздушного зазора, возникающего в асинхронных двигателях (АД). Указанное явление обуславливается абразивным износом подшипников, деформацией торцевых щитов машины, смешением фундаментов выносных подшипников и т.п. Поскольку воздушный зазор в АД весьма мал, то указанные причины вызывают высокую степень эксцентриситета ротора, что приводит к вибрации и ускоряет износ подшипников.
Известно, что в результате появления значительного эксцентриситета коэффициент полезного действия АД снижается на 2,8 %, максимальный и пусковой моменты уменьшаются в пределах 20 % и 8 % соответственно, скольжение увеличивается на 10 %. В наиболее тяжелых случаях возможно касание ротора за внутреннюю поверхность статора. Возникающие при этом повреждения требуют проведения продолжительного восстановительного ремонта АД. Затраты в этом случае соизмеримы со стоимостью новой машины.
К числу наиболее известных методов косвенного контроля неравномерности воздушного зазора (НВЗ) в настоящее время можно отнести метод контроля по величине синхронного индуктивного сопротивления [1], а также метод контроля по величинам индуктивного сопротивления короткого замыкания и нулевой последовательности, исследованных в ДПИ. К недостаткам указанных методов следует отнести:
- требование отключения АД от сети с подготовкой рабочего места по наряду;
- необходимость использования внешних источников постоянного или переменного тока для подачи диагностического воздействия на АД;
- значительное время проведения диагностического испытания (до 3–4 часов).
Указанные методы не нашли широкого применения в промышленности. Таким образом, задача создания более эффективного метода контроля НВЗ является актуальной. Целью настоящей работы является разработка метода диагностирования, исключающего приведенные недостатки.
Использование нормального переходного процесса кратковременного отключения АД в качестве тестового воздействия может иметь существенное преимущество перед известными методами. Опенка эффективности исследуемого экспресс–метода требует установления диагностического параметра машины, выбора возможного диагностического сигнала и оценки его чувствительности к нарушению равномерности воздушного забора.
1 Анализ влияния неравномерности воздушного зазора на электромагнитные параметры схемы замещения асинхронных двигателей
Основные допущения. При анализе влияния НВЗ асинхронной машины на электромагнитные параметры ротора при отключенной обмотке статора принимаются следующие допущения:
- магнитная проницаемость стали для ненасыщенного состояния магнитопровода статора и ротора, а также элементов их конструкции равна бесконечности, то есть μ = ∞ ;
- линии магнитной индукции в воздушном зазоре перпендикулярны поверхности ротора, а линии индукции поля пазового рассеяния пересекает паз прямолинейно, перпендикулярно его боковым стенкам;
- возможно рассматривать изменение магнитных полей рассеяния ротора АД без учета влияния поля основного магнитного потока (воздушного зазора), то есть пользоваться принципом наложения.
Исходные данные исследуемых асинхронных двигателей: МА36–41/8Ф (40 кВт, 380/660 В, 730 об/мин, 50,5/87 A, cos φ = 0,78), ВАОК 450 М–6 У2–5 (315 кВт, 500 В, 989 об/мин, 428 A, cos φ = 0,894).
Определение магнитных проводнмостей и индуктивных сопротивлений по коронкам зубцов и дифференциального рассеяния. Магнитное поле ротора, отключенного от обмотки статора АД, содержит пространственные зоны полей воздушного зазора, пазов ротора, лобовых частей, по коронкам зубцов, а также полей, относимых к дифференциальному рассеянию.
Результаты конструкторских расчетов электромагнитных параметров, проводимостей пазового (λП) и лобового (λЛ ) рассеяния роторов, полученные с использованием методики ВНИИВЭ, для исследуемых машин, приведены в табл.1.
Таблица 1 – К анализу проводимостей потоков рассеяния ротора
|
Тип двигателя |
Проводимости |
Электромагнитные параметры, о.е. | |||||
|
λП |
λЛ |
r1 |
xσ1 |
xμ |
r'2 |
x'2 | |
|
МА36–41/8Ф |
3,479 |
0,380 |
0,0163 |
0,082 |
1,963 |
0,0236 |
0,1461 |
|
ВАОК450 М–6 |
3,776 |
0,517 |
0,0127 |
0,0825 |
3,441 |
0,0130 |
0,1224 |
При возникновении НВЗ происходит изменение значения δ в пределах каждого зубцового деления ротора t2 .что, как следует из рис.1 [2], приводит к изменению проводимости λК, зависящей от отношения b/δ.
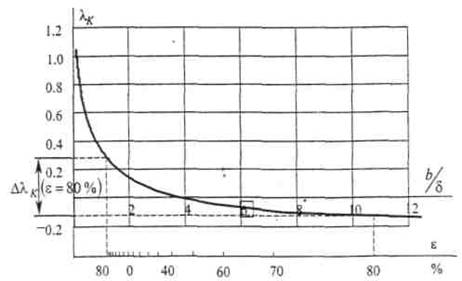
Рисунок 1 – Изменение проводимости по коронкам зубцов ротора двигателя
МА36–41/8Ф при НВЗ
Определение воздушного зазора по оси каждого паза ротора производилось
по выражению:
δ = δ0(l –ε cos φ),
( 1 )
где ε – эксцентриситет ротора; φ – пространственная (угловая)
координата, отсчитываемая от точки минимального зазора
δmin (см. рис. 2).
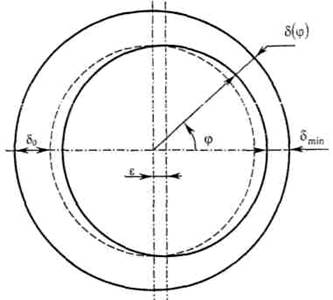
Рисунок 2 –
Пространственные координаты неравномерного воздушного зазора АД
Рассмотрим влияния НВЗ на изменение магнитной проводимости потоков рассеяния по коронкам зубцов АД МА36–41/8Ф и ВАОК450 М–6 У2–5.
В соответствии с выражением ( 2 ):
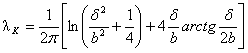 ,
( 2 )
,
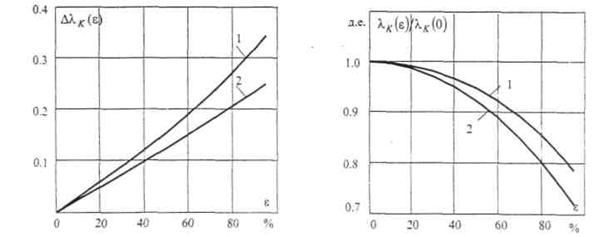
( 2 )График зависимости λК (b/δ), отражающий изменение величины воздушного зазора двигателя в пределах значений 2δ0 > δ > 0, показан на рис. 1 для двух координатных осей по оси абсцисс. Полученная с использованием рис. 1 зависимость ΔλК (ε) показана на рис. 3. При построении последнего принималось, что:
Значения максимума и минимума воздушного зазора для рассматриваемого на рис. 1 эксцентриситета ε = 80 % использовались для расчёта аргумента зависимости λК = f(b/δ). Зависимость λК (ε) (показанная на рис. 4 в долях проводимости λК (0) ), рассчитывалась по выражению:
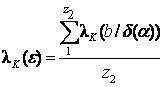 ,
(4)
,
(4)где ![]() –сумма
магнитных проводимостей по коронкам зубцов ротора над каждым
пазом.
–сумма
магнитных проводимостей по коронкам зубцов ротора над каждым
пазом.
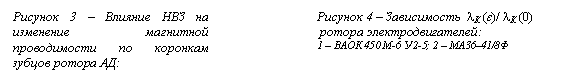 .
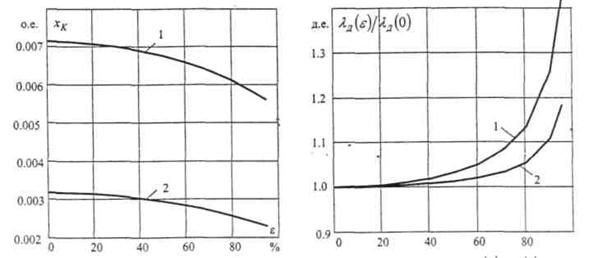
.На рис. 5 приведена зависимость xК (ε), определяемая с использованием
выражения
xК (ε) = KλК (ε)
где K –
коэффициент:
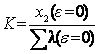 ,
,
Проанализируем влияние НВЗ на изменение магнитной проводимости дифференциального рассеяния АД.
Теоретическое выражение для магнитной проводимости дифференциального
рассеяния ротора имеет следующий вид [2]: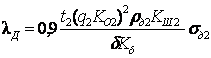 .
.
где KШ2 – коэффициент, зависящий
от отношений открытия паза к пазовому делению t2: 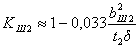 ;
;
ρд2 – коэффициент
демпфирования ротора; q2 – число пазов на полюс и фазу ротора;
KО2 – обмоточный коэффициент, равный при беличьей клетке
единице; Кδδ – коэффициент воздушного зазора: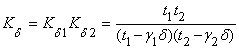 ;
;
σд2 – коэффициент
дифференциального рассеяния ротора, у1, у2 -
коэффициенты, определяемые по [2].
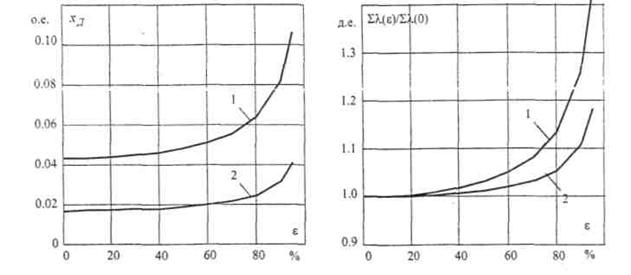
Зависимость магнитной проводимости и индуктивного сопротивления
дифференциального рассеяния от НВЗ, расчитанная по выпажению (5)
(отнесенная к значению λд(0)) и
xК (ε) =
KλК (ε),
приведены на рис. 6, 7.
Результаты расчета электромагнитного параметра двигателей : x'2 (ε) / x'2 (0) = Σλ(ε)/ λ(0) при изменении НВЗ приведены на рис. 8
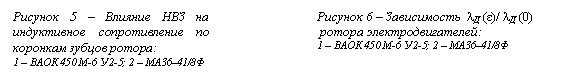 .
.
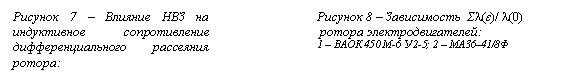 .
.2 Моделирование электромагнитного переходного процесса отключения электродвигателей при НВЗ
Анализ влияния НВЗ на изменение магнитной проводимости воздушного зазора АД. В соответствии с известным выражением для удельной магнитной проводимости воздушного зазора без учета зубчатости статора и ротора, а также явления насыщения
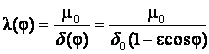 ,
(6)
,
(6)При разложении функции λ(φ) в ряд Фурье с учетом первых двух членов ряда [3, 4]:
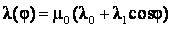 ,
(7)
,
(7)где
 ;
;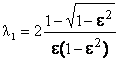 .
. При учете влияния двухсторонней зубчатости на основную гармонику в зазоре АД в работе [3, 4] получено также следующее выражение
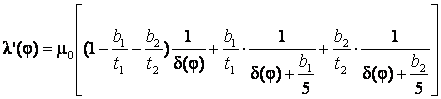 .
(8)
.
(8)Результаты расчета проводимостей без учета зубчатости и с учетом зубчатости статора и ротора при НВЗ, рассчитанные по выражениям (7) и (8) в функции эксцентриситета ряда АД, изображены на рис. 9.
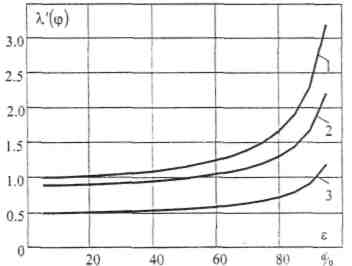
Рисунок 9 – Изменение проводимости воздушного зазора электродвигателей при НВЗ
Из анализа рис. 9 следует, что изменение проводимости воздушного зазора λ'(φ) имеет существенно нелинейный характер, начиная с величины эксцентриситета более 60 %.
Постановка задачи. Для контроля НВЗ асинхронного двигателя возможно использование начального момента отключения двигателя или переходного процесса тока в роторе. В качестве диагностического Сигнала в обоих методических подходах следует использовать изменение магнитной индукции нолей ротора. В указанной связи возникают задачи предопределение изменений электромагнитных параметров асинхронной машины при кратковременном отключении от сети для выбора наиболее информативных диагностических параметров и разработки методики диагностического испытания.
Расчётные условия и уравнение переходного процесса. В начальный момент времени переходного процесса отключения двигателя от сети происходит бросок намагничивающего тока в роторе, вызывающий резкое изменение индукции магнитных полей ротора вблизи вала машины и изменение напряжения на выводах обмотки статора, характеризуемое величиной изменения тока ротора в начальный момент и последующим затуханием с постоянной времени обмотки возбуждения. Последняя характеризует также изменение магнитной индукции полей ротора.
При отключении двигателя, работающего на холостом ходу, скачкообразное изменение напряжения (ЭДС) обмотки статора может определяться по выражению:
где х" – сверхпереходное индуктивное сопротивление
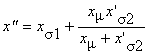 .
(10)
.
(10)E"(0) –сверхпереходная ЭДС
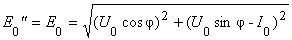 .
.
Изменение напряжения на выводах обмотки статора происходит по закону:
где
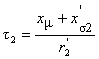 .
.
Изменение магнитной индукции полей ротора после коммутации происходит с
той же постоянной времени:
Из сопоставления выражений для E(t) и B(t) следует, что первая из них
зависит от насыщения пути основного магнитного потока машины и
механической нагрузки на валу агрегата, определяющей закон изменения
ротора ω2 (t).
Как следует из анализа баланса магнитных потоков, в начальный момент
переходного процесса (в системе о.е.):
где Δis0 – изменение тока в обмотке статора, равное его исходному значению I0; ira(0) – бросок намагничивающего тока в обмотке ротора.
Из выражения (12) имеем:
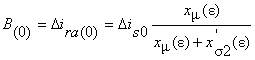 .
(13)
.
(13)Измерение магнитной индукции B(t) может быть реализовано на базе датчика Холла, расположенного вне корпуса двигателя.
Расчёт переходных процессов в обмотке ротора при неравномерном воздушном зазоре. Изменение B(ε,t), отражающее влияние НВЗ, рассчитывалось с использованием выражении, приведенных выше.
Зависимости х'σ2(ε) и хμ(ε) рассчитываемые по
выражениям:
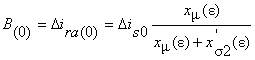 ,
(14)
,
(14) ,
(15)
,
(15)Зависимость х" в функции эксцентриситета ротора, полученная по
выражению (10) на основе данных х'σ2(ε)
и хμ(ε) ,
показана на рис. 12.
Изменение постоянной времени переходных токов в роторе при разомкнутой
обмотке статора τ2–, показано
на рис. 13 в функции
эксцентриситета ротора, а изменение магнитной индукции полей рассеяния –
на рис.14.
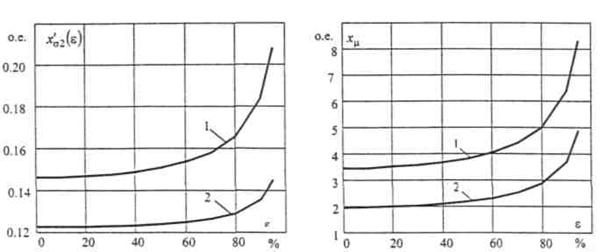

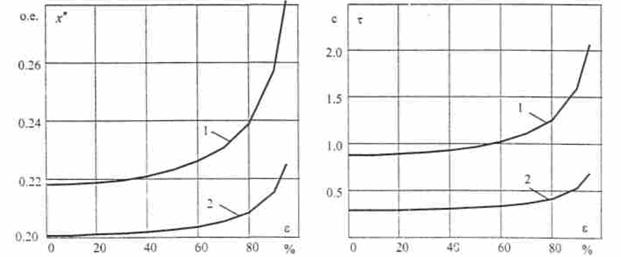

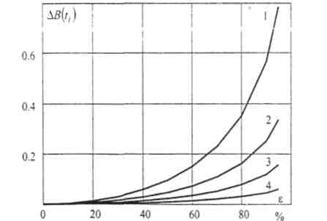
Рисунок 14 – Влияние НВЗ на изменение индукции поля рассеяния ротора при отключении электродвигателя от сети:
1 - t = τ2; 2 - t = 0,5τ2; 3 - t = 0,25τ2; 4 - t = 0,1τ2.
Вывод. Как следует из анализа рис. 14, изменение магнитной индукции полей рассеяния может быть использовано для экспресс–диагностики НВЗ двигателей при ε = 40–50 % в случае регистрации изменения этого диагностического параметра при t = 0 и t = τ2.
Литература:
- Рогозин Г.Г. Контроль равномерности воздушного зазора асинхронной машины по значению синхронного индуктивного сопротивления. – Электричество. 1981 г, № 5. – с. 44–46.
- Сергеев П.С, Виноградов Н.В. Проектирование электрических машин. – М.: Энергия, 1970. – 632 с.
- Никитян Н.Г, Йондем М.Е. Магнитное поле в воздушном зазоре асинхронные машины при натичии эксцентриситета.–Ереван: Издательство ЕПИ., 1983.–14 с.
- Геллер Б., Гамата В. Высшие гармоники в асинхронных машинах.–М.: Энергия,1981.