|
NEURAL NETWORKS .
1. Introduction to neural networks
1.1 What is a Neural Network?
An Artificial Neural Network (ANN) is an information processing paradigm that is inspired by the way biological nervous systems, such as the brain, process information. The key element of this paradigm is the novel structure of the information processing system. It is composed of a large number of highly interconnected processing elements (neurones) working in unison to solve specific problems. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Learning in biological systems involves adjustments to the synaptic connections that exist between the neurones. This is true of ANNs as well.
1.2 Historical background
Neural network simulations appear to be a recent development. However, this field was established before the advent of computers, and has survived at least one major setback and several eras.
Following an initial period of enthusiasm, the field survived a period of frustration and disrepute. During this period when funding and professional support was minimal, important advances were made by relatively few reserchers. These pioneers were able to develop convincing technology which surpassed the limitations identified by Minsky and Papert. Minsky and Papert, published a book (in 1969) in which they summed up a general feeling of frustration (against neural networks) among researchers, and was thus accepted by most without further analysis. Currently, the neural network field enjoys a resurgence of interest and a corresponding increase in funding.
The first artificial neuron was produced in 1943 by the neurophysiologist Warren McCulloch and the logician Walter Pits. But the technology available at that time did not allow them to do too much.
1.3 Why use neural networks?
Neural networks, with their remarkable ability to derive meaning from complicated or imprecise data, can be used to extract patterns and detect trends that are too complex to be noticed by either humans or other computer techniques. A trained neural network can be thought of as an "expert" in the category of information it has been given to analyse. This expert can then be used to provide projections given new situations of interest and answer "what if" questions.
Other advantages include:
1.Adaptive learning: An ability to learn how to do tasks based on the data given for training or initial experience.
2.Self-Organisation: An ANN can create its own organisation or representation of the information it receives during learning time.
3.Real Time Operation: ANN computations may be carried out in parallel, and special hardware devices are being designed and manufactured which take advantage of this capability.
4.Fault Tolerance via Redundant Information Coding: Partial destruction of a network leads to the corresponding degradation of performance. However, some network capabilities may be retained even with major network damage.
1.4 Neural networks versus conventional computers
Neural networks take a different approach to problem solving than that of conventional computers. Conventional computers use an algorithmic approach i.e. the computer follows a set of instructions in order to solve a problem. Unless the specific steps that the computer needs to follow are known the computer cannot solve the problem. That restricts the problem solving capability of conventional computers to problems that we already understand and know how to solve. But computers would be so much more useful if they could do things that we don't exactly know how to do.
Neural networks process information in a similar way the human brain does. The network is composed of a large number of highly interconnected processing elements(neurones) working in parallel to solve a specific problem. Neural networks learn by example. They cannot be programmed to perform a specific task. The examples must be selected carefully otherwise useful time is wasted or even worse the network might be functioning incorrectly. The disadvantage is that because the network finds out how to solve the problem by itself, its operation can be unpredictable.
On the other hand, conventional computers use a cognitive approach to problem solving; the way the problem is to solved must be known and stated in small unambiguous instructions. These instructions are then converted to a high level language program and then into machine code that the computer can understand. These machines are totally predictable; if anything goes wrong is due to a software or hardware fault.
Neural networks and conventional algorithmic computers are not in competition but complement each other. There are tasks are more suited to an algorithmic approach like arithmetic operations and tasks that are more suited to neural networks. Even more, a large number of tasks, require systems that use a combination of the two approaches (normally a conventional computer is used to supervise the neural network) in order to perform at maximum efficiency.
Neural networks do not perform miracles. But if used sensibly they can produce some amazing results.
2. Human and Artificial Neurones - investigating the similarities
2.1 How the Human Brain Learns?
In the human brain, a typical neuron collects signals from others through a host of fine structures called dendrites. The neuron sends out spikes of electrical activity through a long, thin stand known as an axon, which splits into thousands of branches. At the end of each branch, a structure called a synapse converts the activity from the axon into electrical effects that inhibit or excite activity from the axon into electrical effects that inhibit or excite activity in the connected neurones. When a neuron receives excitatory input that is sufficiently large compared with its inhibitory input, it sends a spike of electrical activity down its axon. Learning occurs by changing the effectiveness of the synapses so that the influence of one neuron on another changes.
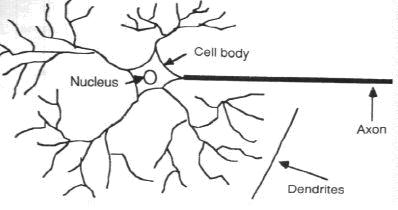
Figure 1 – Components of a neuron
2.2 From Human Neurones to Artificial Neurones
We conduct these neural networks by first trying to deduce the essential features of neurones and their interconnections. We then typically program a computer to simulate these features. However because our knowledge of neurones is incomplete and our computing power is limited, our models are necessarily gross idealisations of real networks of neurones.
3. An engineering approach
3.1 A simple neuron
An artificial neuron is a device with many inputs and one output. The neuron has two modes of operation; the training mode and the using mode. In the training mode, the neuron can be trained to fire (or not), for particular input patterns. In the using mode, when a taught input pattern is detected at the input, its associated output becomes the current output. If the input pattern does not belong in the taught list of input patterns, the firing rule is used to determine whether to fire or not.
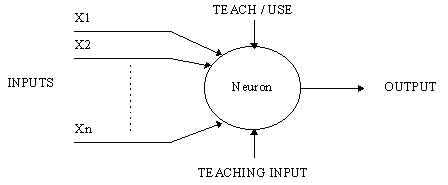
Figure 2 – A simple neuron
3.2 A more complicated neuron
The previous neuron doesn't do anything that conventional conventional computers don't do already. A more sophisticated neuron (figure 1) is the McCulloch and Pitts model (MCP). The difference from the previous model is that the inputs are 'weighted', the effect that each input has at decision making is dependent on the weight of the particular input. The weight of an input is a number which when multiplied with the input gives the weighted input. These weighted inputs are then added together and if they exceed a pre-set threshold value, the neuron fires. In any other case the neuron does not fire.

Figure 3 – An MCP neuron
In mathematical terms, the neuron fires if and only if:
X1W1 + X2W2 + X3W3 + ... > T
The addition of input weights and of the threshold makes this neuron a very flexible and powerful one. The MCP neuron has the ability to adapt to a particular situation by changing its weights and/or threshold. Various algorithms exist that cause the neuron to 'adapt'; the most used ones are the Delta rule and the back error propagation.
|
|