Ковалев А.П., Муха В.П., Джура С.Г., Якимишина В.В., Зрадовская О.Я.
Донецкий национальный технический университет.

Ссылка на первоисточник: Наукові праці Донецького національного технічного університету. Серія: "Елеутротехніка і енергетика", випуск 112: Донецьк: ДонНТУ, 2006. - 154 с.

        On the basis of casual Мarkov processes with the discrete number of the states and the mathematical model of melting of active area of reactor is continuous time offered. The example of calculations is resulted.

        Введение. Известно, что 28 марта 1979 г. в 4 часа утра по местному времени на американской АЭС в Гаррисберге «Три-Майл-Айленд» на реакторе PWR (легководный реактор с водой под давлением) мощностью 885 МВт энергоблока №2 произошла авария [1].

        В результате аварии была расплавлена верхняя часть активной зоны реактора, после чего восстановление его стало нецелесообразно. Общий ущерб от аварии составил 1,86 млрд. долларов [2].

        Под риском (в данном случае при эксплуатации АЭС) будем понимать вероятность наступления с течением времени t=1 год такого случайного события, при котором происходит расплавление активной зоны реактора.

        Согласно рекомендациям МАГАТЭ приемлемый риск широкомасштабного загрязнения радионуклидами окружающей среды в результате аварии на АЭС или на другой ядерной установке не должен превышать вероятность в течение года. Во Франции риск, связанный с эксплуатацией реактора АЭС, признается приемлемым только после того, как будет доказано, что вероятность аварии на нем в течение года не превосходит значения 1^.10^-7 [3].

        Состояние вопроса. Анализ причин, которые привели к аварии на АЭС «Три-Майл-Айленд» [1,2], позволил представить расплавление активной зоны реактора как совпадение в пространстве и времени следующих пяти случайных событий: аварийное отключение питательных насосов; отказ во включении аварийной системы охлаждения активной зоны; отказ разгрузочного клапана компенсатора объема в открытом положении; отказ насосов высокого давления; отказ насосов первого контура.

        Цель работы. Используя понятия Марковских случайных процессов, оценить вероятность расплавления активной зоны реактора в течение года F₁(t), определить среднее время до аварии и дисперсию при условии, что в начальный момент времени все системы обеспечения безопасности АЭС находились в работоспособном состоянии, а также при условии, что обслуживающий персонал не делает ошибок при эксплуатации.

        Материал и результаты исследования. При составлении математической модели, описывающей процесс возникновения аварии на АЭС, принимаем ряд допущений и положений:

        - отказавшее состояние аварийной системы охлаждения, запорной арматуры и различных средств защиты, которые находятся в «ждущем режиме», обнаруживается только в результате профилактических проверок либо после изучения причины аварии обнаруживается отказавшее состояние средств защиты;

        - проверки систем защит, находящихся в «ждущем режиме», абсолютно надежны;

        - после каждого отказа рассматриваемых систем их отказавшее состояние обнаруживается, и работоспособное состояние полностью восстанавливается (система работает как новая);

        - человек при эксплуатации принимает неправильные решения (отказывает) в результате повреждений регистрирующих приборов на пульте управления, по показаниям которых оператор принимает решение.

        Обозначим через k=5 число систем, участвующих в формировании аварии, связанной с расплавлением активной зоны реактора на АЭС.

        Процесс изменения состояния каждой из k рассматриваемых систем с течением времени t обозначим через , . Предположим, что принимает два значения: 0, если k-я система находится в работоспособном состоянии, и 1, если в отказавшем. Что касается статистической природы этих функций, то предположим, что вероятность переходов из работоспособного состояния в неработоспособное за промежуток времени равна , где означает, что вероятность появления более одного отказа в интервале является величиной высшего порядка малости по сравнению с . Вероятность переходов из неработоспособного состояния в работоспособное за время равна и не зависит от предшествующего течения процесса .

        Величины и являются параметрами рассматриваемых процессов. Принятые допущения означают, что можно рассматривать как процесс Маркова с двумя состояниями 0 (работоспособное) и 1 (неработоспособное) [4].

        Рассмотрим совокупность процессов как один процесс Маркова с 32 дискретными состояниями и непрерывным временем. Авария на АЭС с расплавлением активной зоны реактора произойдет в момент встречи процесса в состоянии 1, т.е. когда , , , , .

        Выразим вероятность нахождения системы в каждом из 32 возможных состояний через параметры известных процессов , , , , .

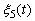        Поведение во времени такой системы полностью определяется матрицей интенсивностей переходов Р, которая для данной задачи примет вид:

,          (1)

        где

.          (2)

        Матрицы и отличаются между собой только элементами главной диагонали. Главная диагональ матрицы начинается элементом , а заканчивается элементом . Диагональные элементы матриц и определяются как единица минус сумма элементов соответствующей строки. Например:

        В матрице (2) ; ; , где

        , - средний интервал времени между отказами питательных насосов и средняя длительность нахождения питательных насосов в отказавшем (нерабочем) состоянии;

        , - средний интервал времени между отказами во включении аварийной системы охлаждения и средняя длительность нахождения аварийной системы охлаждения в отказавшем состоянии;

        , - средний интервал времени между отказами (заклинивание в открытом положении) разгрузочного канала компенсатора объема и средняя длительность нахождения его в отказавшем состоянии;

        , - средний интервал времени между ошибочными отключениями (или выходов из строя) насосов высокого давления и средняя длительность нахождения насосов высокого давления в отключенном (отказавшем) состоянии;

        , - средний интервал времени между ошибочными отключениями (или выходом из строя) насосов первого контура и средняя длительность нахождения их в отключенном (отказавшем) состоянии.

        Вероятность нахождения рассматриваемой системы в каждом из 32 возможных состояний можно найти из решения системы линейных дифференциальных уравнений, записанных в матричном виде:

,          (3)

        где 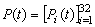- вектор-строка; , где I – единичная матрица; Р- матрица интенсивностей переходов (1).

        Система линейных дифференциальных уравнений (3) должна решаться при начальных условиях:

.

        численным методом с помощью ЭВМ [5]. Вероятность нахождения всех пяти процессов в состоянии (1,1,1,1,1) и будет равна вероятности расплавления активной зоны реактора, т.е.:

,          (4)

        Значение среднего времени до расплавления активной зоны реактора , если в начальный момент времени все k рассматриваемые системы находились в работоспособном состоянии, (оборудование работало в нормальном режиме, люди не делали в процессе эксплуатации реактора ошибок) находим из следующей системы уравнений, записанной в матричном виде:

,          (5)

        где: - фундаментальная матрица;

        Q – матрица, полученная из матрицы интенсивностей переходов (1) за исключением из нее поглощающего состояния (последней строки и последнего столбца);

         – вектор-столбец, у которого все элементы равны единице;

         - вектор-столбец.

        Дисперсия времени до первой аварии, сопровождающейся расплавлением активной зоны реактора, можно определить, пользуясь общей системой уравнений [6]:

,          (6)

        где и - векторы-столбцы.

        Для систем, находящихся в «ждущем режиме» (средства защиты, управление запорной арматурой и т.д.), для которых заданы интервалы времени между профилактиками , параметр потоков обнаружения и устранения выявленного отказа можно находить используя формулу [7]:

,          (7)

        При выполнении условия (свойство экспоненциального распределения), вероятность расплавления активной зоны реактора можно определить из выражения:

.          (8)

        В том случае если:

, , ,          (9)

        тогда используя (1), (2), (5), находим .

,          (10)

        где .

        ПРИМЕР. Определить вероятность расплавления активной зоны реактора в течение года при совпадении в пространстве и времени следующих случайных событий: произошло аварийное отключение питательных насосов; отказала во включении аварийная система охлаждения активной зоны реактора; отказал разгрузочный клапан на компенсаторе объема в открытом состоянии; отказали (отключились) насосы высокого давления; отказали (отключились) циркуляционные насосы первого контура.

        Сравнить полученный результат с нормируемой величиной .

        Дано: ; ; ; ; ; ; ; ; ; .

        Решение. Ввиду того, что в нашем случае соблюдается условие (9), т.е. , следует воспользоваться формулами (4), (8) и (10). Тогда получим:

.

        Сравнение полученного результата с нормой показало, что в данном случае риск расплавления активной зоны реактора в течение года выше нормируемого в 4,85 раза.

Литература.