
Автореферат
Цель и задача: оценить электромагнитную совместимость с использованием квадратичного инерционного сглаживания (КСИ). Показать принципиальную неточность существующего метода расчета по полиномам Чебышева-Эрмита. Проверить возможность использования распределения Джонсона или Пирсона. Оценить погрешность предложенного метода для частный случаев, когда имеется аналитическое решение.
Актуальность вопроса связана с обеспечением условий электромагнитной совместимости (ЭМС). От точности оценивания характеристик процесса после блока КСИ зависит достоверность оценивания ЭМС. Нарушение ЭМС приводит к дополнительным потерям мощности, ущербу.
Введение:
ПОНЯТИЕ ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ
Существуют различные определения электромагнитной совместимости (ЭМС):
- под ЭМС понимается способность электроприемника (приемника) нормально функционировать в окружающей электромагнитной среде и не вносить в эту среду помех, недопустимых для других приемников. Применительно к задачам электроснабжения под электромагнитной средой понимается сеть электроснабжения, к которой подключена группа приемников.
- под ЭМС электроприёмников понимается их свойство функционирования без ухудшения показателей качества электроэнергии при совместном питании от общей электрической сети..
- под ЭМС понимается способность технического средства функционировать с заданным качеством в заданной электромагнитной обстановке и не создавать недопустимых электромагнитных помех другим техническим средствам.
Проблема ЭМС в определенном смысле аналогична проблеме охраны окружающей среды: возрастание мощностей электроприемников и интенсификация режимов их работы приводят к искажению параметров электрической энергии, что, в свою очередь, отрицательно сказывается на режимах работы других электроприемников сети. Обеспечение ЭМС связано со значительными затратами, обусловливающими высокие требования, предъявляемые к точности и обоснованности методов оценки ЭМС в сетях электроснабжения.
Нарушения ЭМС может происходить, как по вине энергоснабжающей организации, так и в следствие работы электроприемников (ЭП) на рассматриваемом предприятии.
В первом случае напряжение источника питания Uи не является чисто синусоидальным, поэтому и напряжение на шинах остальных ЭП Uш также является несинусоидальным (рис. 1).

Рис. 1 - К понятию ЭМС>
Во втором случае источником помех (НН на рис. 1) является ЭП с нелинейной вольтамперной характеристикой (ВАХ), который потребляет несинусоидальный ток (на рис. 1 для простоты силовой трансформатор в системе электроснабжения не показан). Тогда, даже если напряжение источника питания синусоидальное, то несинусоидальный ток создает несинусоидальную потерю напряжения в активном и индуктивном сопротивлениях сети. В результате напряжение на шинах будет несинусоидальным, что будет отрицательно сказываться на работе остальных ЭП.
Для оценивания ЭМС необходимо иметь математическое описание (математическую модель) ЭП и сети. Обычно сеть задается сосредоточенными сопротивлениями r и x . Модели электроприемников выбираются, по возможности, простыми, но отражающими основные свойства ЭП.
Оценку ЭМС можно получить моделированием процессов, вызывающих изменение свойств сети и электроэнергии. В зависимости от принятой модели сети и (или) приёмника, различают статические и динамические показатели ЭМС.
Статические модели применяются в тех случаях, когда помехи не изменяются или изменяются во времени очень медленно. В этих случаях можно пренебречь переходными процессами. Статические модели описываются формулами, связывающими входной и выходной процессы. Любой ординате входного процесса соответствует определенная ордината выходного процесса.
Динамические модели используются при быстроизменяющихся помехах. Эти модели описываются дифференциальными уравнениями, связывающими входной и выходной процессы. Между ординатами входного и выходного процессов функциональная связь отсутствует.
Выбор модели определяется конкретными условиями задачи. Для практических целей приходится применять по возможности простые модели, отражающие основные факторы ЭМС. Большинство задач по оценке ЭМС в электрических системах могут быть решены в рамках энергетической модели в виде входного блока 1 (выпрямителя), фильтра 2 и энергетического блока 3 (рис 2). Фильтр преобразует входной процесс U(t) в процесс , по которому оцениваются воздействия помехи. Динамический показатель ЭМС является параметром выходного процесса , который характеризует энергию процесса . Обычно диапазон изменения помех невелик, поэтому фильтр может быть линеаризирован. В целом энергетическая модель является нелинейной.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ГОСУДАРСТВЕННОГО СТАНДАРТА НА КАЧЕСТВО ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
ГОСТ 13109-97 «Нормы качества электрической энергии в системах электроснабжения общего назначения» (далее ГОСТ) устанавливает показатели и нормы качества электроэнергии в электрических сетях систем электроснабжения общего назначения переменного трехфазного и однофазного тока частотой 50 Гц в точках, к которым присоединяются электрические сети, находящиеся в собственности различных потребителей электрической энергии, или приемники электрической энергии (точки общего присоединения). ГОСТ 13109-97 является межгосударственным стандартом и действует в Российской Федерации с 1 января 1999г.
Нормы КЭ, установленные стандартом, являются уровнями электромагнитной совместимости для кондуктивных электромагнитных помех в системах электроснабжения общего назначения. При соблюдении установленных норм КЭ обеспечивается электромагнитная совместимость электрических сетей энергоснабжающих организаций и электрических сетей потребителей электрической энергии или ЭП.
Стандартом не устанавливаются требования к КЭ в электрических сетях специального назначения (контактных, тяговых, связи), передвижных установок (самолетов, поездов, судов) и др.
Кондуктивная электромагнитная помеха в системе электроснабжения — электромагнитная помеха, распространяющаяся по элементам электрической сети.
Точка общего присоединения — точка электрической сети общего назначения, электрически ближайшая к сетям рассматриваемого потребителя электрической энергии, к которой присоединены или могут быть присоединены электрические сети других потребителей.
Стандартом не устанавливаются нормы КЭ для режимов вызванных форс-мажорными обстоятельствами (исключительными погодными условиями, стихийными бедствиями и др.).
ГОСТ 13109-97 является первым стандартом в области КЭ, где сказано, что установленные нормы подлежат включению в технические условия на присоединение потребителей и в договоры энергоснабжения.
Потребителям, являющимся виновниками ухудшения КЭ, для обеспечения норм стандарта в точках общего присоединения допускается устанавливать в технических условиях на присоединение и в договорах энергоснабжения более жесткие нормы (с меньшими диапазонами изменения соответствующих показателей КЭ), чем установлены в стандарте.
Нормы стандарта должны применяться при проектировании и эксплуатации электрических сетей, при установлении уровней помехоустойчивости ЭП и уровней электромагнитных помех, вносимых этими приемниками в электрическую сеть, к которой они присоединены.
НЕСИНУСОИДАЛЬНОСТЬ НАПРЯЖЕНИЯ
В процессе выработки, преобразования, распределения и потребления электроэнергии имеют место искажения формы синусоидальных токов и напряжений. Источниками искажений являются синхронные генераторы электростанций, силовые трансформаторы, работающие при повышенных значениях магнитной индукции в сердечнике (при повышенном напряжении на их выводах) преобразовательные устройства переменного тока в постоянный и ЭП с нелинейными вольт-амперными характеристиками (или нелинейные нагрузки).
Искажения, создаваемые синхронными генераторами и силовыми трансформаторами, малы и не оказывают существенного влияния на систему электроснабжения и на работу ЭП. Главной причиной искажений являются вентильные преобразователи, электродуговые сталеплавильные и руднотермические печи, установки дуговой и контактной сварки, преобразователи частоты, индукционные печи, ряд электронных технических средств (телевизионные приемники, ПЭВМ), газоразрядные лампы и др. Электронные приемники электроэнергии и газоразрядные лампы создают при своей работе невысокий уровень гармонических искажений на выходе, но общее количество таких ЭП велико.
Из курса математики известно, что любую несинусоидальную функцию ƒ(ωt) (например, см. рис.3), удовлетворяющую условию Дирихле можно представить в виде суммы постоянной величины и бесконечного ряда синусоидальных величин с кратными частотами. Такие синусоидальные составляющие называются гармоническими составляющими или гармониками. Синусоидальная составляющая, период которой равен периоду несинусоидальной периодической величины, называется основной или первой гармоникой. Остальные составляющие синусоиды с частотами со второй по n-ую называют высшими гармониками.

Рис.3 Несинусоидальность напряженя
Несинусоидальность напряжения характеризуется следующими показателями :
— коэффициентом искажения синусоидальности кривой напряжения;
— коэффициентом n-ой гармонической составляющей напряжения.Коэффициент искажения синусоидальности кривой напряжения KU определяется по выражению, %
 (3.7)
(3.7)
где U(n) — действующее значение n-ой гармонической составляющей напряжения, В;
n — порядок гармонической составляющей напряжения,
N — порядок последней из учитываемых гармонических составляющих напряжения, стандартом устанавливается N =40;
U(1) — действующее значение напряжения основной частоты, В.
Допускается определять KU по выражению, %
 (3.8)
(3.8)
где Uном — номинальное напряжение сети, В.
Коэффициент n -ой гармонической составляющей напряжения равен, %
 (3.9)
(3.9)
Для вычисления KU необходимо определить уровень напряжения отдельных гармоник, генерируемых нелинейной нагрузкой.
Фазное напряжение гармоники в расчетной точке сети находят из выражения :
 (3.11)
(3.11)
где I(n) — действующее значение фазного тока n — ой гармоники;
Uнл — напряжение нелинейной нагрузки (если расчетная точка совпадает с точкой присоединения нелинейной нагрузки , то Uнл = Uном );
Uном - номинальное напряжение сети;
Sк - мощность короткого замыкания в точке присоединения нелинейной нагрузки.
Для расчета U(n) необходимо предварительно определить ток соответствующей гармоники, который зависит не только от электрических параметров, но и от вида нелинейной нагрузки.
Нормально допустимые и предельно допустимые значения KU в точке общего присоединения к электрическим сетям с разным номинальным напряжением приведены в таблице 3.1 .
Таблица 3.1 Значения коэффициента искажения синусоидальности кривой напряжения
| Нормально допустимые значения при Uном, кВ |
Предельно допустимые значения при Uном, кВ |
| 0,38 |
6 — 20 |
35 |
110 — 330 |
0,38 |
6 — 20 |
35 |
110 — 330 |
| 8,0 |
5,0 |
4,0 |
2,0 |
12,0 |
8,0 |
6,0 |
3,0 |
НЕСИММЕТРИЯ НАПРЯЖЕНИЯ
Наиболее распространенными источниками несимметрии напряжений в трехфазных системах электроснабжения являются такие потребители электроэнергии, симметричное многофазное исполнение которых или невозможно, или нецелесообразно по технико - экономическим соображениям. К таким установкам относятся индукционные и дуговые электрические печи, тяговые нагрузки железных дорог, выполненные на переменном токе, электросварочные агрегаты, специальные однофазные нагрузки, осветительные установки.
Несимметричные режимы напряжений в электрических сетях имеют место также в аварийных ситуациях - при обрыве фазы или несимметричных коротких замыканиях.
Несимметрия напряжений характеризуется наличием в трехфазной электрической сети напряжений обратной или нулевой последовательностей, значительно меньших по величине соответствующих составляющих напряжения прямой (основной) последовательности.
Несимметрия трехфазной системы напряжений возникает в результате наложения на систему прямой последовательности напряжений системы обратной последовательности, что приводит к изменениям абсолютных значений фазных и междуфазных напряжений (рис.3.4.).

Рис.4 Векторная диаграмма напряжений прямой и обратной последовательности.
Помимо несимметрии, вызываемой напряжением системы обратной последовательности, может возникать несимметрия от наложения на систему прямой последовательности напряжений системы нулевой последовательности. В результате смещения нейтрали трехфазной системы возникает несимметрия фазных напряжений при сохранении симметричной системы междуфазных напряжений (рис.3.5.).

Рис.5 Векторная диаграмма напряжений прямой и нулевой последовательности.
Несимметрия напряжений характеризуется следующими показателями:
— коэффициентом несимметрии напряжений по обратной последовательности;
— коэффициентом несимметрии напряжений по нулевой последовательности.
Коэффициент несимметрии напряжений по обратной последовательности равен, %
 (3.13)
(3.13)
где U2(1) - действующее значение напряжения обратной последовательности основной частоты трехфазной системы напряжений, В;
U1(1) - действующее значение напряжения прямой последовательности основной частоты, В.
Допускается вычислять K2U по выражению, % :
 (3.14)
(3.14)
где Uном.мф - номинальное значение междуфазного напряжения сети, В.
Коэффициент несимметрии напряжений по нулевой последовательности равен, % :
 (3.15)
(3.15)
где U0(1) - действующее значение напряжения нулевой последовательности основной частоты трехфазной системы напряжений, В.
Допускается вычислять K0U по формуле, %
 (3.16)
(3.16)
где Uном.ф - номинальное значение фазного напряжения, В.
Измерение коэффициента несимметрии напряжений по нулевой последовательности проводят в четырехпроводной сети.
Относительная погрешность определения K2U и K0U по формулам (3.15) и (3.16) численно равна значению отклонений напряжения U1(1) от Uном.
Нормально допустимое и предельно допустимое значения коэффициента несимметрии напряжений по обратной последовательности в точке общего присоединения к электрическим сетям равны 2,0 и 4,0 % .
Нормированные значения коэффициента несимметрии напряжений по нулевой последовательности в точке общего присоединения к четырехпроводным электрическим сетям с номинальным напряжением 0,38 кВ также равны 2,0 и 4,0 % .
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПОМЕХИ
Детерминированные помехи делятся на неизменные, периодические и непериодические. Они описываются функциями времени, заданными аналитически, графически и таблично. Периодические помехи могут быть представлены в виде ряда Фурье. Номер гармонической составляющей (гармоники) будем обозначать по-разному: μ - если длительность tц цикла не равна длительности tf=1/f = 0,02с цикла синусоиды частотой f = 50 Гц, угловой частотой  , и n - при tц = tf. В последнем случае помеха и гармоники называются каноническими. Неканонические помехи имеют основную угловую частоту
, и n - при tц = tf. В последнем случае помеха и гармоники называются каноническими. Неканонические помехи имеют основную угловую частоту  .
Комбинированные периодические помехи в пределах длительности общего цикла имеют участок с одним или несколькими циклами канонической помехи. Примером может служить работа источника помех в повторно-кратковременном режиме, когда за время включения tв он создает каноническую помеху, а во время паузы помеха отсутствует. Относительная длительность участка с помехой
.
Комбинированные периодические помехи в пределах длительности общего цикла имеют участок с одним или несколькими циклами канонической помехи. Примером может служить работа источника помех в повторно-кратковременном режиме, когда за время включения tв он создает каноническую помеху, а во время паузы помеха отсутствует. Относительная длительность участка с помехой  называется коэффициентом включения.
В действующих сетях помехи являются случайными. Если ЭМС оценивается по статическим моделям объектов или по осредненным характеристикам помехи за большой промежуток времени (например, срок службы), то для описания помехи достаточно использовать понятие случайной величины.
Практическое применение теории вероятностей возможно потому, что случайные величины имеют неслучайные характеристики. Полной характеристикой случайной величины х является ее вероятностное распределение, которое может быть задано различными способами: интегральными (кумулятивными) вероятностями Еи , функцией распределения F(x), плотностью распределения f(х). Интегральная вероятность есть вероятность выброса за рассматриваемый уровень. В теории электрических нагрузок функция x(Eи) называется упорядоченной диаграммой, которая получается расположением ординат графика помехи за время Tз записи (регистрации) в порядке убывания. Ось времени диаграммы выражается в относительных единицах (о.е.): Eи=t/Тз, а вероятность измеряется в процентах. Ордината функции распределения равна вероятности того, что помеха будет меньше рассматриваемого уровня х. Отсюда следует, что
называется коэффициентом включения.
В действующих сетях помехи являются случайными. Если ЭМС оценивается по статическим моделям объектов или по осредненным характеристикам помехи за большой промежуток времени (например, срок службы), то для описания помехи достаточно использовать понятие случайной величины.
Практическое применение теории вероятностей возможно потому, что случайные величины имеют неслучайные характеристики. Полной характеристикой случайной величины х является ее вероятностное распределение, которое может быть задано различными способами: интегральными (кумулятивными) вероятностями Еи , функцией распределения F(x), плотностью распределения f(х). Интегральная вероятность есть вероятность выброса за рассматриваемый уровень. В теории электрических нагрузок функция x(Eи) называется упорядоченной диаграммой, которая получается расположением ординат графика помехи за время Tз записи (регистрации) в порядке убывания. Ось времени диаграммы выражается в относительных единицах (о.е.): Eи=t/Тз, а вероятность измеряется в процентах. Ордината функции распределения равна вероятности того, что помеха будет меньше рассматриваемого уровня х. Отсюда следует, что
Eи=1-F, F=1-Eи
Плотность распределения

показывает, насколько кучно располагаются ординаты помехи в окрестностях величины х.
Функция или плотность распределения полностью описывают случайную величину. Используются также числовые характеристики случайной величины, которые могут быть вычислены как по процессу x(t), так и по упорядоченной диаграмме. К ним относятся среднее xc и эффективное xэ значения, а также дисперсия

или стандарт  . Дисперсия характеризует отклонения значений случайной величины от ее среднего значения, а квадрат эффективного значения - среднюю мощность процесса.
Вид закона распределения стремятся выбирать из физических соображений. На форму графика помехи влияет большое количество случайных факторов, что дает основание во многих случаях использовать нормальный закон распределения ординат помехи, который полностью характеризуется средним значением и стандартом.
При
. Дисперсия характеризует отклонения значений случайной величины от ее среднего значения, а квадрат эффективного значения - среднюю мощность процесса.
Вид закона распределения стремятся выбирать из физических соображений. На форму графика помехи влияет большое количество случайных факторов, что дает основание во многих случаях использовать нормальный закон распределения ординат помехи, который полностью характеризуется средним значением и стандартом.
При

плотность и закон нормального закона распределения записываются в виде

где Ф*(х) - табулированная функция стандартного нормального распределения с нулевым средним значением и единичным стандартом.
В каждый момент времени совокупность ординат ансамбля реализаций представляет собой случайную величину со своим законом распределения. Степень линейной связи (корреляции) между моментами времени, разделенными интервалом τ, характеризует корреляционная функция (КФ) К(t,t +τ) с аргументом τ. У стационарных процессов законы распределения и КФ К(τ) не зависят от времени. Для нормальных процессов некоррелированность означает независимость ординат, а у процессов с другими законами распределения отсутствие корреляции еще не означает независимость.
С увеличением длительности между ординатами корреляционная связь затухает: монотонно (при отсутствии почти периодической составляющей) или с колебаниями. В первом случае КФ обычно аппроксимируется недифференцируемым выражением

а во втором - недифференцируемым или дифференцируемым выражениями

где α и ω0 - параметры, α*=α/ω0 . Экспоненциальная КФ является частным случаем при ω0=0.
Нормированная КФ

ЗАКЛЮЧЕНИЕ
Универсальная оценка электромагнитной совместимости (ЭМС) осуществляется в рамках динамических моделей, в которых моделируется реакция рецептора на помеху и оценивается её воздействие путём квадратичного инерционного сглаживания КСИ (например, во фликерметре).
Помехи в электрических сетях являются случайными. Для них аналитическое решение нелинейной задачи о КСИ отсутствует.
Существующие методы расчёта инерционного процесса w(t) на выходе блока КСИ в модели ЭМС позволяют вычислить лишь моменты этого процесса. По ним требуется подобрать аналитическое выражение для плотности f(w) вероятностного распределения инерционного процесса. В [1] плотность определялась по четырём моментам с использованием полинома Чебышева-Эрмита. Однако при этом получаются отрицательные значения ординат (рис.6 красная кривая), что противоречит физическому смыслу. В [2] плотность предложено аппроксимировать по двум начальным моментам и границам изменения инерционного процесса, но обычно эти границы не известны.
Идея предлагаемого метода заключается в том, что, как и в методе [1], используются четыре момента распределения, но аппроксимация осуществляется распределениями Джонсона или Пирсона. В этом случае плотность распределения является сугубо положительной, а определение границ распределения не требуется.
Проверка метода была выполнена на примере процессов: периодического, с прямоугольными импульсами и телеграфного сигнала, для которых точное решение известно. Получены приближённые решения для потоков прямоугольных импульсов с различными распределениями длительностей и пауз, а также для нормальных случайных процессов с корреляционными функциями, которые часто встречаются в практике.
Для тех случаев, когда точное решение не известно, оценка точности приближённых решений была выполнена методами имитации случайных помех. С этой целью использовался разработанный в ДонНТУ метод элементных процессов, который заключается в имитации большого количества n импульсных процессов простой формы (прямоугольных, экспоненциальных и др.), корреляционные функции которых одинаковы и в n раз меньше заданной. Сумма этих процессов даёт заданную корреляционную функцию и нормальное распределение суммарного процесса.
Полученные данные позволяют оценивать ЭМС для случайных помех различного вида и оценить ущерб от нарушения ЭМС.
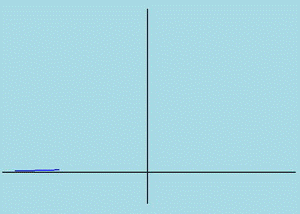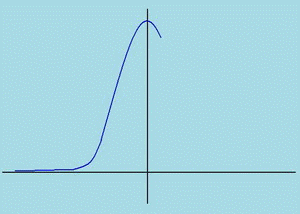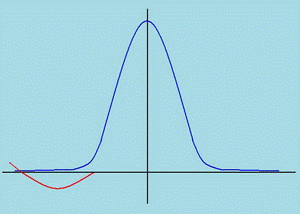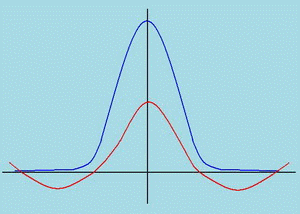
Рис.6 Плотность распределения: кр- по полиномам Чебышева-Эрмита.
син - Джонсона
Перечень ссылок
1. Свешников А.А. Прикладные методы теории случайных функций. – М.: Наука, 1968. – 463с.
2. Kourenny E.G., Petrov V.A., Pogrebnyak N.N. Squaring and smoothing in EMC models: a statistical solution/ 50th International Wroclaw symposium and exhibition: Electromagnetic compatibility 2000. – Wroclaw: National Institute Telecommunications, 2000, part 1. – p. 322-325.