Abstract

The purpose and task: is to appreciate electromagnetic compatibility with use of quadratic inertial smoothing (QIS) and to show basic discrepancy of the existed method of account on polynomials Tchebyshev – Hermite, to check up the opportunity of distribution use Jonsons or Pirsons, to appreciate an error of the offered method for special cases, when there is an analytical decision.

The urgency of a question is connected to maintenance electromagnetic compatibility (EMC) conditions. The reliability appreciate EMC depends on accuracy of process characteristics estimation after the block QIS. The infringement EMC results to additional losses of capacity and damage.

      The universal estimation of electromagnetic compatibility (EMC) is carried out within the dynamic models framework, in which the reaction receptors on the handicap is simulated and estimated its influence by quadratic inertial smoothing QIS (for example, in flicermetre).
      The interferences in electrical networks are occasional. The analytical decision of the nonlinear task about QIS is absent for them.
      The existed methods of process account w (t) on the block output QIS in model EMC allow to calculate only moments of this process. It is required to pick up analytical expression for density f (w) probabilistic of assignment of inertial process according to them. In [1] density was defined on four moments with usage polynomial Tchebyshev - Hermite. However thus the negative values of ordinates (pic. 26 and 27 in [1] and pic. 1-red line) turn out, that contradicts physical sense. In [2] density is offered to approximate on two initial moments and borders of the inertial process change, but usually these borders are not known.
      The idea of the offered method contains that, as well as in the method [1], four moments of distribution are used, but the approximation is carried out by distributions Jonsons or Pirsons. In this case distribution density Jonsons is particularly positive.
      The check of the method was done on example the processes example: periodic, with A-quad-B (rectangular) pulses and telegraphic signal, for which the exact decision is known. The approached decisions for flows of A-quad-B (rectangular) pulses with various distributions durations and pauses have been, and also for normal stochastic processes with correlation functions, which often is met in practice.
      For those cases, when the exact solution is not known, the estimation of the approximate solution accuracy was done by the methods of casual interferences imitation. For this purpose the developed in DonNTU the method of element processes was used, which consists of imitation of the quantity n pulse processes in the simple form (A-quad-B(rectangular), exponential etc.), whose correlation functions are identical and in n of time is less given. The sum of these processes gives the given correlation function and distribution total process normal. The received data allow to estimate EMC for random interference of the various kinds and to estimate damage from infringement EMC.

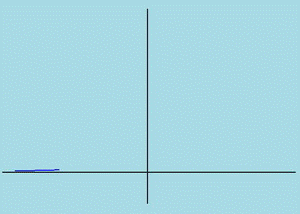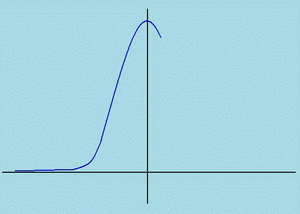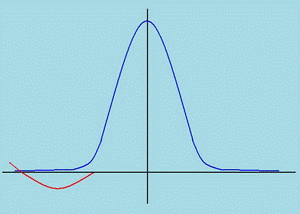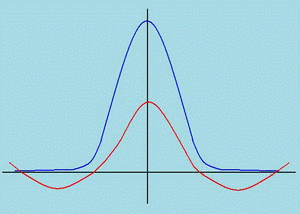
Pic.1 Density of distribution: red - polynomials Tchebyshev – Hermite.
blue - Jonsons

The conclusion

      The task estimation of electromagnetic compatibility with usage of quadratic inertial smoothing has been considered. The basic discrepancy of the existed method of account on Tchebyshev - Hermite has been shown. The density of process after smoothing approximate by curves Jonsons or Pirsons has been offered.

The literature