ББК 31.291
Ч-61
УДК 62-83(075.8)
Чиликин М.Г., Сандлер А.С.
Общий курс электропривода: Учебник для вузов. - 6-е изд., доп. и перераб. - М.: Энергоиздат, 1981. - 576 с., ил.
Стр. 38-40.
2.3. Уравнение движения электропривода
Выше были рассмотрены условия работы электропривода в установив-шемся режиме, когда момент, развиваемый двигателем, равен моменту со-противления механизма и скорость привода является постоянной. Однако во многих случаях привод ускоряется или замедляется, и тогда возникает инер-ционная сила или инерционный момент, которые двигатель должен преодо-левать, находясь в переходном режиме. Таким образом, переходным режи-мом электропривода называют режим работы при переходе от одного уста-новившегося состояния к другому, когда изменяются скорость, момент и ток.
Причинами возникновения переходных режимов в электроприводах яв-ляется либо изменение нагрузки, связанное с производственным процессом, либо воздействие на электропривод при управлении им, т. е. пуск, торможение, изменение направления вращения и т. п. Переходные режимы в электро-приводах могут возникнуть также в результате аварий или нарушения нор-мальных условий электроснабжения (например, изменения напряжения или частоты сети, несимметрия напряжения и т. п.).
Уравнение движения электропривода должно учитывать все силы и мо-менты, действующие в переходных режимах.
При поступательном движении движущая сила F всегда уравновешива-ется силой сопротивления машины Fc и
инерционной силой
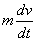 ,
возникающей при изменениях скорости.
Если масса тела m выражена в килограммах, а скорость v — в метрах в секунду, то сила инерции, как и другие силы, действующие в рабо-чей машине, измеряются в ньютонах (кг•м•с-2).
,
возникающей при изменениях скорости.
Если масса тела m выражена в килограммах, а скорость v — в метрах в секунду, то сила инерции, как и другие силы, действующие в рабо-чей машине, измеряются в ньютонах (кг•м•с-2).
В соответствии с изложенным, уравнение равновесия сил при поступа-тельном движении записывается так:
 (2.22)
(2.22)
Аналогично уравнение равновесия моментов, Н•м, для вращательного движения (уравнение движения привода) имеет следующий вид:
 (2.23)
(2.23)
Уравнение (2.23) показывает, что развиваемый двигателем вращающий момент М уравновешивается моментом сопротивления Mс на его валу и инерционным или динамическим моментом 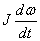 . В (2.22) и (2.23) принято, что масса тела m и соответственно момент инерции привода J являются по-стоянными, что справедливо для значительного числа производственных механизмов. Из анализа (2.23) видно:
. В (2.22) и (2.23) принято, что масса тела m и соответственно момент инерции привода J являются по-стоянными, что справедливо для значительного числа производственных механизмов. Из анализа (2.23) видно:
1) при М > Мс  > 0, т. е. имеет место ускорение привода;
> 0, т. е. имеет место ускорение привода;
2) при М< Мс  <0, т. е. имеет место замедление привода (очевидно, что замедление привода может быть и при отрицательном значении момента двигателя);
<0, т. е. имеет место замедление привода (очевидно, что замедление привода может быть и при отрицательном значении момента двигателя);
3) при М = Мс  = 0; в данном случае привод работает в установив-шемся режиме.
= 0; в данном случае привод работает в установив-шемся режиме.
Вращающий момент, развиваемый двигателем при работе, принимается положительным, если он направлен в сторону движения привода. Если он направлен в сторону обратную движению, то он считается отрицательным.
Отметим, что знак минус перед Мс указывает на тормозящее действие момента сопротивления, что отвечает усилию резания, потерям трения, подъему груза, сжатию пружины и т. п. при положительном знаке скорости.
При спуске груза, раскручивании или разжатии пружины и т. п. перед Мс ставится знак плюс, поскольку в этих случаях момент сопротивления помо-гает вращению привода.
Инерционный (динамический) момент (правая часть уравнения момен-тов) проявляется только во время переходных режимов, когда изменяется скорость привода. При ускорении привода этот момент направлен против движения, а при торможении он поддерживает движение. Инерционный мо-мент как по значению, так и по знаку определяется алгебраической суммой моментов двигателя и момента сопротивления.
При учете сказанного о знаках моментов формула (2.23) соответствует работе двигателя в двигательном режиме при реактивном моменте сопротив-ления (или при потенциальном тормозящем моменте сопротивления). В об-щем виде уравнение движения привода может быть записано следующим об-разом:
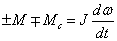 (2.23a)
(2.23a)
Выбор знаков перед значениями моментов в (2.23а) зависит от режима работы двигателя и характера моментов сопротивления.