ББК 31.291
Ч-61
УДК 62-83(075.8)
Чиликин М.Г., Сандлер А.С.
Общий курс электропривода: Учебник для вузов. - 6-е изд., доп. и перераб. - М.: Энергоиздат, 1981. - 576 с., ил.
Стр. 42-44.
2.5. Время ускорения и замедления привода. Определение наивыгоднейшего передаточного отношения
Время переходных режимов привода: пуска, торможения, перехода от одной скорости к другой влияет на производительность механизма. Определение времени переходных процессов основано на интегрировании уравнения движения привода (2.23). Разделяя переменные, получаем:
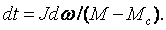 (2.31)
(2.31)
Время, необходимое для изменения скорости привода от
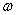 1 до
1 до
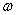 2,
2,
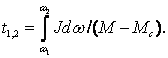 (2.32)
(2.32)
Для решения этого интеграла необходимо знать зависимости моментов двигателя и механизма от скорости. В простейшем случае, приняв М = const, Mc = const и J = const, получим:
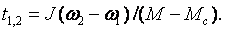 (2.33)
(2.33)
Этим уравнением можно воспользоваться, например, для расчета времени пуска привода. Если значение момента двигателя во время пуска обозначить через Мп, как это показано на рис. 2.10, то получим следующее выражение для времени пуска от состояния покоя до конечной скорости
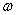 ном, соответствующей заданному моменту сопротивления:
ном, соответствующей заданному моменту сопротивления:
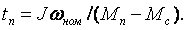 (2.34)
(2.34)
Если требуется точно учесть время переходного процесса и момент двигателя не может быть принят постоянным, например при пуске двигателя с короткозамкнутым ротором, необходимо пользоваться (2.32). При этом следует иметь в виду, что момент инерции для большинства приводов имеет постоянное значение, а момент двигателя и момент сопротивления в переходных режимах обычно не остаются постоянными.
Из (2.32) видно, что теоретически полное время переходного процесса равно бесконечности. Действительно, поскольку переходный процесс заканчивается при наступлении равенства моментов (М = Мс), то величина, стоящая под знаком интеграла, стремится к бесконечности. В практических расчетах обычно считают, что процесс разбега заканчивается при скорости, равной не
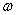 2, а приблизительно
2, а приблизительно
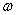 = 0,95
= 0,95
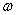 2, тогда время разбега получит конечное значение.
2, тогда время разбега получит конечное значение.

Рис. 2.10. Пусковой график привода.

Рис. 2.11. График торможения привода.
В тех случаях, когда динамический момент имеет отрицательное значение, привод замедляется. Как указывалось выше, для такого случая уравнение моментов будет иметь вид:
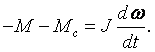
Очевидно, привод замедляется и в том случае, когда двигатель развивает положительный момент по абсолютному значению, меньший момента сопротивления.
Из последнего уравнения следует, что время торможения
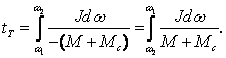 (2.35)
(2.35)
Полагая в частном случае J = const, М = const и Мс = const, получаем:
 (2.36)
(2.36)
Пользуясь уравнением (2.36), можно рассчитать время торможения (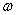 2 = 0) для графика момента, показанного на рис. 2.11.
2 = 0) для графика момента, показанного на рис. 2.11.
Если момент двигателя и момент статический находятся в сложной зависимости от скорости, уравнение движения аналитически не решается. В этом случае приходится пользоваться приближенными графическими или графоаналитическими методами решения.
В ряде практических случаев (например, в следящих системах, приводах вспомогательных механизмов прокатных станов, продольно-строгальных станках и т. п.) возникает необходимость в получении минимального времени разгона и торможения производственного механизма с целью повышения его производительности. При заданных значениях моментов инерции ротора двигателя Jд, производственного механизма Jс и момента сопротивления Мс уравнение движения привода относительно рабочего вала механизма (пренебрегая потерями в передачах) может быть записано так:
 (2.37)
(2.37)
где k — коэффициент, учитывающий момент инерции передач.
Очевидно, минимум времени разгона имеет место при наибольшем ускорении. Из (2.37)

Пользуясь правилом определения максимума d
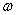 c /dt и полагая Мс — const, а также М — const (средним за период переходного режима), находим оптимальное (или наивыгоднейшее) передаточное отношение i:
c /dt и полагая Мс — const, а также М — const (средним за период переходного режима), находим оптимальное (или наивыгоднейшее) передаточное отношение i:
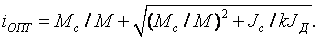 (2.38)
(2.38)
В том случае, когда момент сопротивления оказывается значительно меньшим момента двигателя при пуске и торможении,
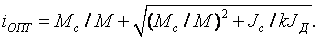 (2.39)
(2.39)