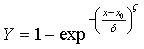 (2)
(2)Максимизация выхода через оптимизацию степеней переработки угля
А.И.А. Салама
Сборник докладов XV Международного конгресса и выставки по обогащению угля. - Китай, 2007. - 928 с.
Назад в библиотеку
Канадский центр минеральных и энергетических технологий (КАНМЭТ)
КАНМЭТ Центр энерготехнологий - Девон
Природные ресурсы Канады
Реферат
В угле смешивание и гомогенизация (усреднение), моделирование процессов переработки угля используется в оптимизации схем для максимизации выхода продуктов обогащения. Переработка разных марок угля или угля разного размера в параллельных схемах и усреднение исходного (угольного) сырья, следующего в процесс, принимается во внимание. В параллельных схемах переработки целью является оптимизация степени переработки угля для достижения максимального выхода с заданным содержанием золы. Смешивание переработанных углей с рядовым также учитывается. В усреднении рядового угля целью является оптимизация процесса смешивания для достижения максимального выхода продуктов с заданным содержанием золы. В моделировании используется две функции, одна изначально основана на физико-химическом составе угля, а вторая является вариацией простой функции Вейбулла. Обе функции эффективнее, чем полиномиальные функции, предложенные в литературе. Предложенные техники напрямую могут применяться инженерами заводов. Использовано несколько иллюстраций для демонстрации предложенных техник.
Введение
Усреднение угля используется для уменьшения разброса в качественных характеристиках исходного питания (сырья) завода (фабрики) и конечных продуктов, и для увеличения выхода в процессе разделения. Широкое варьирование качественных характеристик питания может вызвать различные эффекты в операциях разных частей переработки и будет являться результатом слабого оснащения завода (фабрики). Сглаживание колебаний в количестве материала для переработки может увеличить среднюю нагрузку на перерабатывающее оборудование и упростить операции. Питание, однако, должно быть усреднено правильно. Усреднение после переработки является средством создания продукта, который соответствует требованиям клиента и техническим условиям. Кроме того, усреднение как перед, так и после переработки может уменьшить нежелательный разброс в качественных характеристиках, который не может быть исправлен механически, напр. содержание летучих веществ. В дальнейшем готовые и очень экономные средства по улучшению качества углей для сжигания или для превращения в синтетические топлива достигаются благодаря пользе от смешивания угля.[1]
В случае параллельных схем, используемых для переработки разных марок углей или угля разного размера, степень переработки угля (т.е. точка выхода схемы) может быть оптимально настроена для максимизации общего выхода продуктов, одновременно соответствуя заданному качеству [2, 3, 4, 5]. В 10й МКОУ Салама [4] рассмотрел эту проблему, и были предложены графические техники для ее решения. Естественно, использование графических техник ограничено в обработке маленького числа углей. Другой исследователь рассмотрел более общую проблему смешивания, где характеристики угля определяют через плотность и размер диапазонов, и сформулировал математическую программную проблему [6].
В литературе было предложено смоделировать отношение между суммарной массой (М) и суммарной золой (А) проб угля, используя полиномы [7, 8]. Хорошо известно, что полиномиальная регрессия генерирует ошибочные значения, особенно, когда существует размах в данных. Для иллюстрации этого положения позвольте нам рассмотреть два угля и, используя 5 степень полиномиальной аппроксимация (регрессии) отношения М и А, представить результаты на рис. 1. Ясно, что полиномиальная регрессия генерирует промежуточные значения большие, чем 100%. Также другие полиномиальные регрессии генерируют подобные нереальные результаты. Следовательно, нереальные результаты обеспечивают мотивацию для представления (презентации) данной работы.(…)
Максимизация выхода в параллельных схемах переработки
Давайте рассмотрим смешивание партии углей и каждую характеристику угля подвергнем нелинейной регрессии, используя модели, выраженные через уравнения 1 и 3.M = (A - β)γ/(AS - β)γ (1)
Простая функция Вейбулла выражается как: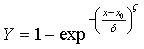 (2)
(2)
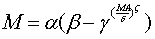 (3)
(3)
Выбранные модели обеспечивают непрерывное отношение между входными (А или [МА]) величинами и выходными (Y или М) величинами. Нелинейная регрессия осуществляет использование "Solver" внутри Microsoft Excelтм для определения оптимальных параметров модели для каждого угля. Результаты нелинейной регрессии используются в следующей проблеме оптимизации. Найдем оптимальное множество, Мi и [МА]i, i = 1, 2, …, N, такое, что общий выход, Y или М, переработанной угольной смеси:
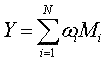 (4)
(4)
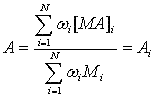 (5)
(5)
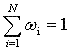 (6)
(6)
Эта проблема оптимизации может быть решена с использованием "Solver" внутри Microsoft Excelтм. Заметим, что коэффициент готовности модуля "Solver" является преимуществом для представления техник.
Представленная оптимизационная проблема может быть упрощенно расширена, чтобы включить смешивание переработанного и рядового угля. В таких случаях каждый рядовой уголь задается одной точкой на оси [МА] и его координаты (Аr, 1), где Аr - общая зола рядового угля.
Полученные результаты применимы для теоретической сепарации, т.е. отсутствие потерь материала с продуктом и бракованными потоками. Однако, если другая псевдо М-кривая, полученная с использованием действительной сепарации каждой пробы угля, то полученные результаты могут применяться с использованием псевдо М-кривых. Стоит заметить, что конечные точки псевдо М-кривой и теоретической М-кривой зафиксированы.
Максимизация выхода в угольном усреднении
В угольном усреднении приращение массы рядовых углей добавляют к каждому интервалу плотности или фракции для генерации данных об угольной смеси. Итоговая угольная смесь подвергается нелинейной регрессии с использованием уравнений моделей 1 и 3, и получаем непрерывное соотношение между входными (А или [МА]) величинами и выходной М величиной. Результаты нелинейной регрессии различных углей используются в оптимизации схем, определенных как: нахождение оптимума М и [МА] такого, что общий выход смеси рядового угля максимизирует предмет с заданным содержанием золы.(…)
Иллюстрации
Случай 1 - смесь двух обогащенных углей. Используется функция физико-химической модели. Зададимся общей зольностью 15%, a итоговые данные и результаты максимизации выхода показаны на рис. 1.
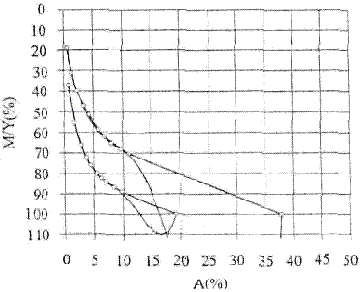
Рис. 1 - Моделирование М-кривых с использованием полиномиальной функции
Случай 2 исключает физико-химическую модель, заменяя ее простой функцией Вейбулла. Отметим, что эта функция имеет пять параметров. Зададимся общей зольностью 18%, a итоговые данные и результаты максимизации выхода показаны на рис. 2.
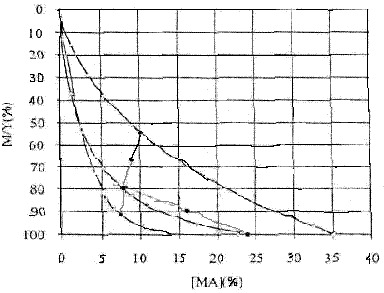
Рис. 2 - Оптимизация выхода с использованием смешивания трех обогащенных углей с рядовым углем - моделирование функцией Вейбулла
(…)
Выводы
Физико-химические свойства угля используются для моделирования характеристик угля, а именно, М-кривых. Более того, благодаря ее желаемым чертам, простая функция Вейбулла также предложена для моделирования М-кривых. Обе функции были признаны очень эффективными в моделировании М-кривых (т.е. обогащение угля).
В случае параллельных схем, использующих в переработке разные марки и разные размеры угля, степень переработки угля (т.е. точка выхода продукта из схемы или операционная точка вдоль М-кривой) оптимально изменяется для определения максимального общего выхода продуктов, пока получается соответствующая заданной зольность. После моделирования различных углей проблема оптимизации смешивания является неограниченной для любого числа углей. Результаты были расширены на смешивание обогащенных углей с рядовыми. Более того, максимизация выхода в переработке смеси рядовых углей (гомогенизация рядового угля) также рассмотрена. Полученные результаты применимы для теоретической сепарации, т.е. без потери материала с продуктами и бракованными потоками. Однако, если другая псевдо М-кривая, полученная с использованием действительной сепарации каждой пробы угля, то предложенные в данной статье результаты могут применяться с использованием псевдо М-кривых. Стоит заметить, что конечные точки псевдо М-кривой и теоретической М-кривой зафиксированы.
Моделирование (Регрессия) и проблемы максимизации выхода решены с использованием модуля "Solver" внутри приложения Microsoft Excelтм, который делает легким его использование для инженеров угольных фабрик. Практические данные использованы для иллюстрации предложенных техник.
Данные схемы оптимизации предложены инженерам-обогатителям с облегчающими использование средствами для максимизации общего выхода в угольном смешивании и гомогенизации.
Назад в библиотеку