Инженеры А. В. Коваль,А. С. Овсянников, И. А. Шпакунов (ИГТМ АН УССР)

 

О ЖЕСТКОСТИ  КОНВЕЙЕРНОЙ  ЛЕНТЫ  ПРИ   ИЗГИБЕ

 

,: сборник статей «Вопросы рудничного транспорта»,

вып. 11, М. «Недра», 1970, 77 – 80

 

Для расчета расстояния между роликоопорами, напряжений в ленте от изгиба при прохождении ленты через барабан и ролики, а также для построения переходных кривых в местах перелома вогнутого профиля конвейера с минимально возможным радиусом необходимо знать цилиндрическую (изгибную) жесткость ленты.

В работах [1, 2, 3] цилиндрическая жесткость ленты (лента рассматривается как однородное изотропное тело) определяется по следующей формуле:

                                                                                                         (1)

где      – жесткость ленты на растяжение (кГ/см прокладки);

  – количество основных прокладок;

  – толщина ленты;

  – коэффициент Пуассона.

Однако практически цилиндрическая жесткость ленты значи­тельно меньше, чем жесткость, определяемая формулой (1). Об этом свидетельствует следующий эксперимент, проведенный Н. Я. Биличенко [4]. К ленте, перекинутой через барабан, при­кладывались растягивающие усилия до разрыва ленты. Оказалось, что усилия разрыва ленты в этом случае отличаются незначи­тельно от усилий разрыва при растяжении без изгиба. Эти экспе­рименты свидетельствуют о весьма малых напряжениях от изгиба ленты по сравнению с растягивающими напряжениями.

Для подтверждения этого положения нами были проведены эксперименты по определению цилиндрической жесткости ленты.

Наиболее просто цилиндрическую жесткость можно определить при чистом изгибе образца. С этой целью был изготовлен стенд (рис. 1), позволяющий определить перемещение в центре иссле­дуемого образца при чистом изгибе.

Из ленты вырезают пластинку шириной b и длиной l. По краю  пластинка свободно оперта, а края   свободны.

 

 

 

 

 

 

 

 

 

 

 

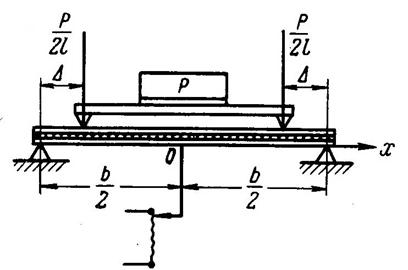
Рис. 1 – Схема   стенда  для  определения цилиндрической  жесткости  ленты

Пластина находится под действием не изменяющейся по длине нормальной нагрузки, приложенной на расстоянии  от опор.

Выбираем  таким образом, чтобы величина . В этом случае можно считать, что пластина изгибается моментами:

                                                                                                        (2)

равномерно распределенными по опертым краям.

Уравнение кривой прогибов при определенном соотношении  для элементарной полоски представим в следующем виде:

                                                                                                             (3)

Граничные условия:

                                                                                                         (4)

Решение уравнения (3), удовлетворяющее граничным условиям (4), будет:

                                                

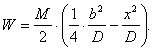
Используя  (2), получим    выражение    для    прогиба в центре пластины:

                                                                                                              (5)

Определив экспериментально прогиб  в центре и зная уси­лие  и геометрические размеры образца ленты из формулы (5), находим цилиндрическую жесткость пластин:

                                                                                                     (6)

 

Для того чтобы исключить влияние свободных краев, были замерены прогибы пластины при различных соотношениях между ее длиной и шириной.

Результаты приведены на рис. 2. Как видно из полученной за­висимости, при <0,9 (=150 мм; =135 мм; =30 кГ) сказы­вается влияние свободных краев. Поэтому при проведении экспе­риментов можно принимать .

 

 

 

 

 

 

 

 

 

 

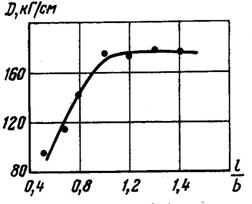
Рис. 2. Зависимость цилиндри­ческой  жесткости пластины от отношения между ее длиной и шириной

Литература:

1. Андреев А. В. Исследование и расчет конвейерных лент и приводе М., Углетехиздат, 1959.

2. Яковлев П. В. Расчет прорезиненных лент с учетом напряжений изгиба. В сб. «Материалы научно-технического совещания по ленточным конвейерам». М., ЦИТИ угля, Госгортехиздат, 1961.

3. Яковлев П. В. Закономерности изменения модуля упругости прорезиненных конвейерных лент и влияние его на напряжения изгиба. Изв. вузе «Горный журнал», 1959, № 7.

 4. Биличенко Н. Я., Высочин Е. М., Завгородний Е. Эксплуатационные режимы ленточных конвейеров. Киев, Гостехиздат, 1964.