МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСПРОСТРАНЕНИЯ МЕТАНА В ТУПИКОВОЙ ВЫРАБОТКЕ ШАХТЫ
Гавриленко Б.В., канд. техн. наук, доц.; Новикова К.Е., магистрант
Предложена математическая модель распространения метана в тупиковой выработке шахты позволяющая проанализировать режимы работы проветривания и аппаратуры газовой защиты при внезапных газодинамических явлениях.
The mathematical model (ММ) of distribution of methane is offered in the blind-alley making of mine allowing to analyse the modes of operations of ventilation.
Наукові праці Донецького національного технічного університету. Випуск 12(113), серія: гірничо-електромеханічна.- Донецьк: ДонНТУ,2006.-344с. с.42
Проблема и ее связь с научными и практическими задачами.
Основная особенность тупиковых (подготовительных) выработок - повышенная вероятность их загазирования и, следовательно, образования взрывчатой метано- воздушной среды. В связи с повышением нагрузки на очистные забои в угольных шахтах увеличиваются темпы проведения и протяженность подготовительных выработок в условиях нарастающей метанообильности и запыленности горных выработок. А.А. Мясников указывает, что метанообильность подготовительных выработок в ряде бассейнов составляет 15 - 20 м3/мин [1]. Вместе с тем подготовительные выработки проветриваются не за счет общешахтной депрессии, создаваемой вентиляторами главного проветривания (ВГП) со 100%-ным резервом по вентиляторным установкам и системам их питания, а вентиляторами местного проветривания (ВМП) в большинстве случаев без такого резервирования. ВМП подвержены частым остановкам из-за срабатывания электрических защит в их системе электроснабжения, нарушений питания и др. Таким образом, вопрос оценки эффективной работы аппаратуры газовой защиты (АГЗ ) является актуальным в настоящее время. Существующие методы не позволяют правильно оценить работоспособность АГЗ поскольку не учитывают динамику распространения метана по тупиковой выработке.
Анализ исследований и публикаций.
Решение задачи моделирования распространения метана в тупиковой выработке шахты приведено в [1]. Однако данная методика обладает рядом существенных недостатков. Во-первых, в данной методике предложено описывать нарастание метана в виде квадратичной зависимости. Такое представление обладает простотой математического описания, но, вместе с тем, имеет недостаточную точность (погрешность достигает 10%). Во-вторых, методика [1] не позволяет получить количественную оценку динамики концентрации метана в тупиковой выработке. Эта динамика необходима для оценки времени срабатывания АГЗ.
Постановка задачи.
Целью данной работы является разработка математической модели (ММ) распространения метана в тупиковой выработке шахты. Данная ММ должна адекватно учитывать динамику изменения концентрации метана в тупиковой выработке, а также определять параметры концентрации метана в любой точке выработки. Реализация такой ММ позволит провести анализ режимов работы аппаратуры газового контроля с точки зрения эффективности и надежности, выявлять особенности протекания опасных газодинамических процессов, приводящих к взрывам метановоздушной смеси.
Изложение материала и результаты.
Исходным уравнением описывающем изменение концентрации метана в выработке является [1]
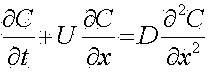
Проветривание выработки происходит под действием турбулентной диффузии. При этом изменение концентрации происходит согласно выражению [2]
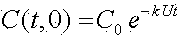
Начальным условием будет
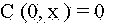
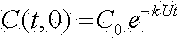
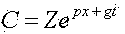
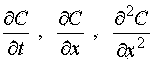
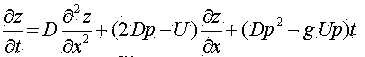
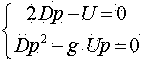
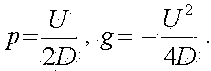
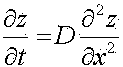
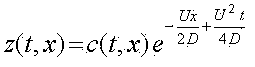
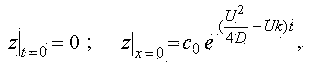
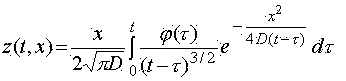
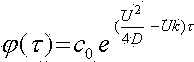
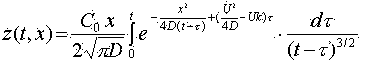
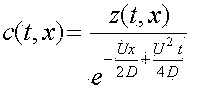

Из полученных расчетов зависимости скорости нарастания и распространения концентрации метана (рис.2 и рис.3)

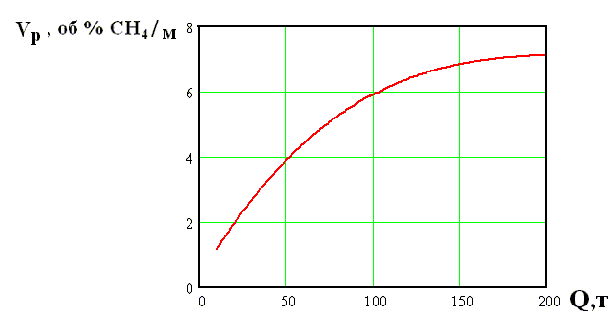
Выводы и направление дальнейших исследований
По результатам данной работы можно сделать следующие выводы:
- Разработана и реализована в виде компьютерной программы ММ распространения метана в тупиковой выработке шахты, позволяющая определять распределение концентрации метана по длине выработки, её изменение во времени , скорости нарастания и распространения концентрации метана.
- C помощью разработанной программы получены зависимости скорости нарастания и распространения концентрации метана от количества выброшенного угля при внезапном выбросе, что позволяет выбирать более эффективные средства газового контроля концентрации метана для безопасного применения электрооборудования в тупиковых выработках.
Список источников.
- Мясников А. А., Казаков С. П. Проветривание подготовительных выработок при проходке комбайнами. - М.: Недра, 1981 г.-269 с. C. 137-141.
- Воронин В.Н. Основы рудничной аэрогазодинамики. М., Углетехиздат, 1951. -315 с. С. 82-96.
- Пигида Г.Л. Элементы теории автоматической газовой защиты очистных участков угольных шахт, М., Недра, 1985, - 189с.
