ИССЛЕДОВАНИЕ НАГРЕВА ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ ТЕРМОКАТАЛИТИЧЕСКИХ ДАТЧИКОВ МЕТАНА
Новикова К.Е., студентка
( Донецкий национальный технический университет, Украина)

Автоматизація технологічних об’єктів та процесів. Пошук молодих. Збірник наукових праць 3-ї Міжнародної науково-технічної конференції аспірантів та студентів в м. Донецьку 14–15. 05. 2003 р.- Донецьк, ДонНТУ, 2003 – 473 с. с.261


Теплофизическая модель. Используется одномерная модель т.е. температура проводника T считается неизменной по сечению . Принято, что форма проволоки идеально цилиндрическая и неизменна в течение процесса. Учитывается зависимость теплофизических свойств материала от температуры. Нагрев проволоки происходит за счет джоулева тепловыделения .
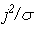Сброс теплоты идет за счет следующих процессов:
1. Естественная конвекция. Процесс считается квазистационарным; не учитываются потоки теплоты в воздухе в направлении вдоль проволоки, вызываемые неравномерностью температуры по ее длине - то есть для расчета теплоотдачи с малого участка длины используется модель бесконечно длинного цилиндра . Тогда тепловой поток с поверхности проволоки q:

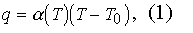
где для определения 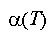используется формула М.А. Михеева, дающая наибольшее значение a для переходного от пленочного (псевдотеплопроводность) к ламинарному режиму течения, характерному для охлаждения тонких проволочек на воздухе

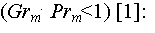
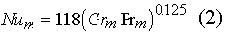
Значения безразмерных критериев берутся при температуре 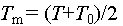. Подставив в (2) выражения для них , и введя 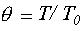, получим:

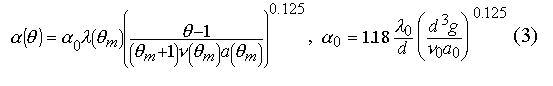
Где 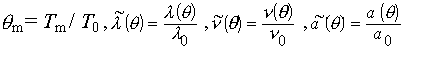- соответственно теплопроводность, кинематическая вязкость и температуропроводность воздуха, отнесенные к своим значениям при Т = T0.
2. Излучение. Тепловой поток определяется по закону Стефана-Больцмана:

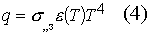
где 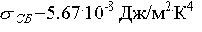- постоянная Стефана-Больцмана, e(T) - степень черноты чувствительного элемента (ЧЭ). Воздух считается диатермичной средой.
3. Теплопроводность. Учитывается , что, потоки теплоты и заряда должны быть связанны друг с другом , так как и теплота и заряд в металле переносятся свободными электронами. Эта связь описывается уравнениями, получаемыми в общей теории переноса (из решения кинетического уравнения) [2]:

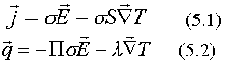
Здесь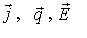- плотность тока, тепловой поток и напряженность поля в проводнике; 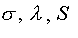- проводимость, теплопроводность и абсолютная термоэдс (коэффициент термо-ЭДС) материала проводника (П = ST - коэффициент Пельтье ). Формула (5.2) показывает, что теплота передается как за счет теплопроводности, так и за счет " макроскопического" движения электронного газа - аналог вынужденной конвекции в "обычном" газе или жидкости. Оценка показывает , что тепловой поток за счет электронной конвекции при 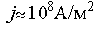может составлять 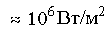, что сравнимо с теплопроводностным потоком 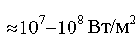, в данном случае, как показал расчет, до 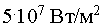, поэтому его, по видимому, необходимо учитывать.
Для этого выразим из (5.1) и подставив в (5.2) получим:

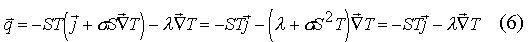
Последнее равенство в (6) записано с учетом того, что величина 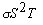, которая учитывает перенос теплоты током, возникающим под действием данного градиента температур (а не под действием внешнего поля) 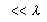, вследствие малости термоэдс 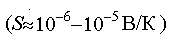. Уравнение (6) представляет собой закон Био-Фурье с поправкой на "электронную конвекцию".
Для определения поля температуры в проволоке T(x,t) запишем с учетом (1), (4) и (6) уравнение теплопроводности и граничные условия к нему:

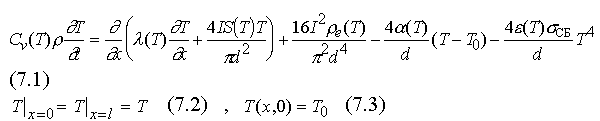
(теплотдача с поверхности приведена к объемным стокам тепла). Здесь Сv- удельная теплоемкость платины, r - плотность, re- удельное электрическое сопротивление, l - теплопроводность, e - степень черноты, I - сила тока в проводнике. Координата x направлена вдоль проводника по току.
Электротехническая модель. Для определения зависимости силы тока в проводнике I от напряжения на его концах U можно пользоваться законом Ома. Для этого воспользуемся (5.1), спроецировав его предварительно на направление проводника s, выразив через него 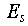, умножив обе части полученного равенства на площадь проводника 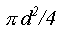(без нарушения общности ее можно считать постоянной по длине) и проинтегрировав по длине проводника l с учетом условия неразрывности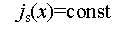

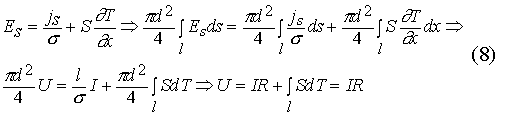
где R- полное сопротивление проводника. Последний интеграл в (8) равен нулю, если температуры обоих концов проводника равны. Записав уравнение второго правила Кирхгофа для цепи на рис.1, получим:

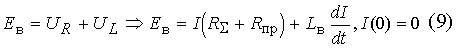
Здесь 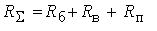- активное сопротивление в цепи, неизменное в течение процесса; 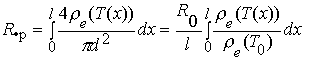сопротивление проволоки с учетом нагрева (R0 - начальное сопротивление проволоки).
Математическая модель. Для численного решения уравнения и граничные условия (7),(9) приводятся к безразмерному виду. Помимо безразмерной величины
сопротивления проволоки Rпр). Все функции от температуры в (7),(9) (теплоемкость, теплопроводность и т.д.) записываются в виде
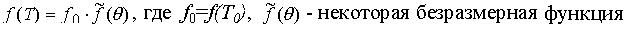
Получаем:

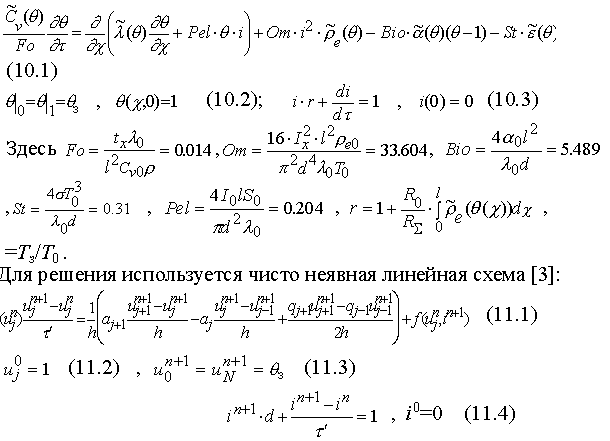
Здесь 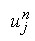- искомая сеточная функция, описывающая распределение температуры, n-индекс временного слоя , j - индекс по координате; - шаг сетки по времени, h - по координате, 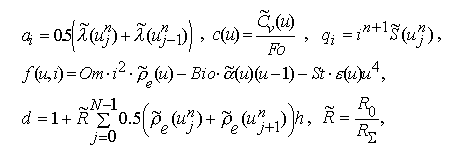N - число шагов по координате (h.N=1). Канонический вид системы (11.1)-(11.3) на n+1 временном слое:
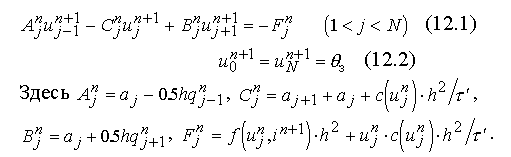На каждом временном слое, начиная с нулевого ( начальное условие ), сначала из (11.4) определяется 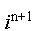затем (12) решается относительно 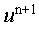методом прогонки [4] .
Все численные расчеты и аппроксимация табличных данных выполнялись при помощи пакета MathCad 2000 Pro.[5].Установлена зависимость коэффициента тепла от температуры

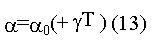
и учитывая зависимость сопротивления от температуры

Уравнение (15) позволяет построить теоретическую вольт- амперную характеристику ЧЭ в среде чистого воздуха.
Перечень ссылок
  1. Исаченко В.П. ,.Осипова В.А., Сукомел А.С "Теплопередача", Москва , Энергоиздат , 1981, С. 207
  2. Протасов Ю.С. , Чувашев С.Н. "Физическая электроника газоразрядных устройств . Эмиссионная электроника" , Москва , Высшая школа , 1992 , С. 181; 205.
  3. Самарский А.А , Гулин А.В. "Численные методы" , Москва , Наука ,1989, С. 281
  4. Амосов А.А , Дубинский Ю.А. , Копченова Н.В. "Вычислительные методы для инженеров" , Москва , Высшая школа , 1994, С 161
  5. Дьяконов В.П. , Абраменкова И.В. "MathCad 2000 в математике, физике и в Internet" , Москва , Нолидж , 2000.

    В библиотеку