
Оптимизация динамических свойств очистных комбайнов нового поколения на стадии их автоматизированного проектирования является актуальной научно-технической проблемой, решение которой позволит увеличить надежность и производительность этих машин. Эта проблема предполагает решение ряда задач научного и практического характера. В их числезадача установления динамических характеристик всех силовых подсистем, прежде всего, тяжелонагруженных подсистем привода исполнительных органов.
Анализ исследований и публикаций: методики эксперимен тального и расчетного определения упругих характеристик подсистем приводов исполнительных органов применительно к очистным ком байнам прежних поколений приведены в ряде работ ученых ДонНТУ, ИГД им. А.А. Скочинского и других организаций [1, 2 и др.]. Безусловно, более высокую точность результатов обеспечивают экспериментальные исследования при наличии натурных образцов машин.Вместе с тем, на стадии автоматизированного проектирования вновь создаваемых очистных комбайнов возможно только расчетное определение рассматриваемых характеристик. Очевидно, что при этом должны учитываться не только крутильные податливости участков валопровода, но и приведенные к крутильным изгибные деформации валов и упругие деформации в опорных узлах корпусов. Поэтому представляет интерес дальнейшее развитие ранее выполненных ра бот, посвященных определению упругих характеристик подсистем приводов исполнительных органов, применительно к новым объектам - очистным комбайнам новых поколений, отличающихся оригинальным структурным построением в виде поворотных блоков резания, наличием торсионных валов и других конструктивных особенностей.
Постановка задачи: задачей настоящей работы является разработка и апробация методики установления упругих характеристик подсистем привода исполнительных органов для очистных комбайнов нового поколения с оригинальными структурными и конструк тивными решениями.
Подсистема ПИО имеет ряд особенностей существенно отличающих ее от подобных подсистем других отечественных очистных комбайнов. Во-первых, это наличие короткой кинематической цепи подсистемы ПИО, реа лизованной в виде поворотного блока резания с завершающим силовым элементом - многопоточной планетарной передачей. Во-вторых, многие силовые элементы валопровода, имеют длину соизмеримую с их диаметром, что затрудняет получение достаточно точных значений их податливостей. В-третьих, деформации корпусных элементов поворотного блока резания не могут быть определены расчетным путем, из-за весьма сложных пространственной конфигурации и силовой картины нагружения. Для некоторых силовых элементов трансмиссии, например, внешнего центрального колеса с окнами для увеличения его податливости отсутствуют зависимости, позволяющие определить их деформации. Нахождение упругих характеристик подсистемы ПИО производилось в два этапа. На первом этапе приведенные к крутильным упругие характеристики силовых элементов валопровода подсисте мы ПИО и их сопряжений определялись расчетным путем (учитывались крутильные, изгибные и контактные деформации). На базе структурного анализа валопровода была составлена следующая структурная формула:

где ешл, ев, езп, е' пл ; е*пл - соответственно податливости шлицевого, гладкого участков вала, зубчатой передачи (приведенная к валу ведомого колеса) и элементов планетарного механизма.
Деформация шлицевого соединения определяется податливостью v: vконтактирующих поверхностей слоев, подвергающихся смятию . Принимая приближенно пропорциональность нормальных давлений и вызываемых ими деформаций смятия, крутильная податливость шлицевого соединения определяется по формуле :

где Кшл- коэффициент шлицевого
соединения;
dшл-средний диаметр шлицевого соединения;
lшл-длина шлицевого соединения ;
hшл-активная высота шлицевого соединения;
Zшл-количество
шлицев, шт.;
Податливость участка круглого вала определяется:
где G-модуль упругости
второго рода, Па;
lв - длина участка вала;
Dв- внешний диаметр участка вала, м;
dв- внутренний диаметр участка вала, м.
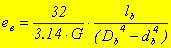
Так как крутящий момент распределяется по длине контакта в шлицевом соединении вал-втулка неравномерно, то расчетную длину вала необходимо принимать равной расстоянию между точками приложения равнодействующих эпюр крутящих моментов на длине контакта шлицев обычно для шлицевого соединения принимается равным 0.333 от длины шлицевого соединения.
Податливость зубчатой передачи определяется изгибными и контактными деформациями зубьев, изгибом валов, на которых установлены зубчатые колеса и упругими деформациями подшипниковых опор.
Определение приведенной к крутильной податливости зубчатой передачи обусловленной изгибом валов и деформациями опор качения выполняется в соответствии с методом Е.И. Ривина . Для этого необходимо определить усилия, действующие на валы, от зубчатых передач и в подшипниковых опорах. Далее определяются податливости подшипниковых опор и координаты векторов перемещений зубчатых колес. Усилия, возникающие в зубчатых передачах, и их направления показаны на рис.2.

Рисунок 2. Усилия действующие в зубчатых зацеплениях.
Податливость планетарной передачи определялась предложенной нижеметодике при этом, принимались во внимание следующие допущения:
Обычно блок сателлитов или ряд содержит три сателлита для компенсации радиальных усилий в зубчатом зацеплении. С целью упрощения анализа механизм приводится к условному, содержащему по одному сателлиту в блоке.
Для определения податливости планетарной передачи (eпл)рассмотрим систему нагрузок, действующих на ее элементы (рис.3).

Рисунок 3. - Система нагрузок планетарной передачи.
Податливости элементов планетарной передачи, определя лись по известным зависимостям. Дляопределение податливость ет, соответствующей двум участкам внепшего центрального колеса (конструкция представлена на рис.4) - зубчатому венцу и перемычки между зубчатыми венцами с окнами для увеличения податливости этого участка, была создана программа, на основе применения метода конечных элементов.

Рисунок 4. Конструкция внешнего солнечного колеса.
Эта программа позволяет решать плоские задачи нагружения системы конечных элементов узловыми усилиями. В качестве базового элемента в ней используется наиболее простой треугольный элемент. С помощью этой программы были найдены ориентировочные значения деформаций одной из пятнадцати эквивалентных (реальная конструкция заменялась плоской) перемычек (см. рис.5), на основе которых била получена величина податливости

Рисунок. 5. Реальная и эквивалентная перемычки и нагрузки действующие на них.
Более точное решение этой задачи было найдено в специализированном пакете программ позволяющем рассматривать большее количество конечных элементов и получать визуализацию результатов. Недеформирован- ная (используемая при решении задачи) и деформированная (результат решения) сетки конечных элементов приведены на рис.6.

Рисунок 6. Недеформированная и деформированная сетки конечных элементов для эквивалентной перемычки.
Таким
образом были определены абсолютные значения податливостей
участков валопровода
между сосредоточенными массами, значения которых соответственно составили:
Динамическая
значимость той или иной податливости определяется ее
долей в общей
потенциальной энергии подсистеме, таким образом по
абсолютным
значениям податливостей участков находятся их приведенные зна
чения. В качестве центра приведения
принимается, как и в случае с моментами
инерции, ротор электродвигателя. Значения приведенных податливостей
соответственно равны.
Расчетное определение
податливостей, учитывая особенности конструкции, является приближенным, однако
дает возможность определить характер распределения податливости вдоль
валопровода и рациональным образом
спланировать второй этап - экспериментального определения (обосно
вать необходимое количество участков подсистемы,
податливости которых должны быть
определены экспериментально)
Наиболее точное
значение податливости может быть получено в результате соответствующего
экспериментального определения. С этой целью
сотрудниками ДонHТУ совместно с ОАО ГМЗ был подготовлен и
выполнен эксперимент по определению
жесткостных характеристик подсистемы ПИО
очистного комбайна KDK 500. Для выполнения эксперимента на ОАО ГМЗ был
изготовлен ряд приспособлений.Результаты расчетов показаны зависемостью крутящего
момента М от Vр и hр(рис.7)

Рис. 7 - График зависимости момента М(Vp;h)
Как известно, принцип работы любого виброзащитного
устройства, являющегося по сути корректирующим
динамическим звеном (КДЗ) для подсистем привода
исполнительных органов выемочных комбайнов, состоит в поглощении и рассеивании
энергии механических колебаний, что обеспечивает снижение коэффициента
вариации крутящего момента по всей длине упругого валопровода
редуктора. При этом рассеиваемая энергия в виде потерь на трение в КДЗ трансn
формируется в тепловую энергию, проявляющуюся в
нагреве как элементов самого КДЗ, так и непосредственно сопряженных с ним
деталей или узлов подсистемы привода исполнительных органов.
В настоящей работе разработана методика установления температуры
нагрева исполнительных органов выемочных
комбайнов, в которые встроены корректирующие
динамические звенья.
Уравнение теплового баланса
исполнительного органа с КДЗ при его длительной
работе с постоянной нагрузкой можно в первом приближении записать в сле
дующем виде:
Wdt =Gadr+Fyrdt
где:Wdt-количество тепла,
выделяющегося в исполнительном органе с КДЗ за
время dt,
Дж;
W—мощность потерь на
трение в КДЗ, Вт;
Gadt- количество тепла,
необходимое для повышения температуры исполнительного органа с КДЗ на величину
, Дж;
Ga- теплоемкость исполнительного органа с КДЗ, характеризующая
количество тепла, необходимого для повышение на 1° С температуры исполнительного
органа, имеющего массу G и удельную теплоемкость а, Дж/град;
Fyrdt-количество тепла, отводимое во внешнюю среду
за время dt,Дж;
Fy- теплоотдача
исполнительного органа с КДЗ, характеризующая количе
ство тепла, выделяемого исполнительным
органом с площадью поверхности
F и коэффициентом теплоотдачи в окружающую среду в единицу
времени при разности их температур 1° С,
Дж/страд.
При составлении
уравнения теплового баланса приняты следующие допуще
ния:
1.Исполнительный орган с КДЗ представляет собой
однородное тело,имею
щее одинаковые тепловые свойства всей массы, не изменяющиеся во времени.
2.Теплоемкость окружающей среды равна бесконечности.
3.Мощность потерь на трение является величиной постоянной.
Фактический
тепловой баланс исполнительного органа с КДЗ можно в первом приближении
рассмотреть, приняв допущение, что установившийся режим рабо
ты исполнительного органа в составе выемочного
комбайна является, как и для приводного электродвигателя,
повторно-кратковременным. При этом предполагается
, что при установившемся режиме работы средний уровень
крутящего момента в редукторной группе
подсистемы привода исполнительного органа
средняя мощность потерь на трение
в КДЗ
W время работы исполнительного органа время паузы в течение достаточно
продолжительного периода являются величинами постоянными. Тогда конечная
т к и начальная т н
температуры перегрева
исполнительного органа с КДЗ фиксируемые
соответственно в конце и начале его работы.
Таким образом,
разработанная методика позволяет определять величину как
средней, так и конечной (более высокой)
температуры перегрева исполнительных органов выемочных комбайнов со встроенными
корректирующими динамическими звеньями и с
учетом реальной температуры внешней среды оценивать их температуру нагрева при
работе с различными уровнями средней нагрузки. Эти результаты необходимы для
принятия решения о необходимости проектирования принудительной системы
охлаждения исполнительных органов, а также для выбора параметров данной
системы, если ее необходимость доказана.