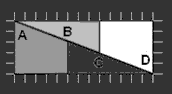
Рисунок 1
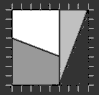
Рисунок 2
Донецкий национальный технический университет, ул. Артема 58, Донецк, 83000,
тел.8(0622)99-99-01, E-mail:info@donntu.ru
| "О сколько нам открытий чудных
готовит просвещенья дух: и гений, парадоксов друг, и опыт, сын ошибок трудных." А.С.Пушкин |
Процесс познания человеком окружающего мира можно сравнить с радостным торжеством, ибо каждая раскрытая тайна укрепляет веру в свои силы. Но на пути победоносной человеческой мысли возникают большие, казалось бы непреодолимые, преграды, перед которыми были бессильными умозаключения. Древнегреческий философ Диодор Кронос (примерно307 год до н.э) не решив одну из древнейших логических задач - парадокс Эвклида, умер от разочарования, а другой философ Фигет Косский, познав такую же неудачу, покончил жизнь самоубийством. Древнегреческие ученые сталкивались с такими задачами в математике. Они прикладывали много усилий, чтобы выявить механизм образования таких загадок. Было установлено, что наши рассуждения тоже подчинены определенным законам (законам логики), нарушение которых обесценивает результаты, добытые в этих рассуждениях. Неразрешенность задач, с которыми встретились Диодор Кронос и Фигет Косский, объясняется как правило, нарушением законов логики. Поэтому уже тогда остро встал вопрос о системе "профилактических приемов" -определенных правил с целью устранения логических ошибок. Первая в истории проба проведения "логической профилактики" в математике принадлежит гениальному древнегреческому математику, автору "Начал" - Эвклиду (IV в до н.э.)Он создал удивительный сборник "Псевдарий", где помещая разнообразные ошибочные рассуждения, к которым часто приходят те, кто начинает играть в математику. Таким образом, Эвклид был автором первого из известных сборников математических софизмов и парадоксов. Остается сожалеть, что этот труд не дошел до нас. Зато требовательность Эвклида и строгость к культуре рассуждений нашла многочисленных последователей. Они собрали и опубликовали большую коллекцию математических софизмов и парадоксов. В наше время ученые продолжают это дело совсем не для того, чтобы удивить кого-то. Человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искустнейше замаскирована ошибка, тем больше удовлетворения приносит он тому кто разгадал его, так как это - маленькое открытие и прекрасная школа, культура математических вычислений. Сборники математических софизмов и парадоксов были всегда популярными. Так в 1846 году М.Г.Чернышевский писал брату Александру:"... сижу 11 недель и 3 дня и никак не разгрызу орешек. Нe поможешь ли мне? Я дал слово не вставать со стула, пока не решу эту задачу. Но что-то не удаётся; помоги хоть ты, лишь на тебя надежда. Вот она. Квадрат любой стороны в любом треугольнике равен сумме квадратов двух других сторон." М.Г.Чернышевский поместил в письме рисунок и доказательства, которые привели к интересному софизму (этот софизм приведен далее).
Этот доклад не просто предлагает задачи из занимательной математики, но и приглашает в своеобразное путешествие неспокойными дорожками человеческой мысли.
| "Людям, которые желают идти
верной дорогой, важно также знать и об отклонениях." Аристотель |
Что такое истина?
В философском понятии истина есть вполне определенное отображение человеком реальной действительности предмета познания таким, каким он есть независимо от нашего сознания и вне его. Истина занимает особое место в жизни человека. Она приносит радость и огорчение, увлекает и вызывает злость, парализует волю слабых и ведет на подвиги сильных. Выдающийся древнегреческий философ материалист Демокрит (460-370 лет до н.э.) говорил, что доказательство теоремы ему дороже чем царственный престол. Великий итальянский ученый Джордано Бруно (1548 - 1600) познал жестокие преследования и пошел на огонь инквизиции ради научной истины. В 1820 году венгерский математик Фархаш Бойян писал своему сыну Яношу, когда узнал, что тот берется за доказательство V постулата Эвклида: "Ты не должен пытаться одолеть теорию параллельных линий: я знаю этот путь, я прошел его до конца, я пережил эту беспросветную ночь и весь свет, всю радость моей жизни я похоронил в нем. Молю тебя забудь учение параллельных оно лишит тебя здоровья, потом оно лишит тебя радости жизни. Это - беспросветная тьма может поглотить тысячами таких талантов, как Ньютон... Я готов был стать мучеником этой истины, чтобы только очистить геометрию от этого пятна. Я проделал страшную, гигантскую работу, я достиг значительно больше, чем то, что было найдено до меня, но полного удовлетворения я не получил!" Предупреждения были напрасными. Янош Бойян прошел весь трудный путь по раскрытию тайны параллельных прямых, познал радостные минуты первооткрывателя и горькие часы и даже годы непризнания его парадоксальных в то время результатов.
Пытливая человеческая мысль проявляла неисчерпаемую находчивость, изворотливость и силу, отвоевывая её тайны. То, что казалось очевидным, часто оказывалось ошибкой. Люди наблюдают, как "Солнце вращается вокруг Земли", в действительности это движение есть зрительное следствие движения Земли вокруг Солнца и своей оси. А сколько неправильной информации поступает от наших органов чувств, когда оцениваются расстояния, размеры тел, отрезки времени, положение предметов в пространстве, их цвет. В " Сфинксе " Эдгар По описывает такой случай с героем рассказа; " Дело в том", что скоро по приезду в коттедж со мной случилось что-то непонятное и зловещее... Я был настолько потрясен, что прошло много дней, прежде чем я отважился рассказать об этом моему товарищу. В конце жаркого дня я сидел с книжкой в руках около открытого окна, откуда открывался вид на берег речки и на отдаленный пригорок, с ближайшего к нам бока - безлесный, вследствие, так называемого оползня. Мысли так давно уже оторвались от книжки и, отведя глаза от страницы, я увидел оголенный склон, а на нем мерзкую тварь, которая быстро спускалась с пригорка и скрылась в густом лесу около его подножья. При появлении этого существа я сначала подумал, что я сошел с ума, но во всяком случае не поверил своим глазам. Прошло немало времени, прежде чем я убедился, что не сплю и не сошел с ума. Но если я опишу тварь, которую я четко увидел и имел возможность наблюдать, пока она спускалась по склону, читателям ещё труднее чем мне будет в неё поверить. "Страшной тварью оказалась... кошка , которая проползла по паутине вдоль оконной рамы. Сопоставления и гиперболизация воображаемых образов заставили героя рассказа пережить минуты глубокого потрясения.
Чтобы избежать подобных ситуаций человек с первых шагов своей деятельности прибегает к другому методу познания мира, который помогал не только критиковать, но и корректировать познания через органы чувств. Этим методом стало мышление. Только благодаря мышлению удаётся объяснить и уточнить факты, выявленные в результате наблюдений и опытов. Высшей формой умственной деятельности человека есть теоретическое мышление. Среди различных теоретических методов познания мира наиболее мощным стал математический метод. Он занял особое место в познании по масштабам применения. Выдающийся 41ранцузский философ и математик Пьер Гассенди (1592 - 1635) писал: "Тот, кто с детства проникся математикой, усвоив её непростые доказательства, так подготовлен к принятию истины, что легко отбросит любую фальшь."
Математика важна для студента не только как основа дальнейшего технического и профессионального обучения. Она важна потому, что учит его точному и правильному мышлению. А мыслить правильно нужно всем: инженеру, ученому, врачу, писателю, артисту.
Софизм 65=64.
 Рисунок 1 |
 Рисунок 2 |
На рисунке 1 имеем на клетчатой бумаге нарисованный прямоугольник размерами 5 x 13, т.е. площадью 65. На рисунке 2 имеем квадрат 8 x 8 = 64. Обе фигуры разрезаны на попарно равные части. Отсюда, их площади равны; следовательно, 64 = 65.
В этом софизме проявляется еще одно интересное свойство чисел Фибоначчи (он же Леонардо Пизанский (1180 - 1240), итальянский математик). Вкратце это так: первоначальный прямоугольник 5 x 13 разрезан на такие части, что 5 + 8 = 13 (по оси x). Квадрат же составлен 8 x 8, т.е. среднее между числами 5 и 13 в ряде Фибоначчи.
Софизм равенства катета гипотенузе, или все треугольники равносторонние.
Рассмотрим произвольный треугольник ABC(рис.3). Проведем биссектрису угла B и серединный перпендикуляр к стороне AC; точку их пересечения назовем O. Опустим из нее перпендикуляры EO и OF на стороны AB и BC соответственно.
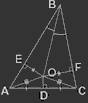
Рисунок 3
Т.к. DO одновременно и высота и медиана треугольника AOC, то он равнобедренный и AO = OC. Т.к. BO - биссектриса, то, из равенства треугольников EBO и OBF (откуда EB = BF), EO = OF. Следовательно, треугольник AEO равен треугольнику FCO, т.е. AE = FC. Отсюда, т.к. AB = AE + EB и BC = BF + FC, AB = BC. Проведя такое же рассуждение для основания не AC, а, например, AB, получим, что BC = CA.
Из этого следует, что все треугольники на свете - равносторонние. В частном случае, если треугольник прямоугольный, то катеты равны гипотенузе.
Софизм, названный мною "парадоксом" равных отрезков, или полуокружность длиннее прямой.
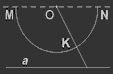 Рисунок 4 |
 Рисунок 5 |
Рассмотрим треугольник ABC(рис.5). Проведем прямую MN параллельно AB так, как показано на рисунке. Теперь для любой точки L стороны AB проведем прямую CL, которая пересечет MN в точке K. Таким образом установим однозначное соответствие между отрезками AB и MN, т.е. они оба содержат одинаковое количество точек. Значит, имеют одинаковую длину.
Аналогичным способом для любой точки K(рис.4) полуокружности MN установим однозначное соответствие с точками прямой a. Но у нас останутся две точки, а именно M и N, для которых это соответствие не установим. Следовательно, в полуокружности на две точки больше, а значит, полуокружность длиннее прямой.