 |
Steve MacDonald, Duane Szafron, and Jonathan Schaeffer
Department of Computing Science, University of Alberta
{stevem,duane,jonathan}@cs.ualberta.ca, http://www.cs.ualberta.ca/~{stevem,duane,jonathan}
Оригинал статьи:http://www.cs.ualberta.ca/~systems/papers/COOTShtml/paper.html
Parallel programming offers potentially substantial performance benefits to computationally intensive applications. Using additional processors can increase the computational power that can be applied to large problems. Unfortunately, it is difficult to use this increased computational power effectively as parallel programming introduces new complexities to normal sequential programming. The programmer must create and coordinate concurrency. Synchronization may be necessary to ensure data is used consistently and to produce correct results. Programs may be nondeterministic, hampering debugging by making it difficult to reproduce error conditions.
We need development tools and programming techniques to reduce this added programming complexity. One such tool is a parallel programming system (PPS). A PPS can deal with complexity in several ways. It can provide a programming model that removes some of the added complexity. It can also provide a complete tool set for developing, debugging, and tuning programs. However, it is likely that there will still be some additional complexity the user must contend with when writing parallel programs, even with a PPS. We can ease this complexity by using new programming techniques, such as design patterns and object-oriented programming. Design patterns can help by documenting working design solutions that can be applied in a variety of contexts. Object-oriented programming has proven successful at reducing the software effort in sequential programming through the use of techniques such as encapsulation and code reuse. We want to apply these benefits to the more complex domain of parallel programming.
The CO2P3S1 parallel programming system supports pattern-based parallel program development through framework generation and multiple layers of abstraction [8]. The system can be used to parallelize existing sequential code or write new, explicitly parallel programs. This system automates the use of a selected set of patterns through pattern templates, an intermediary form between a pattern and a framework. These pattern templates represent a pattern where some of the design alternatives are fixed and others are left as user-specified parameters. Once the template has been fully specified, CO2P3S generates a framework that implements the pattern in the context of the fixed and user-supplied design parameters. Within this framework, we introduce sequential hook methods that the user can implement to insert application-specific functionality. In the CO2P3S programming model, the higher levels of abstraction emphasize correctness and reduce the probability of programmer errors by providing the parallel structure and synchronization in the framework such that they cannot be modified by the user. The lower layers emphasize openness [14], gradually exposing low-level implementation details and introducing more opportunities for performance tuning. The user can work at an appropriate level of abstraction based on what is being tuned.
The key to reducing programmer errors is the decomposition of the generated framework into parallel and sequential portions. The framework implements both the parallel structure of the program and the synchronization for the execution of the hook methods. Neither of these attributes of the program can be modified at the highest level of abstraction. This decomposition allows the hook methods to be implemented as sequential methods, so users can concentrate on implementing applications rather than worrying about the details of the parallelism.
We introduce phased parallel design patterns in this paper. Phased patterns are unique in that they express a temporal relationship between different phases of a parallel program. Although all patterns have temporal aspects (such as specific sequences of method invocations), the intent of phased patterns is to deal with changing concurrency requirements for different phases of a parallel program. We introduce two such patterns, the Method Sequence and the Distributor, both of which are new. The Method Sequence can be used to implement phased algorithms, explicitly differentiating between the different phases of a parallel algorithm. This pattern recognizes that efficiently parallelizing a large program will likely require the application of several parallel design patterns. The Distributor pattern allows the user to selectively parallelize a subset of methods on an object, acknowledging that not all operations may have sufficient granularity for parallel execution.
We also introduce a structural pattern, the Two-Dimensional Mesh. The Mesh was written in an object-oriented fashion to fit within the CO2P3S system.
To demonstrate the use of the CO2P3S system, we present the development of two example programs. Our first example, reaction-diffusion texture generation [17], uses the Mesh pattern to simulate the reaction and diffusion of two chemicals over a two-dimensional surface. The second program implements the parallel sorting by regular sampling algorithm [13] using the Method Sequence and Distributor patterns. Both programs are implemented using the facilities provided at the highest level of abstraction in CO2P3S to demonstrate the utility of our patterns and the utility of the frameworks we generate to support our pattern templates.
The research contributions of this paper are:
This section presents a brief overview of the CO2P3S system. A more detailed description can be found in [8].
The CO2P3S parallel programming system provides three levels of abstraction that can be used in the development of parallel programs. These abstractions provide a programming model that allows the programs to be tuned incrementally, allowing the user to develop parallel programs where performance is more directly commensurate with effort. These abstractions, from highest to lowest, are:
Several critical aspects of the framework are demonstrated by the use of hook methods for introducing application-specific functionality. First, the parallel structural code cannot be modified in the Patterns Layer, which allows us to make correctness guarantees about the parallel structure of the program. Second, it allows users to concentrate on implementing their applications without worrying about the structure of the parallelism. Also, by ensuring that the structural code provides proper synchronization around hook method invocations, the user can write sequential code without having to take into account the parallelism provided by the framework. Lastly, we provide suitable default implementations of the hook methods in the abstract classes of the framework. These default methods permit the framework to be compiled and executed immediately after it is generated, without implementing any of the hook methods. The program will execute with a simple default behaviour. This provides users with a correct implementation of the structure of the pattern before they begin adding the hook methods and tuning the program.
The CO2P3S system currently supports several parallel design patterns through its templates, which also use a group of sequential design patterns. These patterns are written specifically for solving design problems in the parallel programming domain. The patterns used in this paper are:
The context of our patterns is the architecture and programming model of CO2P3S. Therefore, we have made several changes to the structure of the basic design pattern documentation [4]. Since our patterns are for the parallel programming domain, the pattern description includes concurrency-related specifications, such as synchronization and the creation of concurrent activity. From the pattern, we produce a CO2P3S pattern template and an example framework, which we also describe in the pattern document. While these two sections are not strictly pattern specifications, they illustrate the use of the pattern while documenting the CO2P3S templates and frameworks. So while we have added CO2P3S-specific sections to our pattern descriptions, we have preserved the instructional nature of design patterns.
We note that our patterns still represent abstract design solutions. From the abstract pattern, we fix some of the design tradeoffs and allow the user to specify the remaining tradeoffs using parameters. This intermediate form, which is less abstract than a pattern but less concrete than a framework, is called a pattern template. We use a fully specified pattern template to generate parametrically related families of frameworks, with each framework in the family implementing the same basic pattern structure but specialized with the user-supplied parameters. However, the pattern templates are a design construct used to specify a framework; the templates do not contain nor provide code themselves. The generated frameworks provide reusable and extendible code implementing a specific version of the pattern. These frameworks take into account our decomposition of a program into its sequential and parallel aspects. The ability of the user to modify a framework is dictated by the level of abstraction that the user is using.
In creating the pattern templates, we try to fix as few of the design tradeoffs as possible. However, in fixing any part of the design, we will create situations in which it will be necessary to modify certain elements of a program to fit within the limitations we impose. For the example programs that follow, we discuss the design in terms of the patterns, and discuss the implementation in terms of the pattern templates and the frameworks. The implementation of the programs may need to be modified from the initial design to account for the fixed design tradeoffs in the pattern templates and frameworks.
In this section, we detail the design and implementation of two example programs. These examples demonstrate the applicability of our patterns to application design, and show how the pattern templates and generated frameworks can be used to implement the programs. The first example uses a reaction-diffusion texture generation program to show how we have reworked the Mesh pattern in an object-oriented fashion. The second example, parallel sorting by regular sampling, uses the Method Sequence and Distributor patterns. We also use this example to highlight the temporal nature of these two patterns and to show the composition of CO2P3S frameworks. The implementation of these two examples demonstrates that the Patterns Layer of CO2P3S can be used to write parallel programs with good performance. It also shows the benefits of a high-level object-oriented tool for parallel programming.
Reaction-diffusion texture generation [17] can be described as two interacting LaPlace equations that simulate the reaction and diffusion of two chemicals (called morphogens) over a two-dimensional surface. This simulation, started with random concentrations of each morphogen on the surface, can produce texture maps that approximate zebra stripes. The problem uses Gauss-Jacobian iterations (each iteration uses the results from the previous iteration to compute the new values, without any successive overrelaxation) and is solved using straightforward convolution. The simulation typically executes until the total change in morphogen concentration over the surface falls below some threshold. We use a fully toroidal mesh, allowing the morphogens to wrap around the edges of the surface. The toroidal boundary conditions ensure that the resulting texture can be tiled on a display without any noticeable edges between tiles.
An obvious approach to this problem is to decompose the two-dimensional surface into regular rectangular regions and to work on these regions in parallel. Our solution must be more complex because we cannot evaluate each region in isolation. Each point on the surface needs the concentration values from its neighbours to calculate its new value, so points on the edge of a region need data from adjoining regions. Thus, we require an exchange of region boundaries between iterations. Further, Gauss-Jacobian iterations introduces dependencies between iterations that need to be addressed by our parallel implementation of this problem.
The first step in implementing a CO2P3S program is to analyze the problem and select the appropriate design pattern. This process still represents the bottleneck in the design of any program. Given the requirements of our problem, the Mesh pattern is a good choice for several reasons. The problem is an iterative algorithm executed over a two-dimensional surface. Further, our approach is to decompose the surface into regular rectangular regions, a decomposition that is automatically handled by the framework for the Mesh pattern template.
The Mesh pattern consists of two types of objects, a collector object and a group of mesh objects. The structure of the Mesh is given in Figure 1. The collector object is responsible for creating the mesh objects, distributing the input state over the mesh objects, controlling the execution of the mesh objects, and collecting the results of the computation. The mesh objects implement an iterative mesh computation, a loop that exchanges boundaries with neighbouring mesh elements and computes the new values for its local mesh elements. The iterations continue until all the mesh objects have finished computing, when all of the morphogen concentrations in all of the mesh objects have stabilized in our example.
 |
This pattern requires synchronization because of dependencies between iterations. Specifically, we need to ensure that the boundary elements for each mesh element have all been computed before exchanging them, to prevent a neighbour from using incorrect data in its next iteration. We also require synchronization for determining the termination condition, since all of the mesh objects must cooperate to decide if they have finished. This synchronization is necessarily pessimistic to handle the general case. Individual programs using this pattern may remove any unnecessary synchronization.
The Mesh pattern is not specific to the reaction-diffusion example. It can be used to implement other finite element calculations and image processing applications.
Once the pattern has been selected, the user selects the corresponding pattern template and fills in its parameters. For all pattern templates, the names of both the abstract and concrete classes for each class in the resulting framework are required. In CO2P3S, the user only specifies the concrete class names; the corresponding abstract class names are prepended with ``Abstract''. For our Mesh example, we specify RDCollector for the collector class and RDSimulation for the mesh class, which also creates the abstract classes AbstractRDCollector and AbstractRDSimulation. We further specify the type of the two-dimensional array that will be distributed over the mesh objects, which is MorphogenPair for the reaction-diffusion example. Finally, we specify the boundary conditions of the mesh, which is set to fully toroidal (where each mesh object has all four neighbours by wrapping around the edges of the mesh, as shown in Figure 1). We can select other boundary conditions (horizontal-toroidal, vertical-toroidal, and non-toroidal); we will see the effects of different conditions later in this section. The dimensions of the mesh are specified via constructor arguments to the framework. The input data is automatically block-distributed over the mesh objects, based on the dimensions of the input data and the dimensions of the mesh.
From the pattern template specification, the CO2P3S system generates a framework implementing the specific instance of the Mesh pattern given the pattern template and its parameters. The framework consists of the four classes given above with some additional collaborator classes. The sequence of method calls for the framework is given in Figure 2.
 |
Once the framework is generated, the user can implement hook methods to insert application-specific functionality at key points in the structure of the framework. The selection of hook methods is important since we enforce program correctness at the Patterns Layer by not allowing the user to modify the structural code of the framework. The user implements the hook methods in the concrete class by overriding the default method provided in the abstract superclass in the framework. If the hook method is not needed in the application, the default implementation can be inherited.
To demonstrate the use of the hook methods, we show the main
execution loop of the Mesh
framework, as generated by CO2P3S, in Figure 3. The hook
methods are indicated in bold italics. There are hook methods for both
the collector and mesh objects in the Mesh framework. For the
collector, the only hook method is:
void meshMethod()
|
The implementation of the operate() method called in the code from Figure 3 invokes a subset of the nine operation methods given in Figure 4. The boundary conditions and the position of the mesh object determine which of the operation methods are used. For instance, consider the two meshes in Figure 5. For the fully toroidal mesh in Figure 5(a), there are no boundary conditions. Thus, only the interiorNode() hook method is invoked. For the horizontal-toroidal mesh in Figure 5(b), there are three different cases, one for each row. The mesh objects in the different rows, from top to bottom, invoke the topEdge(), interiorNode(), and bottomEdge() hook methods for the mesh operation. The implementation of the operate() method uses a Strategy pattern [4], where the strategy corresponds to the selected boundary conditions. This strategy is a collaborator class generated with the rest of the framework. It is also responsible for setting the neighbours of the mesh elements after they are created, using the setNeighbours() method (from Figure 2). At the Patterns Layer, the user does not modify this class. Each mesh object automatically executes the correct methods, depending on its location in the mesh.
void topLeftCorner(MorphogenPair[][] right, MorphogenPair[][] down) ;
|
Now we implement the reaction-diffusion texture generation program using the generated Mesh framework. First, we note that we do not need a reduction method, as the result of the computation is the surface computed by each region. Also, we do not require the outerPrefix() or the outerSuffix() methods. The innerPrefix() method is required because we have chosen to keep two copies of each morphogen array, a read copy for getting previous data and a write copy for update during an iteration. This scheme uses additional memory, but obviates the need to copy the array in each iteration. Each iteration must alternate between using the read and write copies, which is accomplished by reversing the references to the arrays in the innerPrefix() method. Given our fully toroidal mesh, we only need to implement the mesh operation in the interiorNode() hook method.
The notDone() method checks the local mesh state for convergence. Each mesh object returns a Boolean flag indicating if it has finished its local computation, and these flags are used to determine if all of the mesh objects have finished. The pattern template fixes the flags as Booleans, which does not allow the global termination conditions given in Section 3.1 to be implemented. Instead, our simulation ends when the change in morphogen concentration in each cell falls below a threshold. Although this restriction forced us to modify this program, it simplifies the pattern template specification and reduces the number of hook methods. This termination behaviour can be modified at the Intermediate Code Layer if a global condition must be implemented.
After completing the specification and implementation of the Mesh framework, the user must implement the code to instantiate the objects and use the framework. The Java code is given in Figure 6, where we use constants for the width and height of the data and the mesh, but these values could be obtained dynamically at run-time from a file or from the user.
public static void main(String[] argv) |
In this section, we evaluate the Patterns Layer of CO2P3S using the reaction-diffusion texture generator. Our basis for evaluation is the amount of code written by the user to implement the parallel program and the run-time performance. These results are based on a Java implementation of the problem.
In the following discussion, we do not include any comments in counts of lines of code. All method invocations and assignments are considered one line, and we count all method signatures (although the method signatures for the hook methods are generated for the user).
The sequential version of the reaction-diffusion program was 568 lines of Java code. The complete parallel version, including the generated framework and collaborating classes, came to 1143 lines. Of that 1143 lines, the user wrote (coincidentally) 568 lines, just under half. However, 516 lines of this code was taken directly from the sequential version. This reused code consisted of the classes implementing the morphogens. This morphogen code had to be modified to use data obtained from the boundary exchange, whereas the sequential version only used local data. This modification required one method to be removed from the sequential version and several methods added, adding a total of 52 lines of code to the application. The only code that could not be reused from the sequential version was the mainline program. In addition, the user was required to implement the hook methods in the Mesh framework. These methods were delegated to the morphogen classes and required only a single line of code each.
We note that this case is almost optimal; the structure of the simulation was parallelized without modifying the computation. Also, the structure of the parallel program is close to the sequential algorithm, which is not always the case. These characteristics allowed almost all of the sequential code to be reused in the parallel version.
This program was executed using a native-threaded Java implementation from SGI (Java Development Environment 3.1.1, using Java 1.1.6). The programs were compiled with optimizations on and executed on an SGI Origin 2000 with 42 195MHz R10000 processors and 10GB of RAM. The Java virtual machine was started with 512MB of heap space. Results were collected for programs executed with the just-in-time (JIT) compiler enabled and then again with the JIT compiler disabled. Disabling the JIT compiler effectively allows us to observe how the frameworks behave on problems with increased granularity. Speedups are based on wall-clock time and are compared against a sequential implementation of the same problem executed using a green threads virtual machine. Note that the timings are only for the mesh computation; neither initialization of the surface nor output is included. The results are given in Table 1.
| |||||||||||||||||||||||||||||||||||
With the JIT enabled, the speedups for the program tail off quickly. As we add more processors, the granularity of the mesh computation loop falls and the synchronization hampers performance. The non-JIT version shows good speedups, scaling to 16 processors, showing the effects of increased granularity.
From this example, we can see that our framework promotes the reuse of sequential code; almost all of the morphogen code from the sequential program was reused in the parallel version. This reuse allowed the parallel version of the problem to be implemented with only a few new lines of code (52 lines). The performance of the resulting parallel application is acceptable with the JIT enabled, although the granularity quickly falls.
Parallel sorting by regular sampling (PSRS) is a parallel sorting algorithm that provides a good speedup over a broad range of parallel architectures [13]. This algorithm is explicitly parallel and has no direct sequential counterpart. Its strength lies in its load balancing strategy, which samples the data to generate pivot elements that evenly distribute the data to processors.
The algorithm consists of four phases, illustrated in
Figure 7. Each phase must finish before the next
phase starts. The phases, executed on p processors, are:
The parallelism in this problem is clearly specified in the algorithm from the previous section. We require a series of phases to be executed, where some of those phases use a set of processors computing in parallel. For the parallel phases, a fixed number of processors execute similar code on different portions of the input data.
An interesting aspect of the PSRS algorithm is that the parallelism changes in different phases. The first and third phases are similar. The second phase is sequential. Finally, the last phase consists of two subphases (identified below), where each subphase has its own concurrency requirements. We need to ensure that this temporal relationship between the patterns can be expressed. In contrast, other parallel programming systems require the user to build a graph that is the union of all the possible execution paths that are used and leave it to the user to ensure they are used correctly. Alternately, the user must use a pipeline solution, where each pipe stage implements a phase (as in Enterprise [10]). However, the real strength of a pipeline lies in algorithms where multiple requests can be concurrently executing different operations in different pipe stages. Further, a pipeline suggests that a stream of data (or objects in an OO pipeline) is being transformed by a sequence of operations. A phased algorithm may transform its inputs or generate other results, depending on the algorithm.
A further temporal aspect of this algorithm is when to use parallelism. Sometimes we would like to use the same group of objects for both parallel and sequential methods. For instance, some methods may not have enough granularity for parallel execution. Sometimes, as in the second phase of PSRS, we may need to execute a sequential operation on data contained in a parallel framework. This kind of control can be accommodated by adding sequential methods in the generated framework. These methods would use the object structure without the concurrency. In implementing these methods, the user must ensure that they will not interfere with the execution of any concurrent method invocations.
The Method Sequence pattern is a specialization of the Facade pattern [4] that adds ordering to the methods of the Facade. It consists of two objects, a sequence object and an instance of the Facade pattern [4]. The sequence object holds an ordered list of method names to be invoked on the Facade object. These methods have no arguments or return values. The Facade object supplies a single entry point to the objects that collaborate to execute the different phases. The Facade typically delegates its methods to the correct collaborating object, where these methods implement the different phases for the sequence object. Each phase is executed only after the previous phase has finished. The Facade object is also responsible for keeping any partial results generated by one phase and used in another (such as the pivots generated in the second phase of PSRS and used in the third phase). We include the Facade object for the general case of the Method Sequence pattern, where there may be different collaborating objects implementing different phases of the computation. Without the Facade object, the sequence object would need to manage both the method list and the objects to which the methods are delegated, making the object more complicated.
The Method Sequence pattern has other uses beyond this example. For example, it is applicable to programs that can be written as a series of phases, such as LU factorization (a reduction phase and a back substitution phase).
After designing this part of the program, the user selects the Method Sequence pattern template and fills in the parameters to instantiate the template. For this pattern template, the user specifies the names of the concrete classes for the sequence and Facade classes, and an ordered list of methods to be invoked on the Facade object. Again, the abstract superclasses for both classes have ``Abstract'' prepended to the concrete class names.
Now we address the parallelism in the first, third, and last phases. Each of these phases require a fixed amount of concurrency (p processors). If we attempt to vary the number of processors for different phases, we will generate different data distributions that will cause problems for the operations. Further, the processors operate on the same region of data in the first and third phases. If we can distribute the data once to a fixed set of processors, we can avoid redistribution costs and preserve locality. The last phase requires a redistribution of data, but again it must use the same number of processors as used in the previous parallel phases. Similarly, the two subphases for the last phase share a common region, the temporary buffer. It is also necessary for the concurrency to be finished at the end of each phase because of the dependencies between the phases.
Given these requirements, we apply the Distributor pattern. This pattern provides a parent object that internally uses a fixed number of child objects over which data may be distributed. In the PSRS example, the number of children corresponds to the number of processors p. All method invocations are targeted on the parent object, which controls the parallelism. In this pattern, the user specifies a set of methods that can be invoked on all of the children in parallel. The parent creates the concurrency for these methods and controls it, waiting for the threads to finish and returning the results (an array of results, one element per child).
The Distributor pattern can also be used in other programs. It was used three times in the PSRS algorithm, and can be applied to any data-parallel problem.
After the design stage, the user selects the Distributor pattern
template and instantiates the template. For the Distributor pattern
template, the user specifies the names of the concrete classes for the
parent and child classes (again, the abstract classes are
automatically named) and a list
with the following fields:
Based on the specification of the pattern templates for this program, the structure of the framework for the PSRS program is given in Figure 8. The two uses of the Method Sequence framework are the Sorter Sequence and Sorter Facade class pair, and the Merger Sequence and Merger Facade pair. The two uses of the Distributor framework are the Data Container and Data Child pair, and the Merger Container and Merger Child pair. When generated, the framework does not contain the necessary references for composing the different frameworks; creating these references is covered in Section 3.2.5. However, any references needed in a particular framework are supplied in the generated code. For instance, the abstract sequence class has a reference to the Facade object in the Method Sequence framework. The actual object is supplied by the user to the constructor for the sequence class.
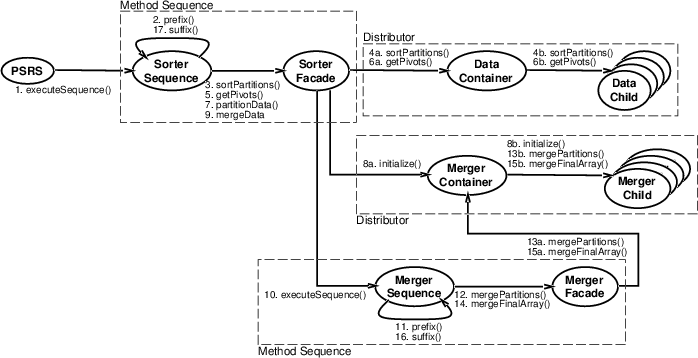 |
Both the Method Sequence and the Distributor frameworks have different hook methods that can be implemented. The sequence of method calls is shown in Figure 8. For the sequence object in the Method Sequence framework, these hook methods are:
For the Distributor framework, the hook methods are the child implementations of the methods specified in the last pattern template parameter. Each child operates independently, without reference to other child objects. These methods can operate on any state that has been distributed across the child objects or can be used to invoke methods on any distributed arguments in parallel. The parent object provides the structural code for this pattern, and has no hook methods. To assist the user, the signatures for the child methods are automatically generated and included in the concrete child class.
Since PSRS is a parallel algorithm, there is no sequential version. Therefore, we chose a sequential quicksort algorithm as a baseline for comparison. The sequential sorting program was 102 lines of Java code, used to initialize the data and verify the sort. The sorting algorithm was the quicksort method from the JGL library [9], which is 255 lines of Java code. The PSRS program, including the framework and collaborator classes, totaled 1252 lines of code (not including the JGL sorting code), 700 of which are user code. 414 lines of the user code are in the three classes Data Child, Merger Child, and Data Container. These classes contain most of the code for the application (the Data Container object is the single processor used for the second phase). Of the remaining classes, the two Facade classes and mainline are the largest. However, the methods in these classes consist mainly of accessors and, particularly in the two Facade objects, one line methods for delegating a method. The mainline also interprets command line arguments, and creates the Sorter Sequence object and the container for the data to be sorted.
In contrast to the reaction-diffusion example, the PSRS algorithm cannot make much use of the code from the sequential version. The problem is that the best parallel algorithm is not necessarily a parallel version of the best sequential algorithm. For instance, the performance of parallel quicksort peaks at a speedup of 5 to 6 regardless of the number of processes [13]. In these cases, writing the parallel algorithm requires more effort, as we see with this problem. Nevertheless, the framework supplies about half of the code automatically, including the error-prone concurrency and synchronization code.
The performance results for PSRS, collected using the same environment given in Section 3.1.3, are shown in Table 2. These timings are only for sorting the data. Data initialization and sort verification are not included.
| |||||||||||||||||||||||||||||||||||
Unlike the reaction-diffusion example, both JIT and non-JIT versions of the PSRS program show good speedups, scaling to 16 processors. The principle reason for this improvement is that there are fewer synchronization points in PSRS; five for the entire program versus two per iteration of the mesh loop. In addition, the PSRS algorithm does more work between synchronization points, even with the smaller data set, reducing the overall cost of synchronization further.
From this example, we can see that CO2P3S also supports the development of explicitly parallel algorithms. The principle difficulty in implementing this kind of parallel algorithm is that little sequential code can be used in the parallel program, forcing the user to write more code (as we can see by the amount of user code needed for PSRS). Support for explicitly parallel algorithm development is crucial because a good parallel algorithm is not always derived from the best sequential algorithm.
Unlike the reaction-diffusion program, the PSRS example used multiple design pattern templates in its implementation, and required the resulting frameworks to be composed into a larger program. We explain briefly how this composition is accomplished, which also provides insights on how the user can augment the generated framework at the Patterns Layer.
In CO2P3S frameworks, composition is treated as it is in normal object-oriented programs, by delegating methods to collaborating objects. Note that the framework implementing a design pattern is still a group of objects providing an interface to achieve some task. For instance, in the code in Figure 6, the collector object provides an interface for the user to start the mesh computation and get the results, but the creation and control of the parallelism is hidden in the collector. If another framework has a reference to a collector object, it can use the Mesh framework as it would any other collaborating object, providing framework composition in a way compatible with object-oriented programming.
To compose frameworks in this fashion, the frameworks must be able to obtain references to other collaborating frameworks. This can be done in three ways: passing the references as arguments to a method (normal or hook) and caching the reference, instantiating the collaborating framework in the framework that requires it (in a method or constructor), or augmenting constructors with new arguments. The first two ways are fairly straightforward. The second method of obtaining a reference is used in the third phase of PSRS since the Merger Container object cannot be created until the pivots have been obtained from the second phase.
The third method of obtaining a reference, augmenting the constructor for a framework, requires more discussion as it is not always possible. We should first note that this option is open to users because the CO2P3S system requires the user to create some or all of the objects that make up a given framework (as shown in Figure 6). In general, users can augment the constructors of any objects they are responsible for creating. For the Mesh framework, the user can augment the constructor for the collector object. However, the added state can only be used to influence the parallel execution of a framework at the Patterns Layer if the class with the augmented constructor also has hook methods the user can implement. Otherwise, the user has no entry point to the structural code and the additional state cannot be used in the parallel portion of that framework. For instance, the user can augment the constructor for the parent object in a Distributor framework, but since the parent has no hook methods this state cannot influence the parallel behaviour of that object. However, new state can always be used in any additional sequential methods implemented in the framework.
We examine work related to the pattern, pattern template, and framework aspects of the CO2P3S system.
There are too many concurrent design patterns to list them all. Two notable sources of these patterns are the ACE framework [11] and the concurrent design pattern book by Lea [6]. This work provides more patterns and attempts to provide a development system for pattern-based parallel programming. Specifically, our pattern templates and generated frameworks automate the use of a set of supported patterns.
There are many graphical parallel programming systems, such as Enterprise [10,14], DPnDP [15,14], Mentat [5], and HeNCE [2]. Enterprise provides a fixed set of templates (called assets) for the user, but requires the user to write code to correctly implement the chosen template, without checking for compliance. Further, applications are written in C, not an object-oriented language. Mentat and HeNCE do not use pattern templates, but rather depict programs visually as directed graphs, compromising correctness. DPnDP is similar to Mentat except that nodes in the graph may contain instances of design patterns communicating using explicit message passing. In addition, the system provides a method for adding new templates to the tool.
P3L [1] provides a language solution to pattern-based programming, providing a set of design patterns that can be composed to create larger programs. Communication is explicit and type-checked at compile-time. However, new languages impose a steep learning curve on new users. Also, the language is not object-oriented.
Sefika et al. [12] have proposed a model for verifying that a program adheres to a specified design pattern based on a combination of static and dynamic program information. They also suggest the use of run-time assertions to ensure compliance. In contrast, we ensure adherence by generating the code for a pattern. We do not include assertions because we allow users to modify the generated frameworks at lower levels of abstraction. These modifications can be made to increase performance or to introduce a variation of a pattern template that is not available at the Patterns Layer.
In addition to verifying programs, Sefika et al. also suggest generating code for a pattern. Budinsky et al. [3] have implemented a Web-based system for generating code implementing the patterns from Gamma et al. [4]. The user downloads the code and modifies it for its intended application. Our system generates code that allows the user the opportunity to introduce application-specific functionality without allowing the structure of the framework to be modified until the performance-tuning stage of development. This allows us to enforce the parallel constraints of the selected pattern template.
Each of the PPSs mentioned above differ with respect to openness. Enterprise, Mentat, HeNCE, and P3L fail to provide low-level performance tuning. However, Enterprise provides a complete set of development and debugging tools in its environment. DPnDP provides performance tuning capabilities by allowing the programmer to use the low-level libraries used in its implementation. Instead, we provide multiple abstractions for performance tuning, providing the low-level libraries only at the lowest level of abstraction.
This paper presented some of the parallel design patterns and associated frameworks supported by the CO2P3S parallel programming system. We demonstrated the utility of these patterns and frameworks at the first layer of the CO2P3S programming model by showing how two applications, reaction-diffusion texture generation and parallel sorting by regular sampling, can be implemented. Further, we have shown that our frameworks can provide performance benefits.
We also introduced the concept of phased design patterns to express temporal relationships in parallel programs. These relationships may determine when to use parallelism and how that parallelism, if used, should be implemented. These phased patterns recognize that not every operation on an object has sufficient granularity to be run in parallel, and that a single parallel design pattern is often insufficient to efficiently parallelize an entire application. Instead, the parallel requirements of an application change as the application progresses. Phased patterns provide a mechanism for expressing this change.
Currently, we are prototyping the CO2P3S system in Java. We are also looking for other parallel design patterns that can be included in the system, such as divide-and-conquer and tree searching patterns. Once the programming system is complete, we will investigate allowing users to add support for their own parallel design patterns by including new pattern templates and frameworks in CO2P3S (as can be done in DPnDP [15]), creating a tool set to assist with debugging and tuning programs (such as the Enterprise environment [10]), and conducting usability studies [14,16].
This research was supported by grants from the National Science and Engineering Research Council of Canada. We are indebted to Doug Lea for numerous comments and suggestions that significantly improved this paper.
Steve MacDonald, Duane Szafron, and Jonathan Schaeffer
Department of Computing Science, University of Alberta
{stevem,duane,jonathan}@cs.ualberta.ca, http://www.cs.ualberta.ca/~{stevem,duane,jonathan}
Оригинал статьи:http://www.cs.ualberta.ca/~systems/papers/COOTShtml/paper.html