| 1) А 2) А \ В |
3) А 4) А |
5) А 6) А |
Наряду с традиционными методами обучения и контроля знаний тестирование быстро становится необходимой частью учебного процесса. Это методическое направление в педагогике вновь возрождается в нашей стране.
Цель проведения экзаменов и другого контроля знаний в тестовой форме состоит в том, чтобы повысить объективность оценки уровня знаний. Когда тестирование знаний в группе студентов проводится по пройденному курсу, то полнота его изучения выявляется как для всей группы в целом, так и индивидуально для каждого студента.
В отличие от традиционного контроля в форме опроса, устного экзамена или зачета, которое отнимает много времени, тестирование проводится для студентов всей группы одновременно и, хотя процесс тестирования в целом менее продолжителен, он дает более объективную картину уровня знаний студентов. Тестирование, независимо от того, проводится оно в письменной форме или посредством компьютеров, психологически меньше нагружает студентов и преподавателей. Результаты тестирования после обработки на компьютере представляются в форме совокупности стандартных статистических показателей, пригодных для установления рейтинга знаний студентов и сравнительных характеристик студенческой группы в целом.
По определению В.С.Аванесова (1998), педагогическим тестом называют систему заданий возрастающей трудности и специфической формы, позволяющей качественно оценить структуру и измерить уровень знаний учащихся.
Чтобы создать корректный педагогический тест по некоторой дисциплине, требуется немало времени и средств. Однако все затраты оправданы выгодами, которые приносит тестирование учебному процессу. Работа по созданию теста проходит поэтапно.
1 этап.. Отбор учебного материала, подлежащего тестовому контролю, и его спецификация. Определяется круг тем, включаемых в тест, и относительное количество заданий, которым должен быть представлен каждый раздел курса. Содержание программного материала дисциплины разбивается на 5-6 смысловых блоков, примерно определяется содержательный вес каждого модуля так, чтобы процентное соотношение вопросов, формируемых по каждому блоку, соответствовало весу модуля.
2 этап. Создание заданий в тестовой форме по всему курсу или по проверяемой его части, объединение их в тематические группы, комплектование первичного, пробного, теста.
3 этап. Проверка первичного теста на группе испытуемых (студентов)
4 этап.. Статистический анализ результатов первичного тестирования, выбраковка и корректировка тестовых заданий.
5 этап. Формирование из прошедших проверку заданий собственно теста, который должен состоять из заданий в тестовой форме возрастающей трудности с учетом необходимого уровня усвоения знаний и максимально охватывающих всю программу дисциплины.
6 этап. Эмпирическая проверка теста для уточнения педагогических характеристик как отдельных тестовых заданий, так и всего теста в целом, его валидности, надежности и др.
Задания, входящие в тест, подбираются так, чтобы они давали основу для проверки некоторых из таких категорий приобретенных знаний, как названия, имена; формулы; смысл слов, названий и имен; факты; определения; сравнение, сопоставление объектов; противоположности, противоречия, антонимы и т.п.; ассоциации; классификации; причинно-следственные отношения; алгоритмы, процедуры; технологии и технологические понятия; вероятностные понятия; абстрактные понятия; методология предмета (Аванесов, 1998)
Хорошо составленный тест обеспечивает широту охвата содержания предмета и проверяет глубину знаний, полученных студентами.
С развитием технологической (прежде всего компьютерной) базы обучения тестирование становится средством не только обучения, но и самообучения. Интернет способствует быстрому развитию самой идеи образования, расширив и качественно изменив возможности доступа к информации, приведя к созданию дистанционного образования.
В этих условиях хорошо составленные тесты по разным областям знания становятся необходимой частью любого учебного процесса. Однако методической литературы для преподавателей по тестологии пока недостаточно.
Форма задания, в соответствии с методическими задачами, может относиться к одной из четырех основных категорий. Рекомендуется использовать задания с выбором одного или нескольких правильных ответов, задания открытой формы, задания на установление соответствия, а также задания на установление правильной последовательности (Аванесов, 1998)
Короткие инструкции, общие для всех испытуемых, обычно помещаются перед заданием или группой заданий и по шрифтовому оформлению отличаться от содержательной основы задания и ответов к нему. Инструкции адекватны форме и содержанию задания. Если задания представлены одной формой, инструкция пишется один раз для всего теста. Если же тест включает в себя задания различных форм, то перед каждой сменой формы задания пишется новая инструкция.
Задание формулируется в утвердительной, а не в вопросительной форме. Содержательную часть задания не перегружают второстепенными деталями; она включает минимум ключевых слов, необходимых для правильного понимания задания, потому что формулировки заданий должны иметь однозначное толкование.
Немаловажное значение имеет шрифтовое оформление задания. Оно должно быть таким, чтобы суть задания понималась с одного взгляда. Традиционно текст задания пишется прописными буквами, а варианты ответов – строчными.
Правила оценки выполнения каждого задания разрабатываются вместе с тестом, они всегда одинаковы для всех испытуемых. Чаще всего, за верный ответ принято давать один балл, за неверный – ноль. В таком случае сумма всех баллов, полученных студентом, равна числу его правильных ответов. Однако можно использовать и другие шкалы оценок. Сумма баллов ассоциируется с уровнем знаний студента. Совокупность сумм баллов испытуемых используется для установления их рейтингов, то есть порядковых номеров, показывающих сравнительную оценку достижений в рамках данной группы.
Опишем четыре формы заданий, применяемых для формирования теста. Тестовые задания, приводимые здесь в качестве примеров и иллюстраций, сконструированы на основе математических и экономических учебных курсов. Авторы заданий - сотрудники кафедры прикладной математики и информационных технологий Дальневосточного государственного университета проф. Л.Т.Ащепков, преподаватели А.А.Величко и Д.В.Давыдов, а также ст. науч. сотр. Рег. центра качества при ДВГУ Л.Я Ащепкова.
Это простейший вид задания, в котором правильный ответ уже содержится, и задача испытуемого состоит в его узнавании.
Рассмотрим основные элементы заданий с выбором правильного ответа. К ним относятся инструкции для испытуемых, содержание заданий, форма, содержание и число ответов, а также оценки за правильность выполнения.
ИнструкцииВ заданиях с выбором ответа применяют один из двух вариантов инструкций,
соответствующих двум вариантам заданий. Инструкция помещается перед заданием,
она печатается шрифтом, отличающимся от шрифта самого задания, например, более
жирным:
ОБВЕДИТЕ КРУЖКОМ НОМЕР ПРАВИЛЬНОГО ОТВЕТА:
или
ОБВЕДИТЕ КРУЖКОМ НОМЕРА ВСЕХ ПРАВИЛЬНЫХ ОТВЕТОВ:
Задание представляет собой часть утвердительного предложения, но не вопрос. Предлагаемые варианты ответов дополняют его до полного утвердительного предложения. Задача испытуемого – выбрать правильный вариант утверждения, используя знания, полученные в ходе изучения дисциплины. Содержательная основа задания должна быть такой, чтобы для выбора правильного ответа достаточно было вспомнить и применить лишь то, что звучало на лекциях и было написано в рекомендованных для изучения пособиях. В конце содержательной части задания нет знаков препинания.
Текст задания обычно пишется прописными буквами, ответы – строчными. Номера заданий следуют в порядке возрастания, после номера ставится точка. Для нумерации ответов используются числа (или строчные буквы) со скобками.
Примеры:Ответы должны быть содержательными и, по возможности, короткими. В конце ответов нет знаков препинания. Места для правильных ответов в разных заданиях выбираются случайным образом. Располагать ответы можно в одну, две и три колонки.
Пример:| 1) А 2) А \ В |
3) А 4) А |
5) А 6) А |
Минимум средств (слов, символов, рисунков и графиков) должен обеспечивать максимальную ясность смысла задания. При подготовке ответов избегают повторов слов, применения малопонятных, редко употребляемых слов, а также неизвестных студентам символов, иностранных слов, затрудняющих восприятие смысла.
Пример:
|
 |
Для объективной оценки знаний студентов им предлагаются так называемые ответы-дистракторы (от англ. to distract - отвлекать). Дистракторы оказывают большое влияние на качество теста. В хорошо составленном задании правильные и неправильные ответы испытуемыми, плохо знакомыми с предметом, выбираются с равной вероятностью.
Примеры:| 1) А – элемент В 2) А – подмножество В |
3) В – элемент А 4) В – подмножество А |
| 1) разделенными 2) приведенными |
3) разделяющимися 4) разнесенными |
| 1) 2) |
3) 4) |
В заданиях с выбором одного правильного ответа вероятность угадывания при двух вариантах ответов составляет 1/2, при трех - 1/3 и т.д.
Ответы к заданиям могут быть выражены словами, числами, графиками. Они не должны представляться в форме "да" или "нет", "верно" или "неверно".
Примеры неправильно составленных заданий:Правильно составленное задание на эту тему может выглядеть, например, следующим образом:
Существует много и других возможностей построить правильное задание в тестовой форме для проверки знаний о соотношении множеств действительных и иррациональных чисел.
Исключается применение таких вариантов ответа, как “правильного ответа нет”, “все ответы правильные” или “все ответы неправильные”.
Чтобы смысл задания лучше понимался, сильные слова «самый», «наибольший», «наименьший», «наилучший» рекомендуется ставить в самом начале основной части задания.
Пример:| 1) зарплата 2) инвестиции |
3) прибыль 4) потребление |
Рассмотрим применение этих принципов на примерах из математики, экономики и моделирования систем.
Если задание содержит два ответа, то, согласно принципу противоречия, второй ответ образуется из первого простым прибавлением отрицательной частицы “не”, отрицающих предлогов и слов так, что этим ответом отрицается смысл не самого задания, а содержания первого ответа:
Примеры:От противоречивых ответов отличаются ответы, построенные по принципу противоположности.
Примеры: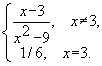 В ТОЧКЕ x=3
В ТОЧКЕ x=3В заданиях с тремя ответами второй ответ может быть противоположен первому, а третий ответ – первому и второму, так что множество ответов полно.
Примеры:Противоположность может быть введена внутрь самих ответов
Пример:| 1) растут 2) падают |
3) сначала растут, потом
падают 4) сначала падают, потом растут |
Принцип однородности состоит в том, что ответы в заданиях должны быть однородными по форме. Не следует использовать в разных ответах одновременно глагол, прилагательное и существительное.
Примеры:| 1) Стьюдента 2) Фишера |
3) Пирсона 4) Бартлета |
Усиливает эффективность заданий, сконструированных по принципу однородности, использование сходных по написанию и звучанию слов, похожих формул.
Примеры: 1) а=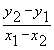 2) а= |
3) b= 4) b= 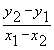 |
| 1) матричной 2) биматричной |
3) двухматричной 4) полиматричной |
| 1) изоквантами 2) изоквантилями |
3) изокостами 4) изопрофитами 5) изоклиналями |
При конструировании ответов можно применить принцип кумуляции признаков, суть которого в том, что каждый следующий ответ содержит на один элемент больше, чем предыдущий:
Примеры:В следующих заданиях одновременно применены принципы противоположности и кумуляции:
Примеры:Применяя принцип сочетания, используют соединение двух, трех или четырех слов в каждом ответе. Можно, например, сочетать более или менее однородные и правдоподобные пары ответов.
Примеры:| 1) прямые линии 2) парабола и прямая |
3) гипербола и прямая 4) гипербола и парабола |
| 1) суммой выигрышей 2) суммой проигрышей |
3) разностью выигрышей 4) разностью проигрышей |
1) равны между собой, но не равны
относительным ценам
2) равны между
собой и равны относительным ценам
3)
не равны между собой, но равны
относительным ценам
4) не равны между
собой и не равны относительным ценам
Ответы сочетаются также по правилу цепочки, причем последнее слово в первом ответе становится первым во втором ответе, последнее во втором – первым в третьем и т.д. Понятия сочетаются по два и по три.
Примеры:Согласно принципу градуирования, ответы в задании упорядочиваются по возрастанию какого-то количественного признака.
Пример:| 1) 9% 2) 10% |
3) 27% 4) 30% |
5) 54% 6) 60% |
| 1) -∞ 2) -1 |
3) 0 4) 1 |
5) 2 6) +∞ |
|
47. ИСХОДЯ ИЗ ПРИВЕДЕННЫХ УСЛОВИЙ УРАВНЕНИЕ КОЛИЧЕСТВЕННОЙ ТЕОРИИ ДЕНЕГ
ПРЕДСКАЗЫВАЕТ ТЕМП ИНФЛЯЦИИ 1) 0,97% 2) 1,53% 3) 2,86% 4) 3,21% |
|
Принцип удвоенного противопоставления применяется в заданиях с четырьмя ответами, части которых, построенные по принципу противоположности, сочетаются попарно.
Примеры:Принцип фасетности содержания задания позволяет использовать фасеты в основном тексте задания. Фасет – это форма записи нескольких вариантов одного и того же задания. Множество слов и словосочетаний, образующих фасет, помещается в столбик и обрамляется фигурными скобками.
Пример:| 1) положительный 2) отрицательный |
3) неположительный 4) неотрицательный |
С помощью фасета создаются параллельные задания. Приведенное выше задание на самом деле содержит краткую запись для четырех параллельных заданий.
Пример одного варианта задания, полученного из задания 38:| 1) положительный 2) отрицательный |
3) неположительный 4) неотрицательный |
Аналогично выглядят три других варианта задания 38 для параметров c2, N, T. Фасет содержания задания может иметь большое количество вариантов. Например, список математических выражений может быть сделан сколь угодно длинным.
Примеры: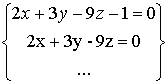 ЧЕРЕЗ НАЧАЛО КООРДИНАТ
ЧЕРЕЗ НАЧАЛО КООРДИНАТКогда в содержательной части задания используется оборот “Если…, то” или эквивалентные ему, то имеет место применение принципа импликации.
Примеры:| 1) 2) |
3) 4) |
| 1) MV = PY 2) MP = VY |
3) M/V = P/Y 4) M/V = P/Y |
При конструировании заданий в тестовой форме, как правило, применяются сочетания принципов, о которых шла речь выше.
Разработчик теста вправе использовать любую обоснованную систему оценки выполнения заданий. Хотя в большинстве случаев за правильно выполненное задание принято давать один балл, а за неправильно выполненное – ноль, однако существуют и другие подходы в оценке. Например, в заданиях с выбором одного правильного ответа можно не ограничиваться дихотомической оценкой и дополнить эту шкалу третьей оценкой, -1, за неправильный ответ, а 0 давать в случае, когда испытуемый не указал никакого ответа. Логика такого подхода состоит в том, что испытуемый, понимающий, что он не может выбрать правильного ответа, потому что по каким-то причинам не усвоил необходимого материала, не заслуживает ни поощрения, ни наказания. Тот же, кто выбрал неправильный ответ, не только очевидным образом показал свое незнание этого вопроса, но, вполне вероятно, выбрал ответ случайно. Такой авантюризм можно наказать отрицательным баллом. Большое количество отрицательных баллов за выполнение отдельных заданий сделает отрицательной сумму баллов испытуемого. Перед тестированием следует предупредить испытуемых, что, если они не знают правильного ответа, то лучше не выбирать никакого или выбрать ответ, специально вводимый для этого случая.
Пример:Впрочем, вычитание балла за любой ошибочный ответ в каждом случае должно быть хорошо педагогически обосновано.
В заданиях с выбором нескольких правильных ответов применимы те же принципы конструирования, что и в заданиях с выбором одного правильного ответа.
Инструкция к таким заданиям имеет вид:
ОБВЕДИТЕ КРУЖКОМ НОМЕРА ВСЕХ
ПРАВИЛЬНЫХ ОТВЕТОВ:
| 1) технологии 2) цен на ресурсы 3) налогов и дотаций 4) числа поставщиков 5) числа покупателей |
6) дохода покупателей 7) ожидания потребителей 8) цен на сопряженные товары 9) объема доступных ресурсов 10) вкусов и предпочтений покупателей |
| 1) y= 2) y=ax+b |
2) y=ax2+bx+c 3) y= |
Если требуется указать не один верный ответ, а несколько из большого числа вариантов ответов, то без знания учебного материала угадать ответ маловероятно, так что информационная ценность заданий этого вида, вообще говоря, выше, чем у заданий с выбором одного правильного ответа.
В заданиях с выбором нескольких правильных ответов используется практически только два принципа композиции – однородность ответов и фасеты в основной части задания.
Задание с выбором нескольких правильных ответов считается выполненным правильно, если точно выбраны все без исключения правильные ответы. Как правило, один балл дается за правильно выполненное задание, ноль – за неправильно выполненное. Можно использовать и более широкую шкалу оценок. Например, за полностью выполненное задание давать 3 балла, за одну ошибку (один лишний ответ или один пропущенный) - 2 балла, и так далее, до нуля. Лишь бы правила оценки были определены заранее и известны испытуемым перед началом тестирования.
Типичные ошибки при разработке заданийНаиболее часто при разработке заданий встречаются логические ошибки, суть которых в несоответствии инструкции содержанию задания, а также основной части задания – ответам. Например, в задании
последний ответ логически противоречит содержанию задания, где утверждается наличие условия.
Следующая типичная ошибка состоит в несоблюдении правила подбора ответов по одному основанию.
Здесь имеют место два основания подбора ответов: одно – выпукла/вогнута, а другое – возрастает/не возрастает.
Типичная ошибка разработчиков тестов состоит в том, что они оставляют в задании избыточную информацию. Более краткие формулировки основной части и ответов могут сделать задание более обозримым без потери его сути. Особенно мешает восприятию задания многословие ответов. Поэтому повторяющиеся слова из ответов рекомендуется выносить в основу задания. Чем короче ответы, тем яснее логика. В следующем примере слово “деятельность” повторяется в обоих ответах.
Пример:Испытуемый, знакомый с предметом, вынужден будет выбрать второй ответ. Однако первообразными данной функции не являются и другие функции, так что есть и другие правильные ответы, которые не были включены в состав этого задания. При дефиците времени задания в форме отрицательных утверждений трудно поддаются логическому анализу.
Типичная ошибка разработчиков тестов заключается и в том, что используется не все пространство возможных комбинаций ответов.
Пример:Используя принцип сочетания, получим более завершенное по строению задание с тремя ответами:
1) f (a)=0 и f '(a)=0Применяя принципы однородности и сочетания, множество ответов можно увеличить до шести элементов:
| 1) f (a)=0 2) f ' (a)=0 3) f '' (a)>0 |
4) f (a)=0 и f' (a)=0 5) f (a)=0 и f'' (a)>0 6) f ' (a)=0 и f'' (a)>0 |
При большом числе возможных ответов рекомендуется использовать задания с выбором нескольких правильных ответов.
Задание открытой формы конструируется в виде утверждения, рядом с которым готовые ответы с выбором не приводятся. Испытуемый сам дописывает в отведенном для этого месте свой ответ так, чтобы в результате получилось истинное высказывание. Эта форма задания сводит возможность догадки к минимуму. С помощью заданий открытой формы проверяют знание названий, формул, имен, фактов, свойств, признаков, дат, причинно-следственных отношений.
Инструкция к заданиям открытой формы может иметь вид:
ДОПОЛНИТЕ:
Если несколько заданий открытой формы следуют одно за другим, то инструкция пишется один раз перед всей группой таких заданий.
Чем ближе к концу фразы находится место для ответа, тем лучше понимается суть задания. В конце задания открытой формы ставится точка.
Примеры:Если в задании открытой формы пропускается два слова, то они могут подбираться по принципу противоположности, как следующем примере.
Пример:При создании заданий открытой формы используются такие принципы композиции, как логическая определенность содержания задания, фасетность, параллельность, обратимость, логическая соразмерность объема определяющего понятия объему определяемого, краткость, неотрицательность и импликация. Рассмотрим на примерах применение этих принципов.
Выполняя задание, построенное в соответствии с принципом логической определенности содержания, испытуемый, знающий содержание предмета, легко находит ответ. Содержание и форма правильно сконструированного задания ведут его мысль прямо к правильному результату.
Пример:Использование принципа фасетности обогащает возможности создания параллельных заданий.
Примеры: ФУНКЦИИ НАЗЫВАЕТСЯ _________.
ФУНКЦИИ НАЗЫВАЕТСЯ _________.
 ,
ТО f(g(x))=___________________.
,
ТО f(g(x))=___________________.
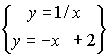 ,
,  и y=0 РАВНА _______________.
и y=0 РАВНА _______________. Чтобы проиллюстрировать применение принципа обратимости, покажем, как одно и то же утверждение может быть преобразовано в несколько заданий открытой формы.
Примеры (из арифметики): ___________.
___________.
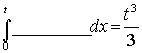
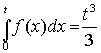 ,
ТО f(x)=____________".
,
ТО f(x)=____________".
 , ТО
a=_____.
, ТО
a=_____. Посредством такого приема создаются параллельные задания для разных вариантов теста.
Кстати, параллельно с последними тремя примерами можно сконструировать, например, задания в рассмотренной выше форме, с выбором правильного ответа.
Пример:
Принцип параллельности предполагает параллельность заданий по содержанию, по форме и по трудности. Параллельность заданий по содержанию обеспечивается применением рассмотренных выше принципов фасетности и обратимости. Использование принципов фасетности и обратимости в заданиях разных форм, имеющих одинаковое содержание, делает эти задания параллельными по содержанию и по форме. Параллельность заданий по содержанию, форме и по трудности имеет место в случаях, когда ко всему выше перечисленному добавляется одинаковая трудность заданий. Обратимся теперь к принципу логической соразмерности объема определяющего понятия объему определяемого.
Нередко оказывается, что задание открытой формы порождает несколько правильных ответов.
Пример:Испытуемый может вписать только “x2”, и его ответ будет таким же верным, как ответы “x2+с", "x2+10” или “x2-1”.
По-видимому, для обеспечения логической соразмерности ответа здесь вместо слова “первообразная” следует использовать “неопределенный интеграл”.
Еще один принцип конструирования заданий в тестовой форме – принцип краткости: чем меньше слов, тем меньше недоразумений:
Примеры: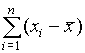 =______.
=______.
Согласно принципу неотрицательности, в основе задания не следует использовать отрицательных частиц или определять понятие, перечисляя элементы, не входящие в него. Приведем здесь пример из книги В.С.Аванесова (1998).
Пример:По определению Евклида, точкой называется то, что не имеет частей. Однако задание, предъявленное в такой форме, студент мог бы дополнить ответом “цвета”, “запаха”, “вкуса”, и был бы логически безупречен, потому что точка действительно не обладает ни одним из этих свойств, как впрочем, и многими другими.
В первой части задания, построенного по принципу импликации, заключено условие, во второй – заключение или вывод.
Посредством заданий открытой формы можно проверять знание терминов.
Пример:Однако, чтобы часто не повторять слово “называется”, вместо него можно ставить тире.
Пример:Несколько последовательных заданий открытого типа, предназначенных для проверки знания терминов, можно объединить в таблицу под условным названием “КАК НАЗЫВАЕТСЯ”. Ответы в этой таблице вписываются испытуемым на специально предназначенные для этого места во втором столбце.
|
ОТВЕТЫ: |
| 1) ПРОЦЕСС ОТЫСКАНИЯ ПРОИЗВОДНОЙ ФУНКЦИИ | _________________ |
| 2) ОПРЕДЕЛЕНИЕ ПРИБЛИЖЕННОГО ЗНАЧЕНИЯ ФУНКЦИИ y=
f(x) В ТОЧКЕ x* |
_________________ |
| 3) ФУНКЦИЯ, РАВНАЯ ОТНОШЕНИЮ ДВУХ ПОЛИНОМОВ | _________________ |
| 4) ФУНКЦИЯ R=a1x1+
a2x2+…+ anxn, МАКСИМУМ ИЛИ
МИНИМУМ КОТОРОЙ НАХОДИТСЯ ПРИ РЕШЕНИИ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
|
_________________ |
При оценке правильности выполнения заданий открытой формы, обычно используется дихотомическая шкала {0,1}. Однако в случаях, когда в одном задании проверяется более одного элемента знаний, допустимо использовать и более широкие шкалы.
Задания, где элементам одного множества требуется поставить в соответствие элементы другого множества, называют заданиями на установление соответствия. Задания на установление соответствия эффективны при самоконтроле и текущем контроле знаний. С их помощью проверяются так называемые ассоциативные знания, то есть знания о связи формы и содержания, сущности и явления, о соотношении между различными предметами, свойствами, законами. Испытуемый должен собрать ответ из элементов списка левой и соответствующих им элементов правой колонки.
Инструкция к заданиям этой формы имеет вид:
УСТАНОВИТЕ
СООТВЕТСТВИЕ:
Номер задания ставится рядом с заголовком первого столбца. Заголовки пишутся прописными буквами. Заголовок каждого столбца относится ко всем элементам соответствующего множества. Элементы должны соответствовать названиям столбцов и быть короткими. Элементы левой колонки нумеруются цифрами, элементы правой – прописными буквами. Номер и буква отделяются от элементов столбца круглой скобкой и пробелом.
На каждый элемент слева должен найтись по крайней мере один элемент справа, а каждому элементу справа должен соответствовать только один элемент слева.
Примеры:
|
ЧИСЛЕННОСТЬ ПОПУЛЯЦИИ A) постоянна B) экспоненциально растет C) экспоненциально убывает D) сначала возрастает, потом убывает E) сначала убывает, потом возрастает F) колеблется с постоянной амплитудой |
|
ЭКВИВАЛЕНТ A) logbA´ logbB B) (logbA)/( logbB) C) logbA+ logbB D) logbA- logbB E) rlogbA F) (logbA)r |
ОТВЕТЫ: 1 _____; 2 ______, 3 _______.
Строка ответов пишется посредине задания. Испытуемый пишет ответы буквами из правого столбца в соответствующих пробелах рядом с номерами.
Примеры:
|
РЕСУРС A) земля B) электроэнергия C) энергия ветра D) труд людей E) сила животных |
ОТВЕТЫ: 1 _____; 2 _____.
| ФОРМУЛА A) log2(rx) B) cеrx C) axr D) bx E) xr F) a ln x |
ОТВЕТЫ: 1 ___; 2 ____; 3 ____.
| ОПРЕДЕЛЕНИЕ A) 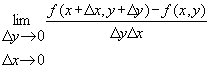 B) C) |
Оценивая правильность выполнения задания на установление соответствия, можно использовать дихотомическую шкалу: 1 за безупречно выполненное задание, 0 даже за одну допущенную ошибку. Однако можно выставлять оценки на основе более широкой порядковой шкалы: 0 –“совершенно неверно”, 1- “есть верные элементы”, 2 – “много верных элементов” или “совершенно верно”, и т.д.
В тех случаях, когда требуется установить правильную последовательность действий или слов в определениях, используются задания на установление правильной последовательности. Это более сложный тип задания в тестовой форме, в процессе выполнения которого испытуемый конструирует ответ из предложенной неупорядоченной последовательности слов.
Задания на установление правильной последовательности используются для проверки знаний хода процесса, цепочки событий, действий и операций, а также определений и понятий. Они помогают формировать у учащихся алгоритмические мышление, знание и умение. Задания этой формы полезны как в качестве средства контроля знаний, так и в качестве средства обучения.
Инструкции к заданиям этой формы имеют вид:
УПОРЯДОЧИТЕ:
или
УСТАНОВИТЕ ПРАВИЛЬНУЮ ПОСЛЕДОВАТЕЛЬНОСТЬ:
Испытуемый должен расставить в отведенных для ответов местах в начале каждой строчки порядковые номера элементов последовательности действий.
Посредством заданий этой формы можно проверять знание последовательности доказательства теорем.
Пример: =0
=0Задания на установление правильной последовательности полезны при проверке знаний формулировок утверждений и определений.
Пример:После расстановки номеров слов в этом задании должно получиться утверждение: “То, что ничего не стоит, потребляется быстрее, чем необходимо”.
Инструкция к заданию может сопровождаться необходимыми пояснениями. Название задания пишется заглавными буквами; оно декларирует, знание чего должен продемонстрировать испытуемый, причем ключевое слово в нем должно иметь именительный падеж.
Ранжируемые элементы в задании ставятся в случайном порядке. Чтобы окончания слов не служили подсказкой, их пишут в именительном падеже. Предлоги и союзы из множества ранжируемых элементов могут исключаться.
Чаще всего используется дихотомическая оценка правильности выполнения задания: 0 или 1. Однако можно применить и другое правило оценивания. Например, правильно выполненное задание оценивать 3 баллами, ошибка в конце задания снижает оценку на 1 балл, ошибка в середине – на 2 балла, а ошибка в начале – к снижению оценки выполнения всего задания до нуля.
Каждая из рассмотренных выше форм заданий может быть применена для проверки знаний. Выбор зависит от цели применения теста и от вкусов его разработчика.
Рассмотрим самые простые и необходимые процедуры статистической обработки результатов тестирования знаний и методы оценки качества теста в соответствии с классической теорией тестирования.
Обозначим через xij числовую оценку успешности выполнения j-го задания, выполненного i-м испытуемым. Результаты тестирования обычно представляются в виде матрицы {xij} с n строками и m столбцами (i=1,…,n; j=1,…,m). В практике тестирования принято, как правило, пользоваться дихотомической шкалой оценок результатов, когда множество возможных оценок состоит всего из двух элементов {0;1}: 0 – задание не выполнено, 1 – выполнено правильно. Это, конечно, не единственно возможная шкала. Расчет, однако, ведется по формулам, приведенным ниже, независимо от выбранной для оценок шкалы.
Процесс статистической обработки матрицы результатов тестирования будем рассматривать последовательно, по шагам.
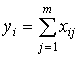 .
.Поскольку для проверки статистических гипотез, которые применяются в классической теории тестов, используют предположение о нормальном распределении суммарных баллов испытуемых, то рекомендуется исследовать распределение частот. Для сравнения распределения баллов с нормальным можно использовать любой из критериев, применяемых обычно для этой цели.
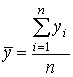 .
. 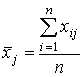 .
.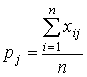 .
.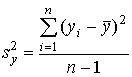 ,
,  .
.  .
.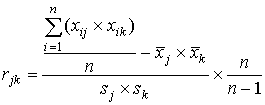 .
.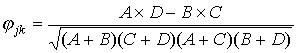 ,
, ,
, 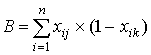 ,
,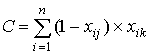 ,
, .
.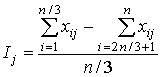
Чем больше коэффициент Ij, тем больше дискриминативность задания.
При наличии больших выборочных совокупностей дихотомических данных и нормального распределения индивидуальных сумм баллов рекомендуют рассчитывать для всех заданий бисериальные коэффициенты корреляции Вj (j=1, 2, … m):
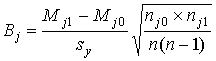
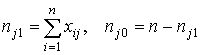 ,
,
Чтобы полученное собрание тестовых заданий можно было считать тестом, оно должно удовлетворять определенным критериям надежности и валидности.
Надежность теста r
тем выше, чем более согласованы результаты одного и того же человека при повторной проверке знаний посредством того же теста или эквивалентной его формы (параллельного теста). Согласованность результатов можно измерять коэффициентом корреляции Пирсона.
Если значения коэффициента r попадают в интервал 0,80-0,89, то говорят, что тест обладает хорошей надежностью, а если этот коэффициент не меньше 0,90, то надежность можно назвать очень высокой.
Другие, более практичные, методы оценки надежности теста, основаны на однократном применении единственной формы теста.
При применении метода расщепления откорректированную выше описанным образом тестовую матрицу разбивают на две половины, состоящие из заданий с четными и нечетными номерами. Коэффициент корреляции r1/2 Пирсона между двумя совокупностями суммарных баллов результатов сам по себе уже может служить оценкой надежности всего теста.
Оценку надежности полного теста можно делать также с использованием коэффициента корреляции r1/2, по формуле Спирмана-Брауна :
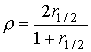 .
.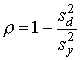 ,
,![]() - дисперсия суммарных баллов результата,а
- дисперсия суммарных баллов результата,а ![]() - дисперсия разностей между результатами каждого испытуемого по обеим половинам теста. Она вычисляется по формуле :
- дисперсия разностей между результатами каждого испытуемого по обеим половинам теста. Она вычисляется по формуле :
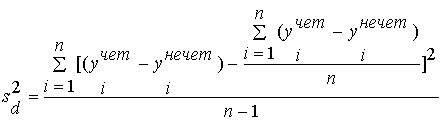
Здесь ( yiчет-yiнечет), (i=1,2,…n) - разность сумм баллов в строках с номером i субматриц с четными и нечетными заданиями.
Еще один метод определения надежности, основанный на однократном предъявлении единственной формы теста, носит имя Кьюдера-Ричардсона. Он использует данные о выполнении испытуемыми каждого задания. Коэффициент надежности Кьюдера-Ричардсона вычисляется по следующей формуле:

Показано, что такой коэффициент равен среднему арифметическому значений коэффициентов надежности, найденных по методу расщепления при всех возможных разбиениях теста.
Чем выше показатель надежности, тем меньше стандартная ошибка измерения индивидуального результата. Показатель надежности можно использовать для построения доверительного интервала, в пределах которого с выбранной вероятностью Р находится истинное значение оценки знаний испытуемого: ![]() , где tP – значение статистики Стьюдента, найденное для выбранной вероятности P, когда число испытуемых равно n.
, где tP – значение статистики Стьюдента, найденное для выбранной вероятности P, когда число испытуемых равно n.
Валидность теста показывает, насколько хорошо тест делает то, для чего он был создан. Определить коэффициент валидности теста – значит определить, как выполнение теста соотносится с другими независимо сделанными оценками знаний испытуемых. Для определения валидности требуется независимый внешний критерий, то есть оценка эксперта (преподавателя). За коэффициент валидности принимают коэффициент корреляции результатов тестовых измерений и критерия. Если экспертная оценка знаний испытуемых, полученная независимо от процедуры тестирования, представлена числовой последовательностью Y1,Y2, …, Yn, то коэффициент валидности теста может быть рассчитан по формуле:
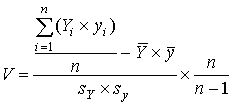 ,
, ,
, 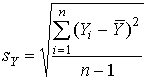 .
. Из двух тестов, предназначенных для одной и той же цели, более эффективен тот, который быстрее, дешевле и качественнее измеряет знания данной группы испытуемых.
При подготовке материала использованы следующие литературные источники: