Постановка задачи предполагает наличие математической модели иссле¬дуемой или проектируемой системы, и модель эта зависит от п параметров а1 . . ., аn. Слова «математическая модель» означают, что имеются формулы, позволяющие по заданному набору а1 . . ., аn вычислить любые интересующие нас характеристики системы. Сами а1 . . ., ап могут быть естественными физическими величинами, например, массами ра¬диусами, жесткостями и т. п., или, если единицы измерения этих величин фиксированы, могут считаться безразмерными. Если функционирование системы описывается дифференциальными уравнениями, то в качестве параметров можно выбирать коэффициенты или начальные значения этих дифференциальных уравнений.

Пространство параметров. Пространством параметров называется n-мерное пространство, состоящее из точек А с декартовыми координатами (alt . . ., ап). Таким образом, каждой точке А пространства параметров соответствует конкретный набор параметров (а,, ..., а ) и наоборот.

Как правило, проектировщики могут указать разумные пределы изменения каждого из параметров, которые мы будем называть параметрическими ограничениями

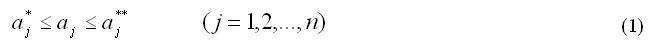
Ограничения (1) выделяют в пространстве параметров параллелепипед (рис. 1). П = {А | (1)}

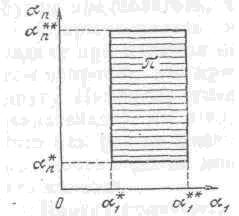
Рис. 1 – Параллелепипед П в пространстве параметров

Функциональные ограничения. Кроме параметрических ограничений обычно в условия задачи включаются функциональные ограничения.

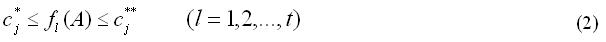
Здесь f(А) — некоторые функции от параметров А = (а1, . . ., аn). Они могут быть заданы явно. Но если, например, функционирование системы описывается диф¬ференциальными уравнениями, то f(А) часто представляют собой функционалы, зависящие от интегральных кривых этих уравнений.

Обозначим через G подмножество параллелепипеда П, состоящее из точек А, удовлетворяющих ограничениям (2) (рис. 2.2):

G = {А | (1),(2)}

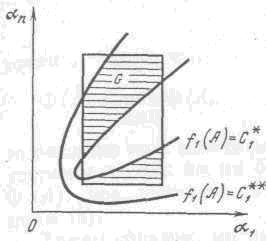
Рис. 2 – Множество G в параллелепипеде П

Критерии качества. Критерием качества называется характеристика системы, которая связана с ее качеством монотонной зависимостью. Иными словами, при прочих равных условиях система тем лучше, чем больше (меньше) критерий. Для простоты записи мы всюду в дальнейшем будем предполагать, что все заданные критерии Ф1 (А),. .., Фк (А) желательно уменьшить:

Следовательно, чем меньше Фv(А), тем лучше.

Формально, любой критерий можно привести к такому виду, заменяя, если это нужно, Фv на 1/Фv или на -Фv

Рис. 3 Множество допустимых точек D