|
ИССЛЕДОВАНИЕ АЛГОРИТМОВ ЦИФРОВОЙ ФИЛЬТРАЦИИ СИГНАЛОВ СИСТЕМЫ КОНТРОЛЯ КОНЦЕНТРАЦИИ МЕТАНА Краснокутский В. А., Гомозов О. В. Донецкий национальный технический университет, ФВТИ, ЭВМ kras@cs.donntu.ru blackswanny@gmail.com
Abstract
Krasnokutsky V.A, Gomozov O.V. Research into digital filtering algorithms of methane concentration control system signal. We research into FIR and IIR algorithms for analysis of signals receiving from methane concentration sensors. We propose algorithm that can be realized on DSP processors.
1. Постановка задачи
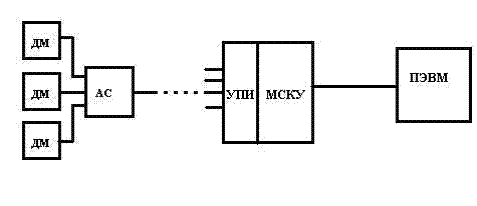
Рис.1. Схема аппаратно-программного комплекса КАГИ Основной частью системы является УПИ и МСКУ,который способен получать и обрабатывать информацию от АС, находящегося в шахте и снимающего показания с 3-ех датчиков в виде высокочастотных сигналов, после чего эта информация попадает в ПЭВМ для дальнейшего анализа. Для фильтрации этих сигналов применяются аналоговые аппаратные полосовые фильтры. Они настроены на частоты 14КГц, 20КГц и 26КГц, каждая из которых отвечает за состояние одного из датчиков. При аварийности (превышении концентрации метана отметки в 2,5%) эти сигналы начинают модулироваться частотой 3-5Гц. Сигналы передаются по единому проводу, тем самым наблюдается их наложение, кроме того присутствует сигнал в 1КГц для работы телефонной линии, а также сильные шумы и ослабление информационных сигналов, так как расстояние между АС и УПИ может достигать 11 км, поэтому так же возможен обрыв линии и влияние сильной помехи. При фильтрации этих сигналов используется аналоговые методы на основе полосовых аналоговых фильтров. Кроме того с помощью фильтра нижних частот из сигнала АС выделяется постоянная составляющая тока, фиксирующая значение концентрации метана. Схемы модулятора-демодулятора осуществляют гальваническую развязку по постоянному току и формирование на выходе напряжения, определяющего величину концентрации метана. После фильтрации формируются дискретные сигналы, которые при помощи блоков МСКУ обрабатываются, преобразовываются и попадают в ЭВМ, которой управляет оператор и видит ситуацию в шахте, принимая соответствующие решения. Физически эти схемы являются отдельными платами(по одной на один АС) и устанавливаются в стойки УПИ. И таких плат может быть несколько десятков. Аналоговые фильтры являются устаревшими и сложными устройствами. Они требуют наладки при изготовлении и постоянной настройки при использовании. Кроме того у них есть множество неразрешимых недостатков:
Выше перечисленное приводит к удорожанию стоимости производства и обслуживания таких систем, усложнению технологического процесса, ухудшению показателей системы. Использование цифровых систем обработки сигналов (ЦОС) может решить эти проблемы. В настоящей статье исследуется один из возможных подходов к решению задачи обработки сигналов от АС, основанный на рекурсивных БИХ-фильтрах[1].
2. Исследование алгоритмов ЦОС
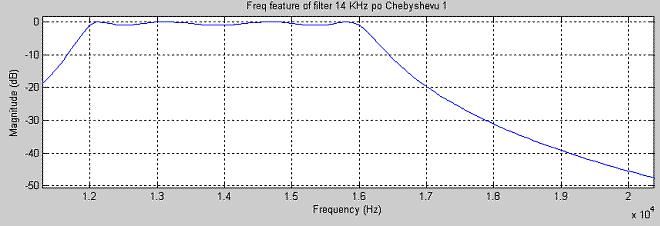
При расчете фильтра основными параметрами были уровень затухания в полосе задерживания и пульсации в полосе пропускания. Необходимо было достичь затухания соседних с фильтруемой частот до незначительных величин. Поэтому для пульсаций был установлен минимально допустимый уровень в 1Дб (1,12 раза), а для затухания был принят уровень в районе 40Дб (100 раз). Значения полос брались в диапазоне +/- 3КГц(+/-2КГц для полосы пропускания) от фильтруемой частоты, как срединные между двумя соседними частотами – оптимальный случай. При этом необходимо было учитывать порядок фильтра, который возрастал при увеличении уровня затухания, что было невыгодно для дальнейшей реализации. В результате исследования при прочих одинаковых параметрах лучшие характеристики по подавлению сигналов (наихудший случай 36,8 Дб - в 70 раз меньше) были у фильтра Чебышева 1 рода, что показано на рис. 1.1-1.3. При этом был получены минимально возможные фильтры 4 порядка (полиномы 9-степени).
1. 1 АЧХ фильтра 14КГц Чебышева 1 рода
1. 2. АЧХ фильтра 20КГц Чебышева 1 рода
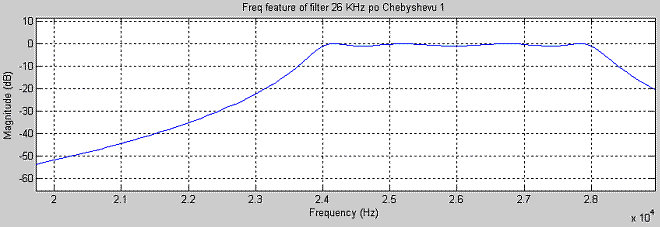
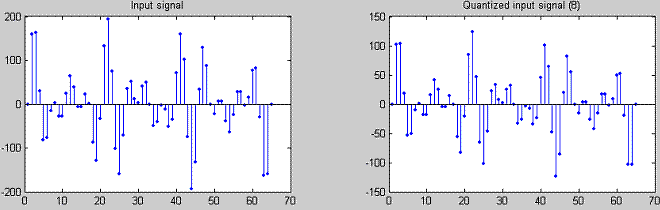
1. 3. АЧХ фильтра 26КГц Чебышева 1 рода Система моделирования MATLAB по умолчанию работает с 64-разрядными данными, с плавающей запятой, и проводить моделирование в этом представлении было бы некорректно. Для этого были проквантованы данные как для АЦП, так и для самого 16-разрядного процессора, использовался формат с фиксированной запятой, что вполне удовлетворяет требованиям, кроме того процессоры с такой арифметикой дешевле. Эффекты квантования влияют на погрешность вычислений, точность представления данных и возможные переполнения, для чего были проведены эксперименты по влиянию этого параметра на характеристики системы и выбор оптимально допустимых. Для исследования разрядности АЦП моделировалась ситуация квантования с разрядностью 8,10,12 бит (стандартные для многих АЦП), и дальнейшего восстановления (деквантования), с целью обнаружения погрешности. В результате экспериментов было выявлено, что 8-битовых АЦП вполне достаточно для достоверного представления данных, что показано на рис. 2.1-2.2, и является более дешевым вариантом, чем 10 и 12 разрядов.
2. 1 Входной и кодированный сигнал (8 разрядов)
2. 2 Восстановленные из кодированных сигналы (8 разрядов и 12 разрядов) Для определения формата данных, а именно, количества разрядов , отведенных под целую и дробную часть были проведены опыты по обнаружению переполнений. Чем меньше дробная часть, тем хуже точность, но при её увеличении могут появиться переполнения, приводящие к ошибочным результатам. Были проведены исследования, оптимальным является 9 разрядов для дробной части и 7 для целой. В связи с особенностями реализации фильтров, они не сразу пропускают информативный сигнал.Так как сначала предыдущие отсчеты отсутствуют (нулевые). Время реакции условное , в котором предполагается, что алгоритм работает быстрее, чем АЦП формирует отсчеты. В результате при частоте дискретизации в 128КГц время реакции фильтров следующее: 0.641 мс для 14КГц, 0.570 мс для 20КГц, 0.516 мс для 26КГц (рис. 3). Как видно, чем выше частота , тем быстрее формируются необходимые отсчеты и срабатывает фильтр.
Рис. 3. Время реакции фильтров Для расчета помехоустойчивости к общему сигналу “примешивалась” помеха и проводилось множество опытов для достоверности результатов, после чего была определена максимально допустимая помеха в 5% от амплитуды информативного сигнала(при этом обнаруживается более 95% информации). Испытания проводились с использованием равномерно распределенной нормализованной помехи 20 раз при 256 отсчетах ,а также контрольные 10 раз при 512 отсчетах для подтверждения результата. Для обнаружения наличия частоты в отфильтрованном сигнале среди прочих других был выбран метод “сумм периодов”. При этом для каждой фильтруемой частоты создается “образ” периода, как бы снятый с такой же частотой дискретизации, как образец для сравнения с отсчетами текущего периода. При этом сравнению подвергаются два признака
Такой метод показал себя лучше других и при прочих равных параметрах производил обнаружение 97-99% периодов при средней погрешности в 6%. Наиболее оптимальная частота дискретизации 128КГц, так как даёт минимально возможное количество отсчетов на период для правильной работы этого алгоритма (5 отсчетов для 26КГц, 7 – для 20КГц и 10 для 14КГц). Данная программа расчета и моделирования систем цифровой фильтрации для анализа состояния рудничной атмосферы может быть использована как программа-прототип для разработки аналогичной для работы процессора ЦОС. Заключение В результате моделирования системы, проведенного в MATLAB, были определены параметры алгоритма цифровой фильтрации, исследованы нестандартные ситуации и рассчитаны предварительные параметры системы, на основании которых может быть выбран процессор ЦОС, АЦП и другие необходимые элементы. Полученные результаты говорят о том, что в этой системе могут быть применены дешевые 16 разрядные процессоры, ПЛМ и другие аналоги ,а также промышленные АЦП. Применение алгоритмов цифровой фильтрации сигналов и соответствующих цифровых компонентов в данной системе позволяют:
Список литературы
|